Maxwell's Fields

Example 2: The Lorentz Force

The Question:

This shows two wires, A and B, each carrying currents pointing up.

• Remember! That the current is up, means that the actual charge carriers–negatively charged electrons–actually move down.
• But! We can pretend that these currents consist of positively charged particles, say protons, which would move in that up direction. While that's not what happens in actual wire-carrying-currents, it is a perfectly fine particle accelerator "current" of protons or currents in the upper atmosphere of cosmic rays impinging from outer space. "Currents" mean more than what's coming out of the wall in your house.

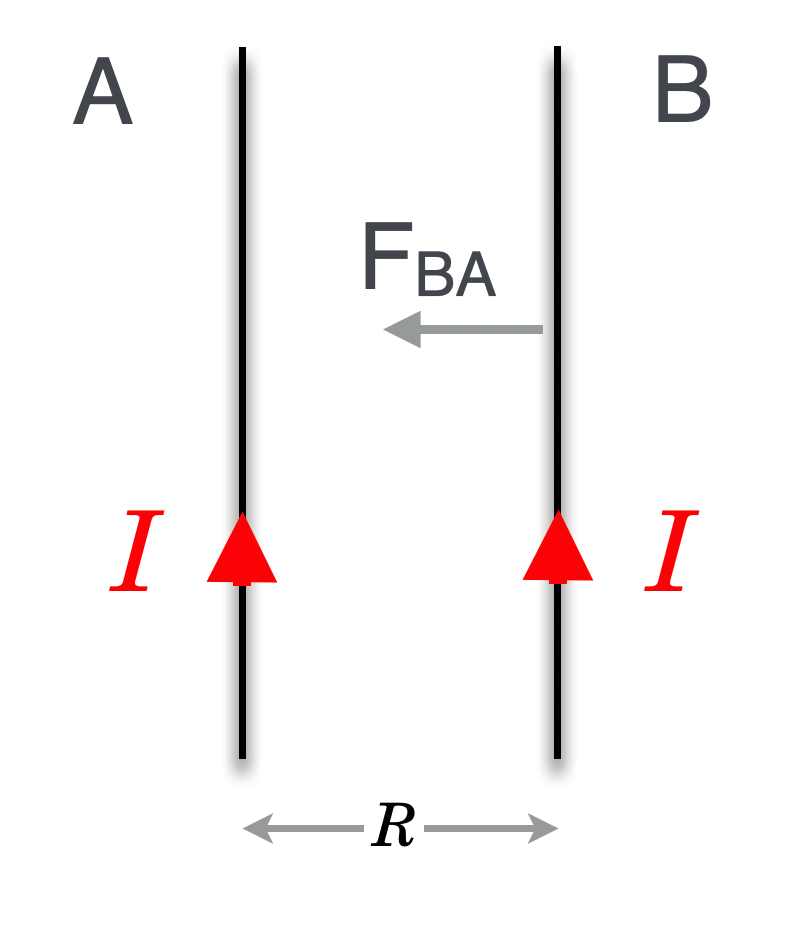
We saw that the wires would feel a force of attraction and physically move. Now we're going to understand why. Here we're concentrating on the force that wire B feels due to current A, $F_{BA}$.

Explain the force between two current-carrying wires in terms of the Lorentz Force.

The Answer:

First, let's recall the magnetic field produced by current A as it would extend to the position of wire B.

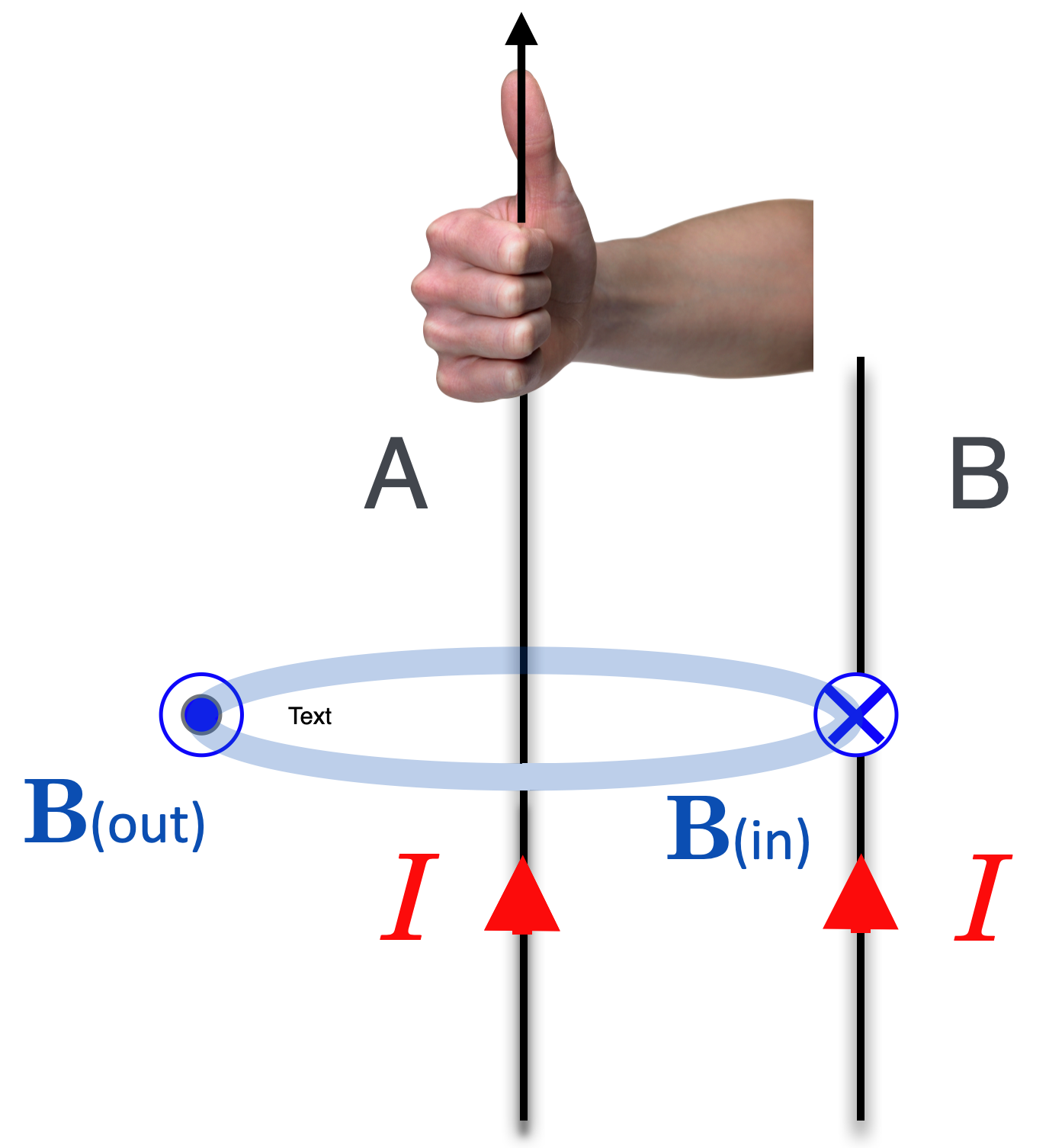
Here we see that the B field due to current A is a set of concentric circles around the wire, one field line of which is drawn at the position of wire B. Remember that the circle-dot suggests a vector pointing out at you and the circle-X is a vector pointing in, away from you. My right hand shows you the direction of that B field.

Let’s look at the situation by peering down wire A from above. We’d see this:

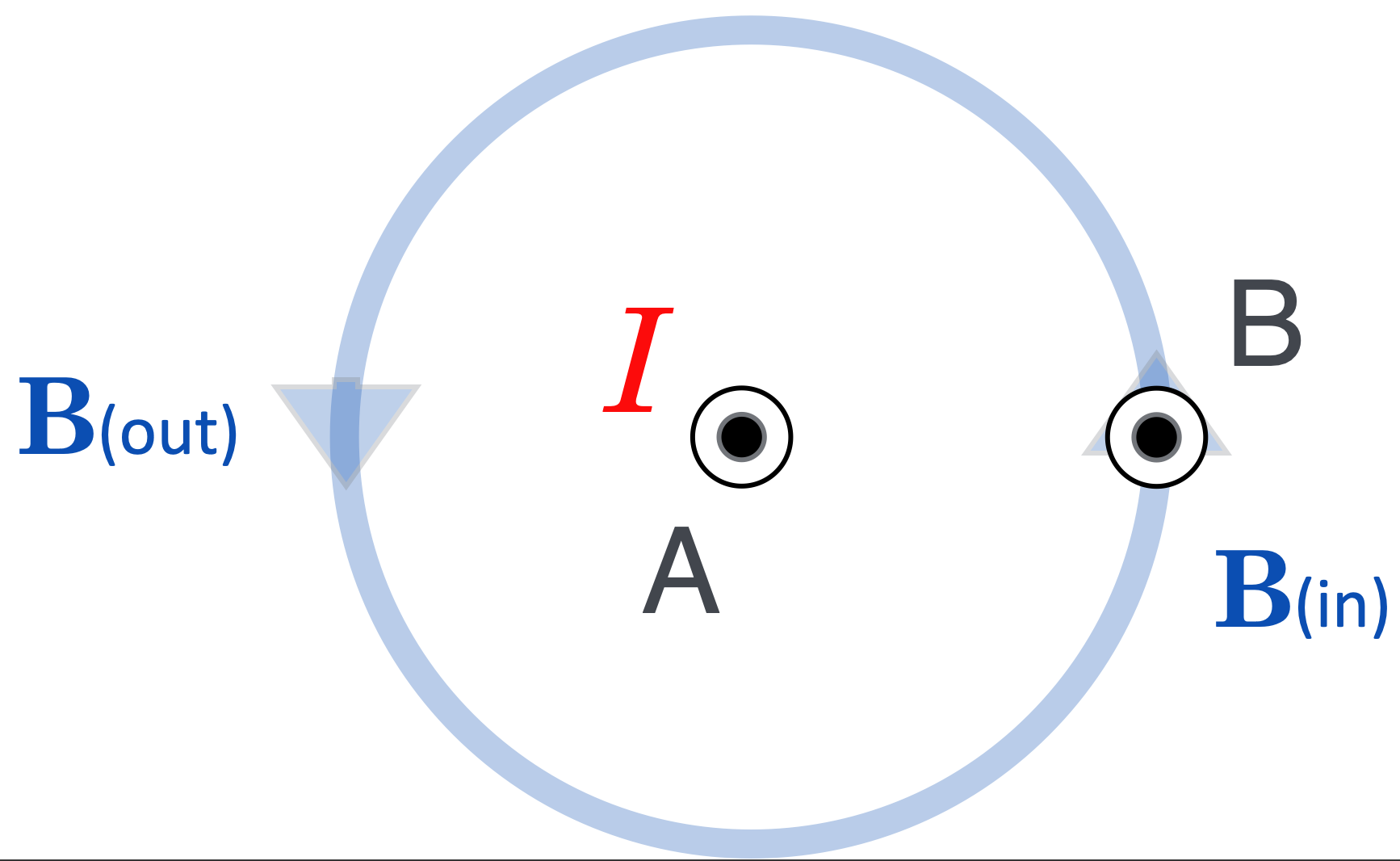
Now, let’s get rid of wire A and leave only the magnetic field that it produces. As far as wire B is concerned, all it knows about is that field and it knows nothing about where it comes from.

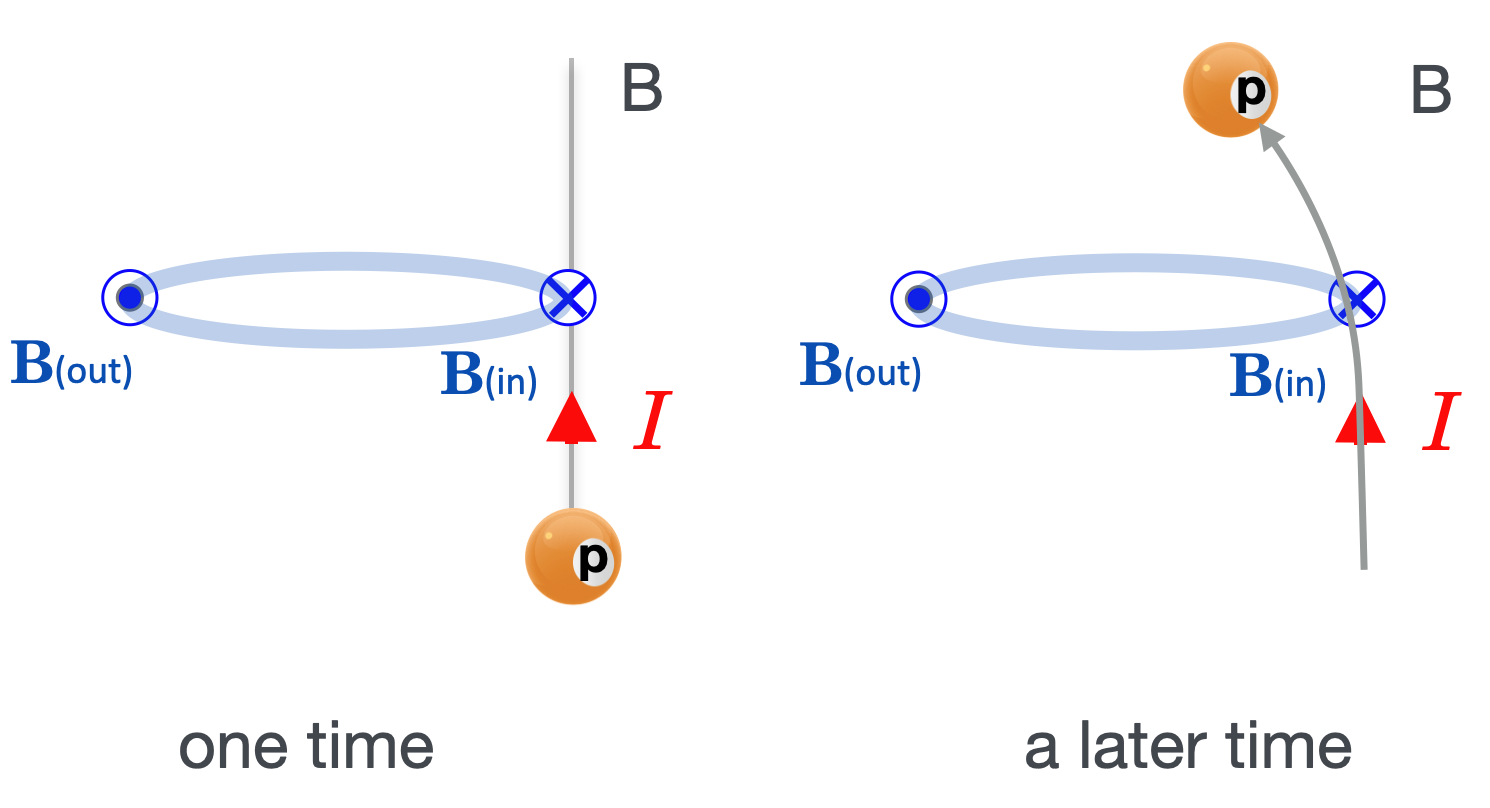
Further, let’s replace the current in B with charged particles, in this case, imagine a current of positively charged particles–protons. So following one of those protons at two different times:

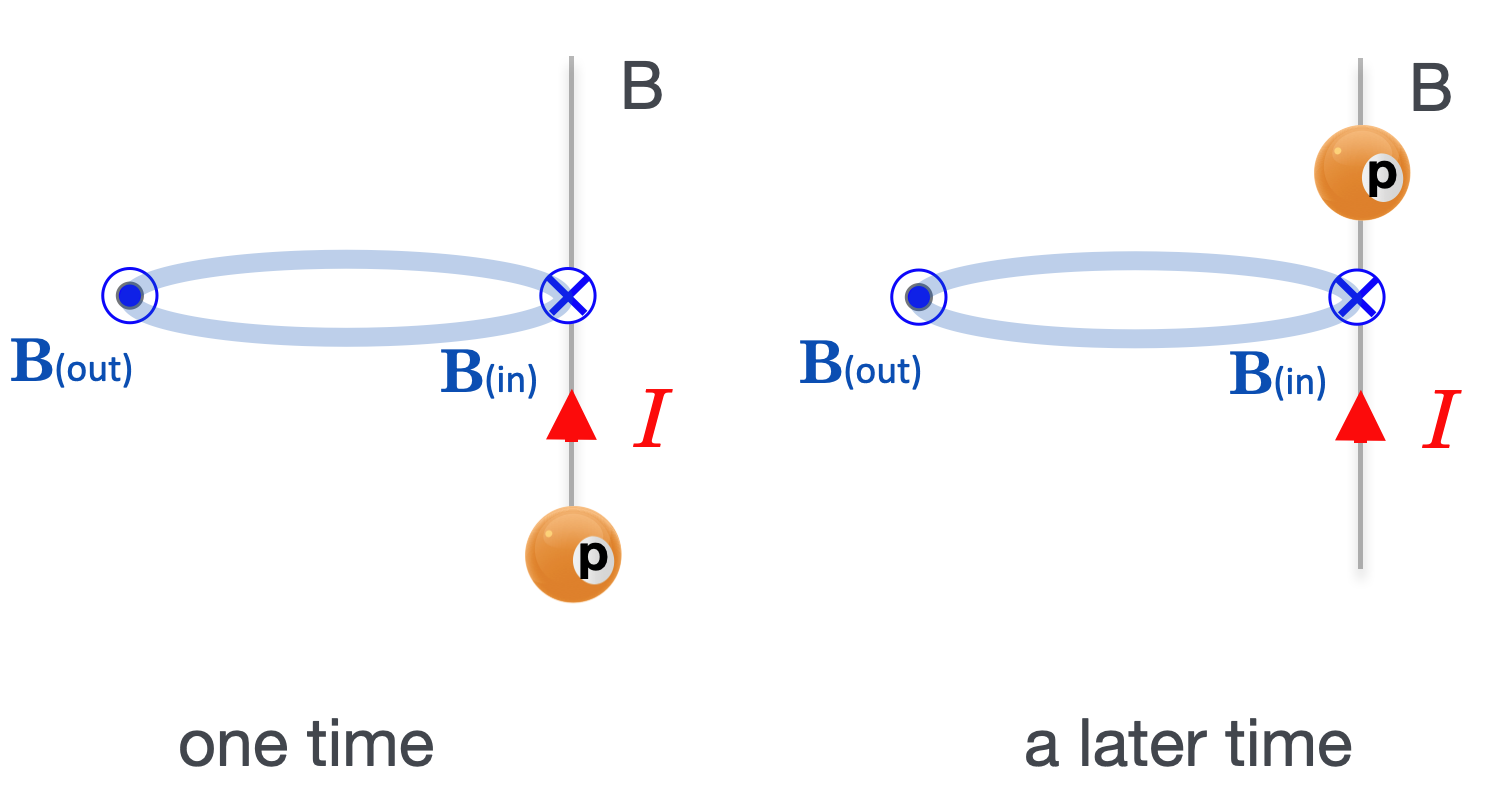
So the protons moves in time and space, and so it has a velocity.

But wait, that’s not what we see, right? Wire B actually physically moves to the left, towards wire A. In terms of our proton-current, its trajectory has to bend:

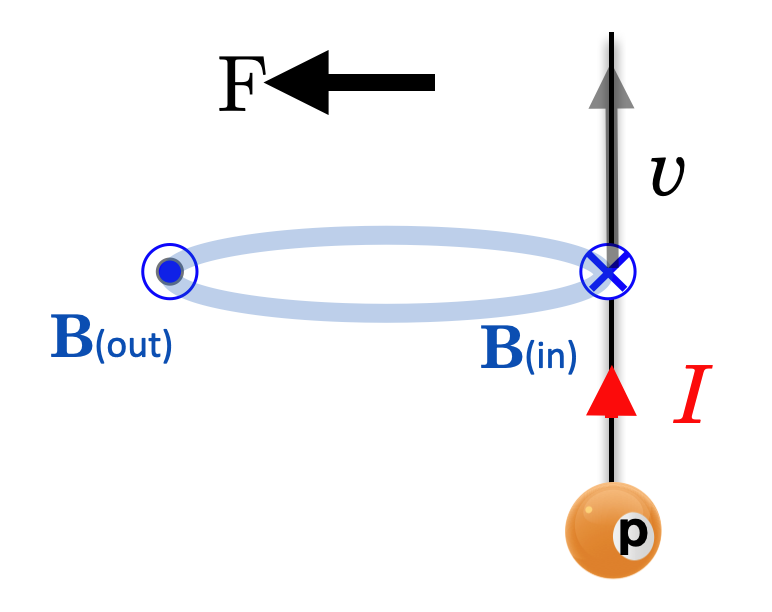
That's what a magnetic field does:

A magnetic field bends the trajectory of a moving charged particle.

As the sketch shows, the trajectory is straight up…until the proton enters a region where there’s a magnetic field and it reacts by bending. Once it leaves the magnetic field influence, it continues on in a straight line…just like Newton would have insisted.

So the direction of the velocity and the direction of the B field are key. A force results when these two vectors are not parallel to one another–and its maximum when they are perpendicular, as in our example:

What’s complicated about this is figuring out the direction of the bend and this example helps us to figure out a general rule. Let’s look down from the top again:

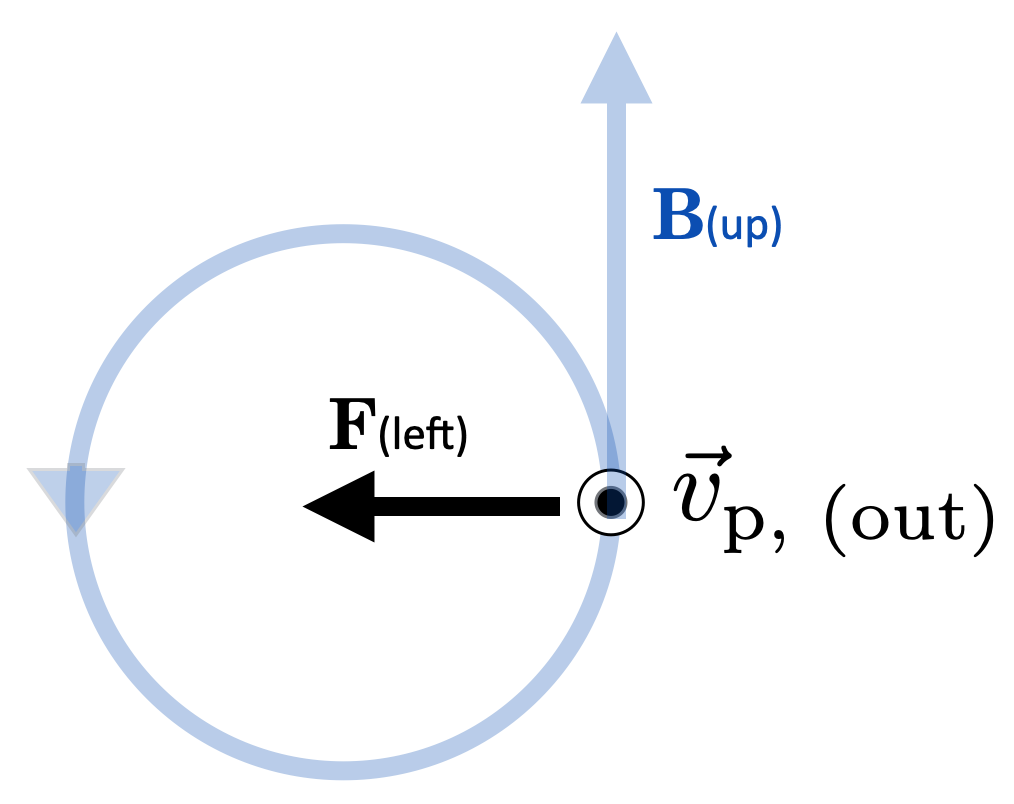
Here, the proton “current” is coming out at you, so its velocity is “out.” The magnetic field vector is up, and we know from the bending that the force on the proton is in towards the center of the circular B field (towards wire A).