Collisions
Example 2: The Stop Shot
In our fake “momentumunits” let's invent an example and follow it through. If you can do this kind of thing, then you're in good shape to understand any scattering process.
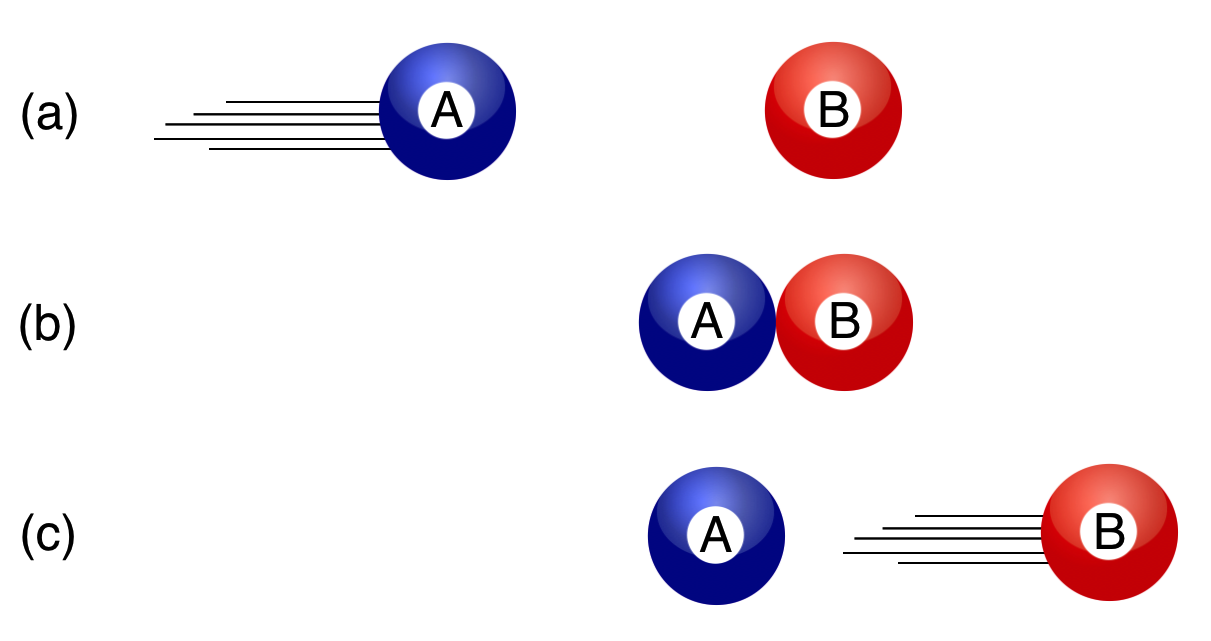
- We'll make the initial momentum of the cue ball to be "12," in our fake units the momentum of at (a) is:
- B is initially sitting still at (a), so the initial speed of the B is zero, .
- The mass of each ball is 6, so
Now for a bunch of questions:
- What is the initial momentum of the B ball?
- What is the initial speed of A?
- What is the total momentum of the entire initial state?
- Using your experience and the video, what is the final momentum of A, ?
- What's the total momentum of the entire final state?
- From our observation and momentum conservation, what is the final momentum of B, ?
- From our observation and momentum conservation, what is the final speed of B, ?
Before looking at momentum conservation, we can deal with the first three questions easily:
Answer 1. If the B ball is stationary, then its velocity is 0 and so its momentum is 0, .
Answer 2. If the intial momentum of A is 12, then the speed of A we can get easily from the definition,
Answer 3. The total momentum of the "entire intial state" is just the sum of all of the individual momenta of all of the objects in the initial state. Let's call that without any A or B label. In this case,
Answer 4. Our experience is that in the final state the beam ball stops, so .
Answer 5. If we name the total momentum of the entire final state to be , in solidarity with the entire initial state momentum of , momentum conservation says that
that if then as well.
The final two questions require that we make use of momentum conservation. Let's set up a table (which you might do in your head some day) and you can think of balancing things. Remember, conserving momentum here means enforcing:
Here's the table in which we need to supply the missing in the right hand column:
| Before (initial state) | After (final state) | |
|---|---|---|
| total | ||
| A | ||
| B | ||
| sum to: |
In the Before column we've listed what we knew. We need to fill in the After column. Let’s take them one at a time:
- What is ? The first line is easy since we've already done it in Answer 5: momentum conservation insures that z has got to be the same as the initial state's total, so .
- What is ? Our experience tells us that when we strike B with the A that the A suddenly stops dead (Answer 4.) and B jumps forward. So our experience and the video would tell us to put in zero for the final momentum of A, so .
- Answer 5: The entire final state momentum, from momentum conservation, is also 12.
- Answer 6: What is ? Of course it's 12 from momentum conservation and that's the answer to question #4.
Answer 7: that question asks about the speed of B after the scattering event. Since the mass is 6, and the momentum is , then we can see easily that and B goes scooting away with the same speed as A had before the collision.
So this next table completes our understanding of this collision, using experience as our guide.
| Before (initial state) | After (final state) | |
|---|---|---|
| total | ||
| A | ||
| B | 12 | |
| sum to: |