A little deeper

Fraction of kinetic energy lost.

So we found that the initial state’s kinetic energy is (A, in the previous labeling):

$K_0=35.1$ J

Then, after Herman bravely catches that ball, the combined kinetic energy of the both of them (C) is:

$K=0.1$ J

That’s a fractional reduction of:

$\Delta K/K = (K_0 - K)/K_0 = (35.1 - 0.1)/35.1 = 35/35.1 = 0.997. \nonumber$

More than 99%!

This situation is also straightforward to model for our $A+B \to C$ collision and I’ve got a graph for that solution.

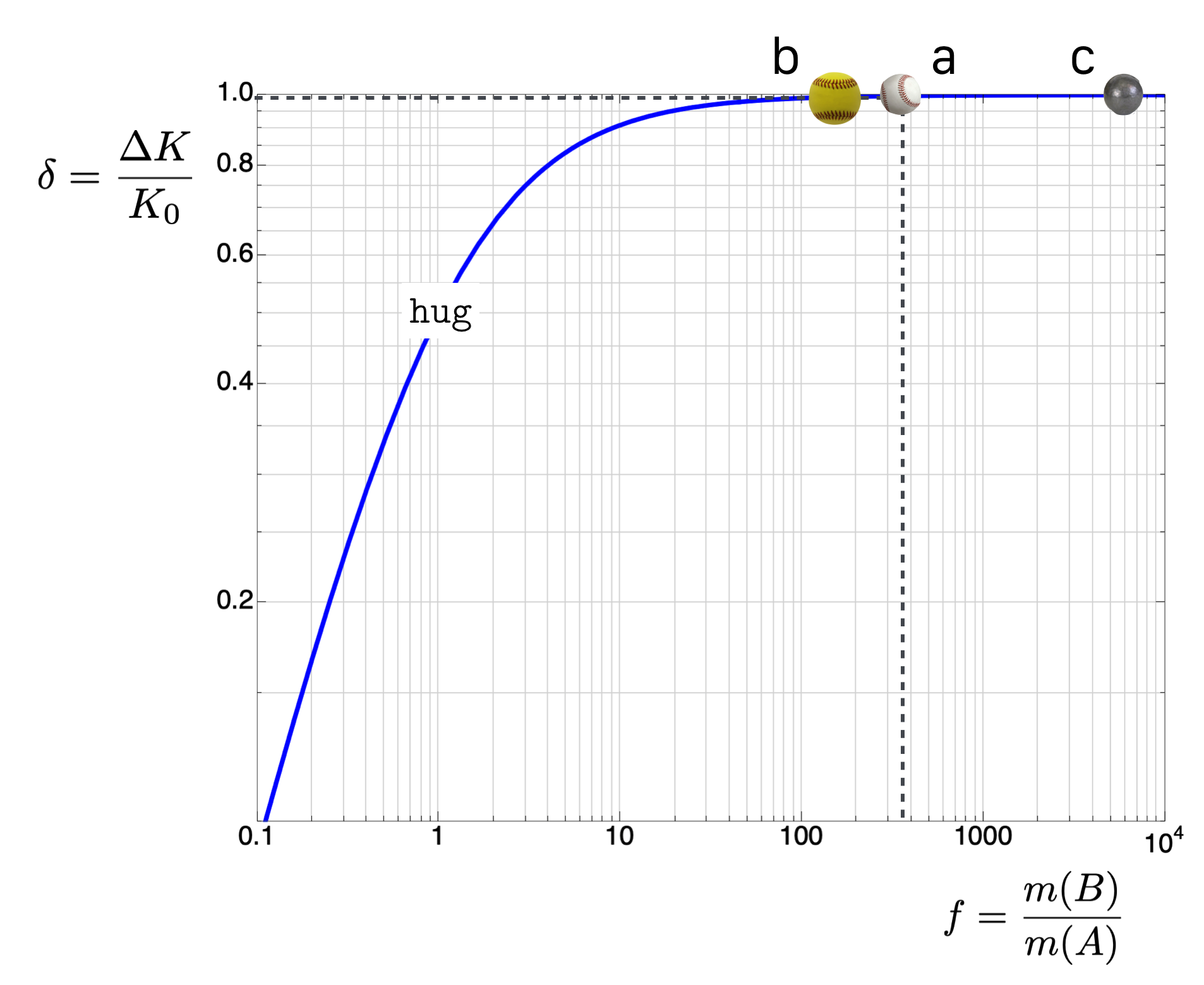
Let’s define a fraction of masses, $f$:

• $f \equiv m(B)/m(A)$, the fraction of Herman’s mass divided by the baseball’s mass,

and a new quantity, $\delta$:

• $\delta \equiv \Delta K/K$, the fraction of kinetic energy that is lost.

This graph represents any $A+B\to C$ collision. The baseball collision with Herman is shown, as are three other collisions.

What if the masses are the same? Like for twin sisters when Hannah runs towards Emma and they hug? Then $f=1$ and we’d find that the fractional kinetic energy lost by Hannah is 0.5

Remember for this curve, a smaller mass is to the right. As we can see, for small masses, essentially all of the kinetic energy is lost in a $A+B \to C$ collision. Likewise, as the masses of the beam and the target approach one another, the closer the kinetic energy loss becomes to 0.5. So from the graph, that affectionate-sister-collision will cause half of the enthusiastic sisters original kinetic energy to disappear.