Energy

Example 3: that complicated stop shot problem.

The Question:

Remember the stop shot fiasco. You’ve all seen it in real life and here it is in unreal life:

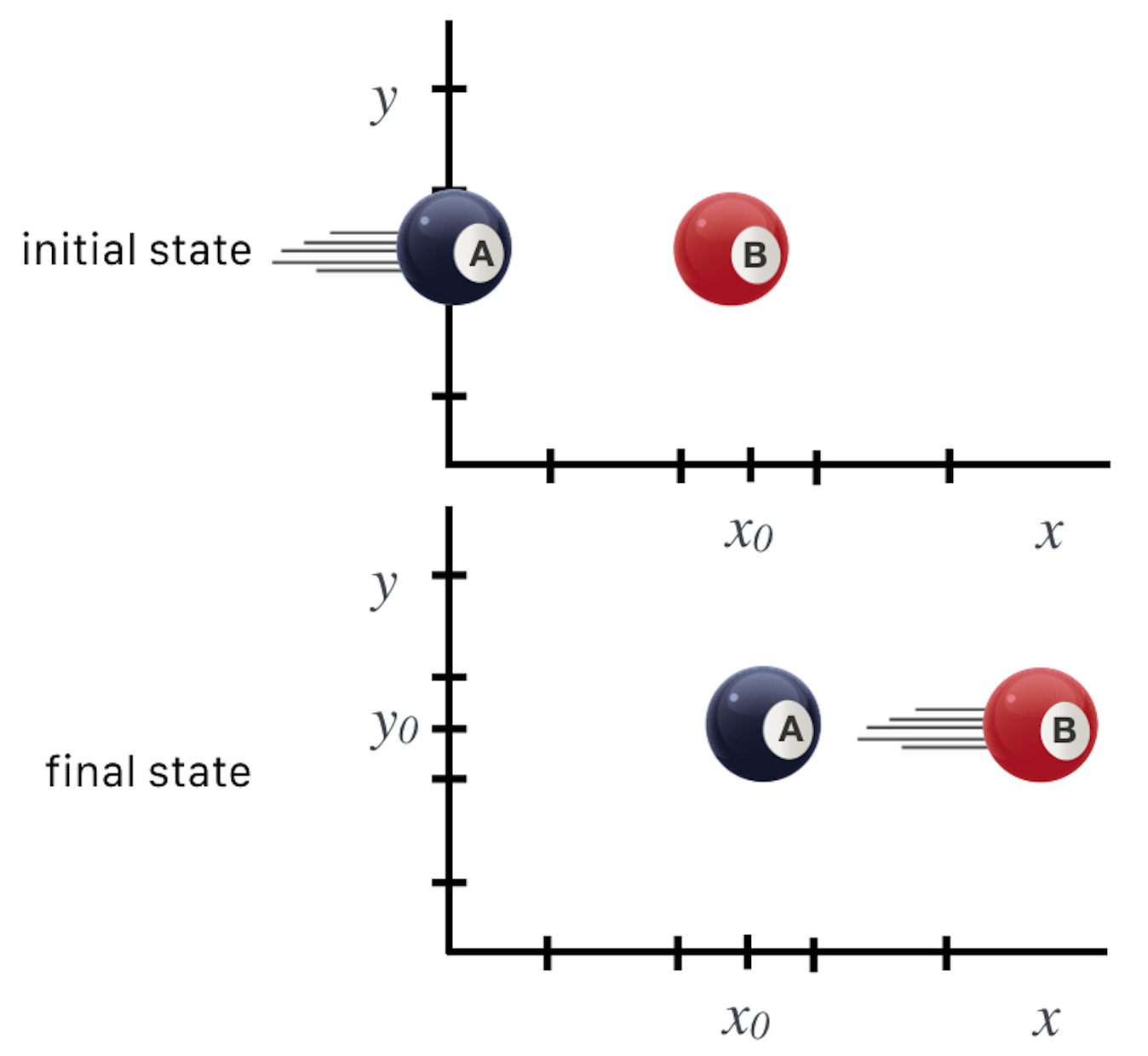
The scenario unfolds top to bottom in the figure. B is sitting there and A is heading toward it. They collide and A stops dead and B continues forward. The momentum of A has been transferred to B. Completely, if it’s an elastic collision.

But when we used momentum conservation to solve for the final velocity of B, we got something that doesn’t match what the world does:

We found that

Why is this a disaster? What we expect is that $v(B)=v_0(A)$ but that’s not what this says. It permits the final velocity of B to have a range of values somehow shared with the final velocity of A.

So here’s the question: what happens if we now insist that kinetic energy also be conserved?

The Answer:

Now, let’s include the Kinetic Energy relationship for this particular situation (remember that this notation is that $v_0(A)$ stands for the initial velocity (the 0) for object A:

In the first line I have included the fact that B in the initial state is sitting still, so it has no kinetic energy. In order to get the second line I canceled out the equal masses and the common factor of $\frac{1}{2}$.

We still have the equation that expresses momentum conservation:

In Equations 2 and 3 we have two equations with one known ($v_{A,0}$) and two unknowns ($v_A, v_B)$ to solve, which can be done in a variety of ways (remember?). You always have to keep track of what you’re looking for. Here, it’s the final velocities.

If you do the simple algebraic-gymnastics to eliminate the $v_A$ between them you get the result:

which is precisely what your experience tells you. There’s another route to insight. If instead we eliminate $v_{A,0}$ then we find:

So, either one or the other of the final velocities must be zero. One of these solutions doesn’t make any physical sense. For example, if the target ball (B) is solid, then the target ball can’t just fly right through it as if it were not there, so $v(B)$ cannot be zero, it must be something else. That means, that $v(A) = 0$ and going back to Equation 1 we see that:

which is what we expected: $v_2=0$. That's nice.

Here’s a video of the actual solution of the two above situations. It’s about 8 minutes long and is designed for you to write along if you want to.