A little deeper

Centripetal Force.

The pull on the rope for the ball swinging overhead is felt by your hand so that rope needs to be pulled by you toward the center of the circle.

Here’s how Newton explained this. The next figure shows the view of the ball from over head. In order to go in a circle the ball needs to move from point A to point B, and on to C, D, and E and then all over again.

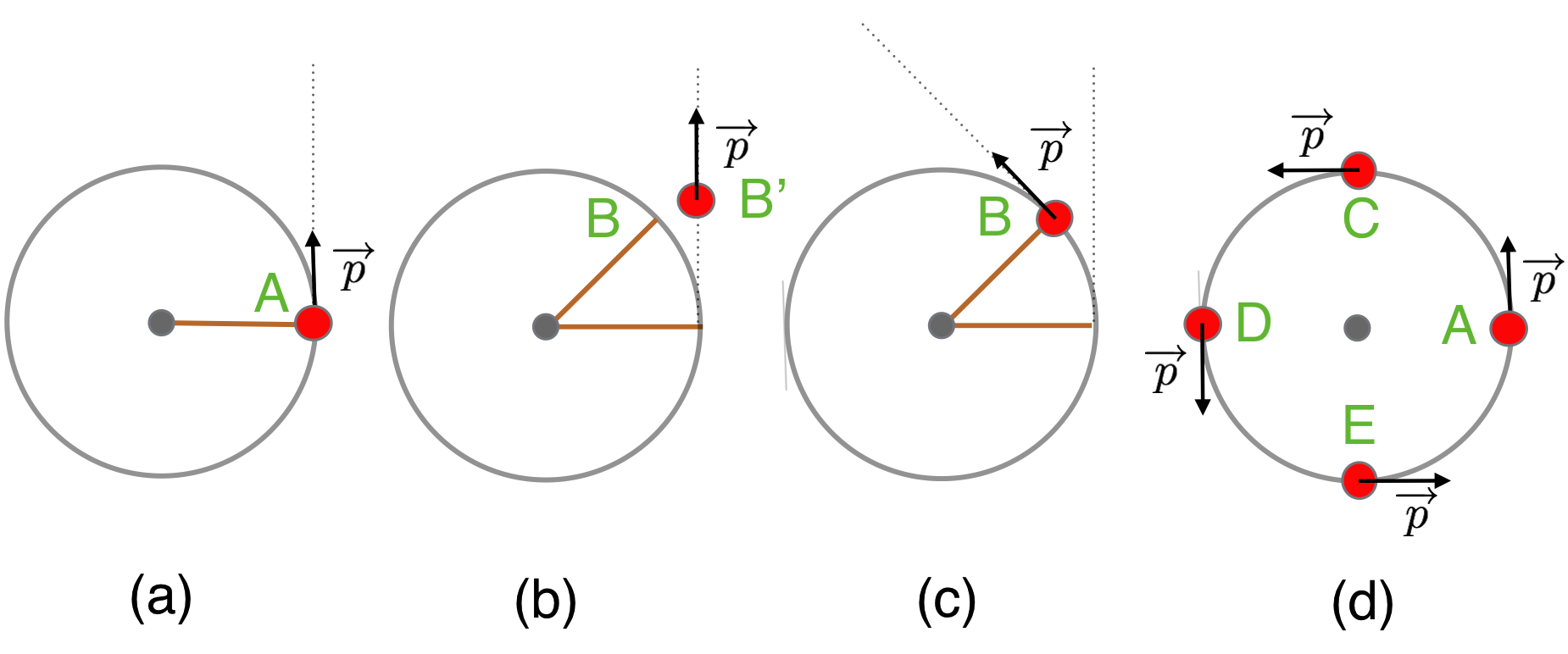A ball going in a circle from overhead at successive times, labeled (a), (b), (c), and (d). The motion is uniform, so the speed around the circle is unchanging which is reflected in the fact that the momentum vector lengths are all the same.

Since the speed is constant, the momentum vector has a constant length, but because the motion’s direction is around a circle (“not straight”!), the momentum vector is tangent to the circle at all points around the path. Newton’s brilliance was to explain this using his three laws and some geometry. Let’s deconstruct this a bit:

The ball starts at A in (a) and needs to go to B. Newton reasoned that the ball would “like” to go straight, on to point B’ (like Ira’s apple) but that the rope tugs it back to point B in (c). So the ball goes a little, gets tugged back, goes a little further, gets tugged back, and so on. These little tugs were in his mind acting all around the circle, which in the limit of being infinitesimally spaced create a continuous, circular trajectory. This notion of “infinitesimal” was kin to the habit of mind he was developing in the invention of calculus.

But let’s carry this further. Since the momentum at, say A, is different from the momentum at, say C (because the direction is different), even though the magnitudes are the same, there is still a changing momentum, a non-zero $\Delta \vec{p}$. If there’s a change in momentum of any kind, there’s a force:

Let’s see what he found.

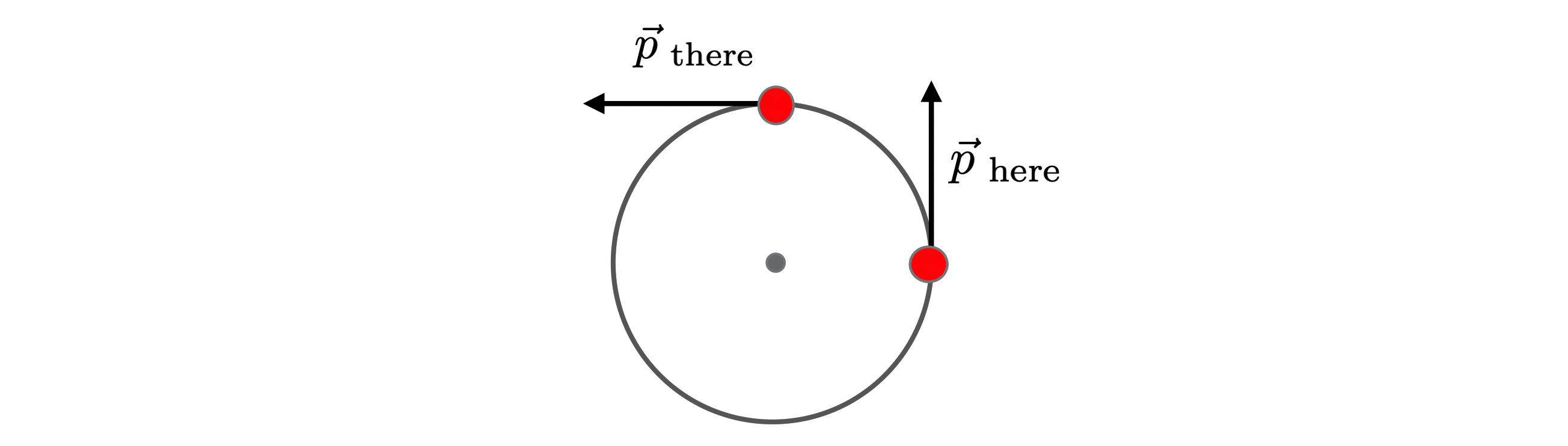This figure shows two strategically placed points on the circle “here” and “there” and the corresponding momenta of the ball associated with each point, $\vec{p}_{\text{here}}$ and $\vec{p}_{\text{there}}$

The numerator of the force relationship is the difference:

which can be constructed here from our rules about subtracting vectors described in the Mathematics lesson.

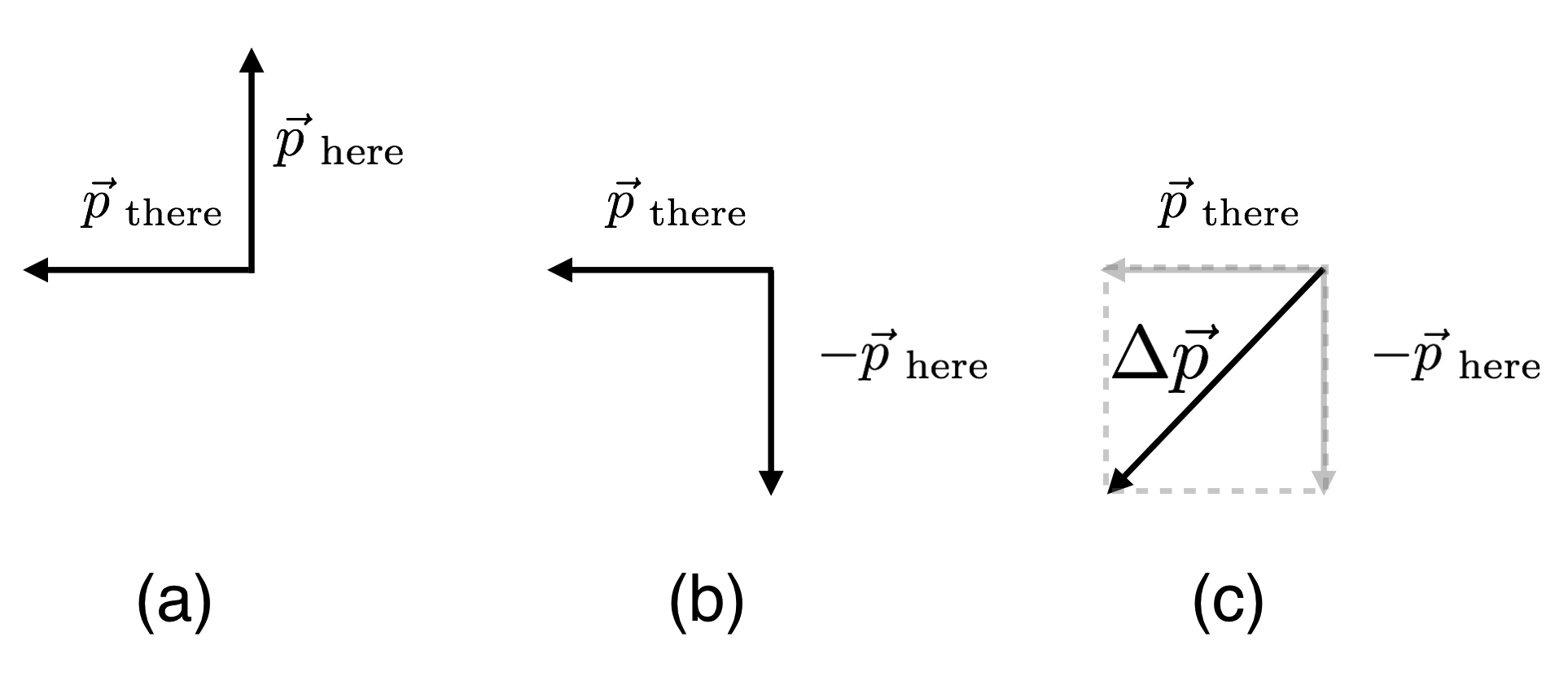The here and there vectors moved around in order to create the difference. (a) shows the two vectors translated to be together. Remember that subtraction of vectors is the same as the first vector plus the negative of the second, which is shown in (b). The resulting sum is in (c).

That difference is labeled $\Delta\vec{p}$ points very close to the center of the circle!

This was his brilliance. If the “here” and “there” points were closer and closer to one another, then the difference would point closer and closer to the center.

So like we knew all along, the rope is what causes the ball to go in a circle, the combination of Newton’s First law with his Second law, and the crucial recognition that momentum is a vector, leads to the demonstration of the force towards the center is responsible for the change of momentum.

This force is that special “centripetal force” that Hazel and Ira encountered going around the curve in their car.

Note:

All non-straight motions are caused by a centripetal force.

If the trajectory is circular, it’s easy to see that the centripetal force points to the center of the imaginary circle. If the trajectory is uniformly curvy, at each point there can be many instantaneous “circles” and the forces would point towards their centers.