Contents
- A Little Bit of Galileo
- A Greek Version of Here to There
- Getting From Here to There: At Constant Speed
- Now For Something Completely Different: Feynman Diagrams
- Acceleration, Galileo Style
- The Equations of Constant Acceleration
- Acceleration, In Everyday Terms
- Special Kinds of Acceleration
- Going In the Right Direction!
- Projectiles
- The Beginning of Physics
- What to Remember from Lesson 4?
Goals of this lesson:
- I’d like you to Understand:
- How to calculate distance, time, and speed for uniform and constantly accelerated, linear motion
- That falling objects all have the same acceleration near the Earth
- How to graph simple motion parameters
- That physics models the ideal regularities of nature
- I’d like you to Appreciate:
- The algebraic narratives in the development of the formulas
- The shape of the trajectory of a projectile
- That a projectile’s motion is made of two components with different accelerations
- I’d like you to become Familiar With:
- Ideas of motion before Galileo
- Some of Galileo’s life
- Galileo’s experiments with motion
A Little Bit of Galileo
“Galileo.” What comes to mind when you hear his name? That trial? A famous experiment involving a tall building? The “father of physics”? All things you might find in a short search. But there’s much more to this complicated man, so often the subject of fables that quickly grew up around his life and his sad end.
Galileo Galilei was a loyal friend to many—a famous man in Europe—and at the same time he attracted fierce and dangerous enemies. He was an accomplished musician and literary critic and yet not above vulgar student poetry aimed at stuffy professors. He was passionately independent and yet a shameless flatterer of the wealthy and powerful. His science was novel, bold, and cutting-edge, but he couldn’t shake allegiance to perfectly circular planetary orbits. He was, and still is an enigma.
He’s a fascinating character from a fascinating time—a contemporary of Shakespeare, Elizabeth I, Francis Bacon, Johannes Kepler, Tycho de Brahe, and Rene Descartes. A cosmopolitan public figure and intellectual, yet a homebody—never straying beyond Rome, Florence, and Venice.
Galileo studied many topics in what he would have called natural philosophy, but two major scientific paths will concern us: his research and enduring conclusions about motion and astronomy. In this lesson, we’ll follow his ideas about motion and postpone his astronomy…and the famous trial…for a later lesson.
great expectations
Did you ever wonder why Galileo seems to have only one name? There’s a story about that. One of his great-great-(great?) grandfathers was the original Florentine “Galileo” - a fifteenth century medical doctor and civil leader of the family Bonaiuti. So significant was Dr Galileo in Florence that the middle-class Bonaiuti family renamed itself “Galilei.” Our Galileo Galilei’s two identical names was a subtle parental reminder that he was expected to do great things. As a proud original citizen of Florence.
Except he wasn’t an original citizen of Florence! Our Galileo was born in Pisa but always considered himself a Florentine, where he lived only after the age of 10 when his father could leave work in his wife’s Pisian family business. Vincenzo Galileo was a musician and while his family maintained its dignity, their circumstances never lived up to their legendary ancestor. Vincenzo eventually returned to Florence performing and composing full time and established young Galileo’s primary education nearby. Vincenzo’s plan was that his son would be a physician. No discussion. So off to the University of Padua he was sent.
As a Student
While a medical student, Galileo accidentally discovered an aptitude for mathematics that led him to an intense but clandestine math program with the Court Mathematician to the Grand Duke of Tuscany. After a tough negotiation at home, he eventually abandoned medicine, leaving the university a year short of his degree. By this time he was doing original mathematical research (in geometry) and had caught the attention of scholars in Pisa and Rome.
Galileo made a name for himself at the university—as shockingly disrespectful. Even at a young age, he was allergic to fools and he found the faculty overstocked in that category.1 He was also impossibly resistant to the regimented intellectual system of all European universities: in every subject, philosophy, mathematics, law, logic, rhetoric, and astronomy it was Aristotle, all the time. Particularly galling to Galileo was Aristotle’s physics and there he was in good company since Aristotle’s ideas about motion had not made sense to anyone for two centuries, but his authority was absolute. Galileo—like his father—didn’t “do” authority.
He lived at home for three years and gave private mathematics lessons in Florence and Sienna while he cultivated patrons for help in finding a university position. After some rejections, he succeeded…back at the University of Pisa as a lecturer of mathematics. Where his welcome was underwhelming.
His reputation as an original mathematician was growing when his father died. As a consequence he inherited the responsibility of a significant dowry for one married sister and responsibility to provide for the other’s. He spent the rest of his life in search of a higher salary and ways to augment his income, which as a lowly mathematician at Pisa was a quarter of that of a philosophy professor. He got his break when he was offered the position of Professor of Mathematics at the University of Padua, among the most prestigious universities in Europe and safely in the progressive Republic of Venice. It was at Padua where the Galileo magic happened.
A Greek Version of Here to There
Look around you—everything is in flux. Things fall, birds fly, you move across a room, you throw a ball, the Sun is in a different spot in the sky during the day, and the stars appear to move from east to west during the night. Why? How? Our experience shows that all events but those in the sky are individual events…all different in one way or another. Regular, reliable motions appear to be reserved for the celestial bodies.
The correct understanding of everyday motion was long in coming and by Galileo’s time, everyone thought that Aristotle had nailed it, albeit with some embarrassments. Classical works had been out of reach of Europe until Greek philosophy and science essentially fell into Europe’s lap in the form of hundreds of conflicting Arabic translations in the 1300s. But translation of Aristotle’s Physics from original Greek, to Arabic, and then to Latin did not make his ideas any less confused than they originally were.
Aristotle, revered as “The Philosopher,” invented formal logic that taught people how to evaluate arguments. But while the Philosopher’s methods were refreshing, his ideas about motion were confused at best—but nonetheless became firmly stuck in the academic and Church communities where they were protected as philosophy, not as science.
Not until the end of the 16th century did Galileo shed Aristotle and lay the groundwork for the first systematic understanding of what it means for something to move. It took three centuries! Let’s lay out the basics of The Philosopher’s mechanics so we’ll have something to throw logical darts at.
Aristotle’s Mechanics and Astronomy
For Aristotle there were three kinds of motion: two “natural” and one “unnatural.”
Natural motion near the Earth was in a straight line, either down or up relative to the center of the Universe, which he located at the center of the Earth. The speed of downward motion depended on the amount of “earthy” composition of the object, and so its weight. If there was a lot of earthiness—think a rock—the object went down. If it had the property of “lightness” (a quality that’s foreign to us) it went up—think fire. So the apparent fact that every event we observe is a little different from every other event can be ascribed to the variations in the material composition of real things.
Natural motion beyond the orbit of the Moon was to be circular with every extraterrestrial body attached to its own rotating crystalline sphere. These spheres were all nested with common centers and rotated around the Earth to account for the apparently circular orbits that we see from the Earth. They included all of the known planets, the Sun, and the Moon, and even the stars all together in the outermost shell. All three natural motions just happened…um, naturally.
Unnatural motion was different. It only happens on Earth and it required a pusher, an active force that was in physical contact with the object. Therein lay one of the most obvious flaws in his model.
Rather than one consistent set of rules, Aristotle insisted that there were different physical laws for different parts of the universe.
It’s child’s play to make fun of these ideas. And I will. But Aristotle was describing what he saw in his everyday life and trying to fit it together into his much bigger, intricately stitched-together philosophical structure. Pull at one piece of that system and the whole thing tumbles apart like a game of Jenga. So while his physics was bizarre and wrong, it stuck. It had to stick because following the genius of St Thomas Aquinas, Catholicism had hitched its wagon to the hard-to-ignore Aristotelian philosophy. But people knew for centuries that it had problems.2
Galileo uncovered the modern notion of how things move and persuasively rid the intellectual community of Aristotle’s baggage.
He began to rebel while at Pisa where he wrote an unpublished manuscript, de Motu (“On Motion”). These were immature ideas, but he was onto something. One of his conclusions was right on: all objects fall at the same rate, contrary to Aristotle’s insistence that heavier objects fell faster. His data? Not the Leaning Tower of Pisa. That’s a myth. He too looked around him. And saw things differently.
Getting From Here to There: At Constant Speed
Motion is both easiest and the hardest concept in physics and so much of what comes for us will constantly stretch at ideas about what motion is and how we can describe it. So we need to start at the beginning.
You’ve been dropping things since you were a toddler and you learned the hard way that if you drop something from a high place it will more likely break than from a low height. You learned that the harder you throw a ball, the faster it will leave your hand, the more damage it can do to a window, and the farther it will go before landing—and that it always comes down.
Since you started driving, you began to develop an intuition for magnitudes of speeds and you do speed-arithmetic all the time: if you travel at 50 mph for 2 hours, you will have gone how far? 100 miles, right?
In fact, you know a lot about speed and I wouldn’t shock you if I wrote a sentence-equation that defines it.
Here it is. Admire it because it’s going to evolve:
Simple! But.
From our QS&BB perspective, there’s a lot to unpack about this simple mathematical sentence and it will all matter as we move ahead. Just a taste:
- What are the units of speed? If the sign says “Speed Limit, 55,”
 how fast is that? mph? meters per second? km per hour? stadions (look it up) per fortnight? It would be silly to just say “55” wouldn’t it. Wait. That’s exactly what our speed limit signs say. So you even intuit speed units.
how fast is that? mph? meters per second? km per hour? stadions (look it up) per fortnight? It would be silly to just say “55” wouldn’t it. Wait. That’s exactly what our speed limit signs say. So you even intuit speed units. - If time doesn’t march on, we’ve not moved. But what is time? “ Tubby…paused. ‘Time,’ he added slowly – ‘time is what keeps everything from happening at once…” 3 We’ll see time take on a new meaning.
- The final frontier, Space, is either “just there” or it’s a relationship among extended objects. If all of the things in the universe disappeared, is there space left over? That’s an old, contentious issue and maybe was finally solved by Einstein.
- What’s the difference between space and time? In “speed” they are just two sides of the same coin, or two sides of the same ratio. But don’t you usually think of them as different things? One’s not more important than the other is it? Eventually, we’ll let Einstein chime in here.
- Particular speeds seem to be important. Mr Galileo taught us about one and James Clerk Maxwell and Albert Einstein taught us about another. (There he is again.)
From that simple word-equation, so sensible and so obvious, I’ve hinted at at least five complications. We have learned to ask simple questions and discover that they sometimes lead to important and surprising directions.
motion: it’s everywhere
Almost everything in physics boils down to: motion. (Even boiling.)
Whether it’s runners on a track, the cosmic rays piercing us all the time, orbiting planets, electrons in a wire, electromagnetic waves, quark wavefunctions inside a proton, electrons and holes in a semiconductor, or the stretching of spacetime itself. Everything is about “motion.”
These first lessons on the physics of my grandparents’ generation will establish the language and tools that we’ll need in order to pursue the more exotic forms of motion and we’ll become skilled at manipulating concepts (and their attendant symbols) like velocity, kinetic energy, mass, momentum, and force. Each of these terms has a sixteenth to nineteenth century origin, but each has managed to keep up with the times as layer upon layer of subtlety is discovered about each of them as we dig deeper and discover more.
But at its most basic, our physics will be all about how to get from here to there and from then to now, and to be able to explain how that happened and predict what will come next.
Speed in Modern Terms
To us, motion and its measure—speed—is a simple matter. Our cars and even devices on our wrists readily tell us how far we go, how long it takes us to get there, and the rate at which we do it. We can be penalized for traveling at rates that are…too enthusiastic. Speed, or its more sophisticated word-cousin, velocity, is so familiar to us that we hardly pay any attention to just how fundamental it is. Let’s start this very slowly (no pun intended) since some of our more sophisticated physics later will build on a strong underpinning of a few basic concepts. Speed is one such concept because it’s a blend of two even more fundamental concepts of space and time.
Speed is a rate. For example, 60 mph describes the change in our spatial position and how long it took to make that change. Like all rates, it’s a ratio with respect to time and we’ve already agreed:
Words are clumsy when we’re trying to be precise. Let’s make this more compact by inserting customary symbols to get rid of the English words. Here are some grammar rules in QS&BB:
-
We’ll limit ourselves almost exclusively to motion in one dimension in space.
-
We’ll use the symbol $v$ for speed (because customarily, we’ll speak of “velocity”…more about this below).
-
We’ll use the symbol $x$ for distance in one dimension, regardless of which direction it points.
-
We’ll use the symbol $t$ for time and almost always presume that we set our clocks so that the beginning time of any interval is $t_0=0$.
-
Oh, and we’ll use the subscript $\text{ }_{0}$ to indicate the beginning of some time or location interval–” $t_0$” or “ $x_0$ ”– in a sequence of events.
-
We’ll use the Greek symbol Delta, $\Delta$ to mean “change of”…this will come up a lot.
So our formula for calculating speed changes from the English sentence in Eq. \eqref{speedwords} to a mathematical statement:
Is this simple thing worth the a whole paragraph of lead-in? It’s actually surprisingly subtle, this simple highway-sign equation, and we’re going to revisit it over and over again.
Calculating a Speed
Some traditional jargon and nomenclature to make your…okay, my life easier. “Change” and “change-of” always means the difference between where you are as compared with where you were. Suppose I start out with $\$100$ and my wife gives me $\$50$. What’s the net change in my net worth? We can represent this simple transaction as
which is the definition of our $\Delta$ : always “the end minus the beginning,” the final value of some quantity minus the initial value of that quantity.
Remember that we’re using our standard notation in which the “initial state” of any quantity will be decorated with a little “0” subscript, like $x_0$ here. The “final state” will usually have no subscript and just be $x$. So $\Delta x = x-x_0$ and $\Delta t=t - t_0$. Get it?4
sing along
Remember the rule. When you see the 🖋 and a colored background, you should open your Notebook and copy what comes next until the background returns to white. It’s the path to your brain.
The story of speed
🖥️ Please answer a question:
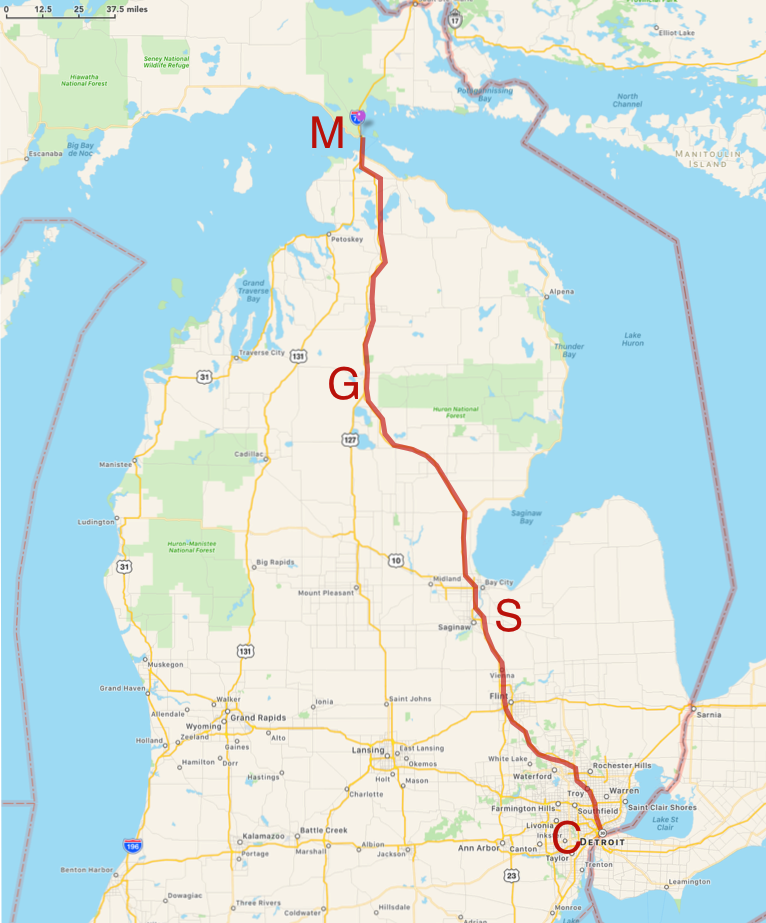
Wait. Nobody does this.
Glad you asked. You mean I’m the only one?
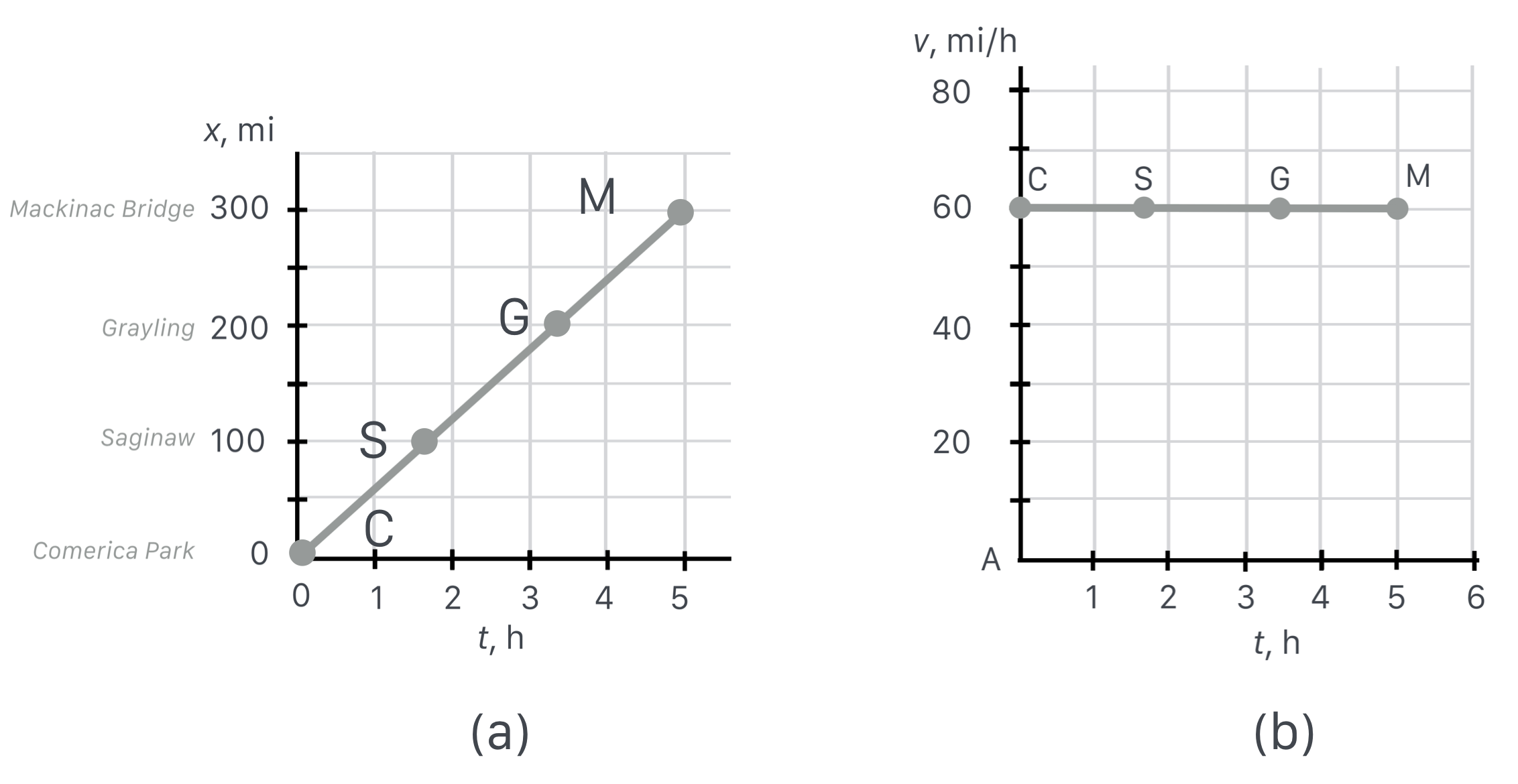
That straight line in the distance plot in (a) is a familiar thing. Let’s make a model of the motion and take our definition of speed and manipulate it a little to support that calculation that your brain did before. Notice that all we used in our mental calculation was the beginning (C) and end (M), without regard to what happened in-between. That’s the very definition of an average and we’ll use the notation $\langle Q \rangle$ to represent the average of a quantity $Q$. From the definition of speed:
You’ve just created a model for motion. In fact, you’ve also done some geometry since:
is the equation for a straight line. Do you remember some time in your past algebraic life saying, “y equals m x plus b” …$y=mx + b$? Here, “$y$” is our distance, $x$; (confusingly) $x$ is our time difference, $t$; and $b$ (the slope in the equation) is our average velocity, $\langle v \rangle$.
So we can see that the straight line from our plots has a slope that’s equivalent to our average speed. Now I don’t know about you, but I can’t drive precisely at 60 mph for 10 minutes, let alone for 5 hours. So here’s a more realistic image of what the distance versus time relation might be.
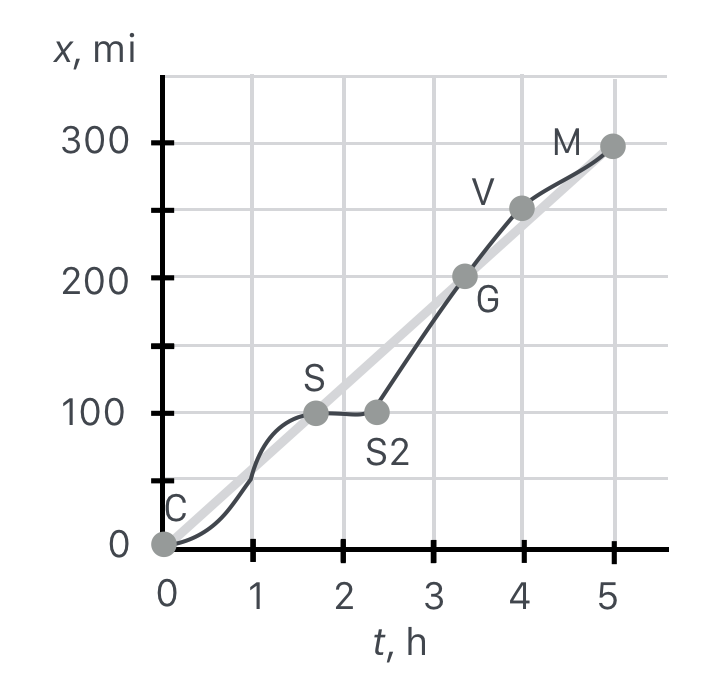
Here the dark line is meant to represent a more realistic journey with the light gray line showing the originally ideal, constant velocity trip. Notice that we start slow and speed up and then at Saginaw we stop for dinner: the distance is unchanged for almost an hour until point S2 when we start up again. And boy, do we ever. We fly through Grayling G) on to Vanderbilt (V) and then more slowly, get to the bridge.
Let’s analyze this while feeling sorry for ourselves about that speeding ticket.
🖥️ Please answer a question:
Can you see that the average speed is the same for the realistic trajectory and the originally idealistic steady-on-the-gas picture? All the average depends on is the beginning and the end.
explanation
If you want to know more details, then you’d need shorter time intervals. In each successively smaller interval you’d know the speed more precisely and in the limit where you’re just at a point on some curve of distance – well, that’s the instantaneous speed. That too is an idealistic notion since any measurement of speed would require a finite time interval. Of course your speedometer is calculating an average also, but the time interval is so short that we tend to think of the reading in the cockpit as our speed right now.
Multiplication and Geometry
Here is a neat way of thinking about algebra that will give us insight into many different circumstances. We’ll use it a lot. Let’s simplify our model to be just $x = vt$. Do you notice anything familiar about the form of that equation? Maybe this will remind you.
Suppose my yard is chalked with foot-long markers. (You mean yours isn’t?)
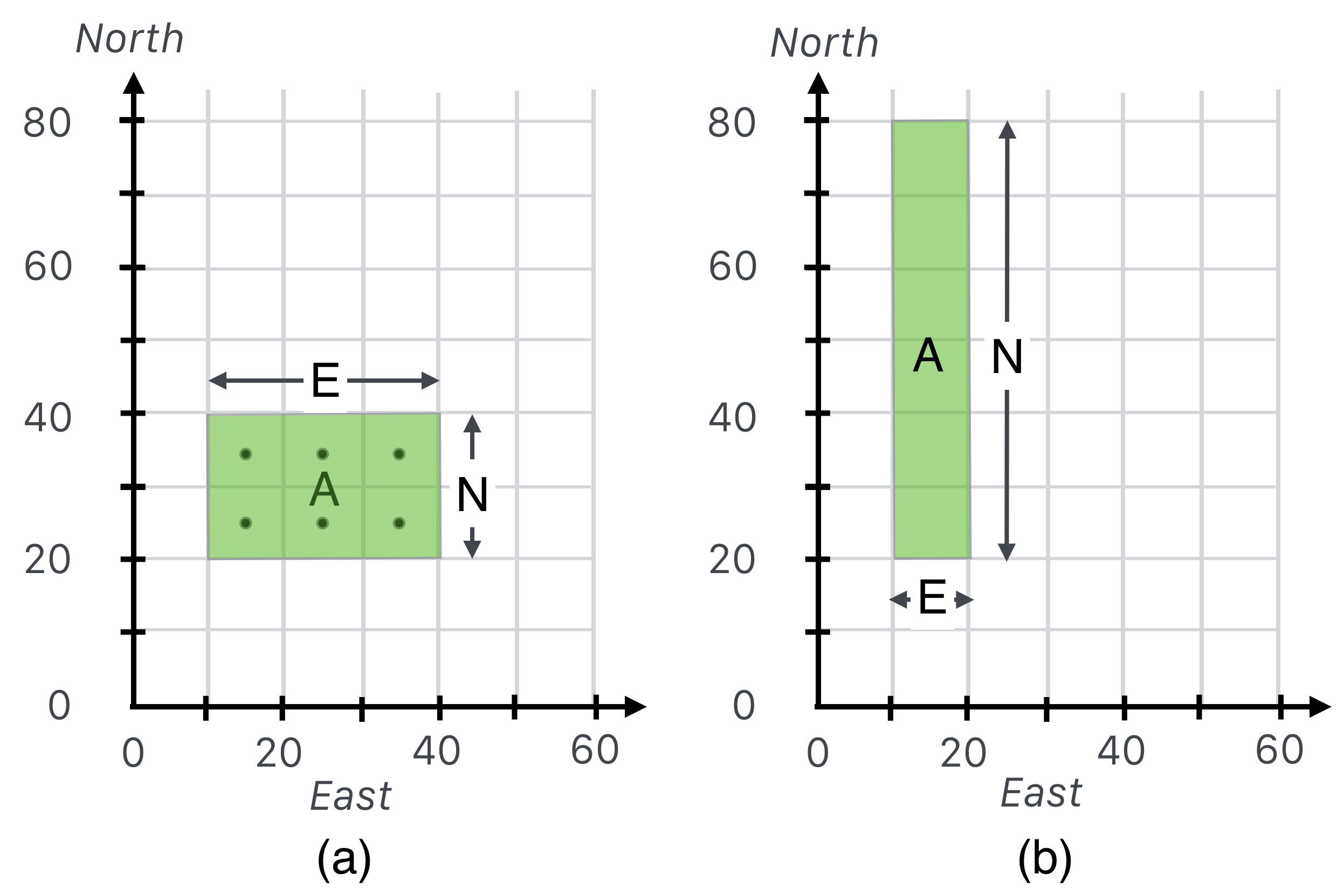
What is the area of my yard? You’d quickly calculate for (a) that it’s $20 \times 30 = 600$ square feet, right? That is, you remember that in order to calculate an area you multiply the width times the height:
Suppose now I want to sell an eastern parcel to a neighbor leaving me with only 10 feet of width. But I want the area of my yard to remain the same. That can happen if I can buy land from my northern neighbor. How much do I need to buy? What must the north - south dimension of my yard be in order to keep the area of 600 sqft? The yard drawing in (b) answers that question. We simply modify the area formula
making one variable on the right small and the other one large in order to keep the total area the same. Of course you could calculate the area in many ways: cut out the picture and reform it into a different rectangle. Or notice that there are dots in the squares of (a)… count them up and you’ll find there are six. So the new yard areas also has to have six dots-worth of yard-squares. (Each rectangle is worth 10 sqft as you can see.) We’ll make use of this simple idea over and over.
Like now:
Notice that $x = vt$ is actually the equation of a rectangle which we can represent as areas in velocity and time. We 300 miles at a steady 60 mph and it took five hours. We can make a geometrical model of this motion as in (a) below:
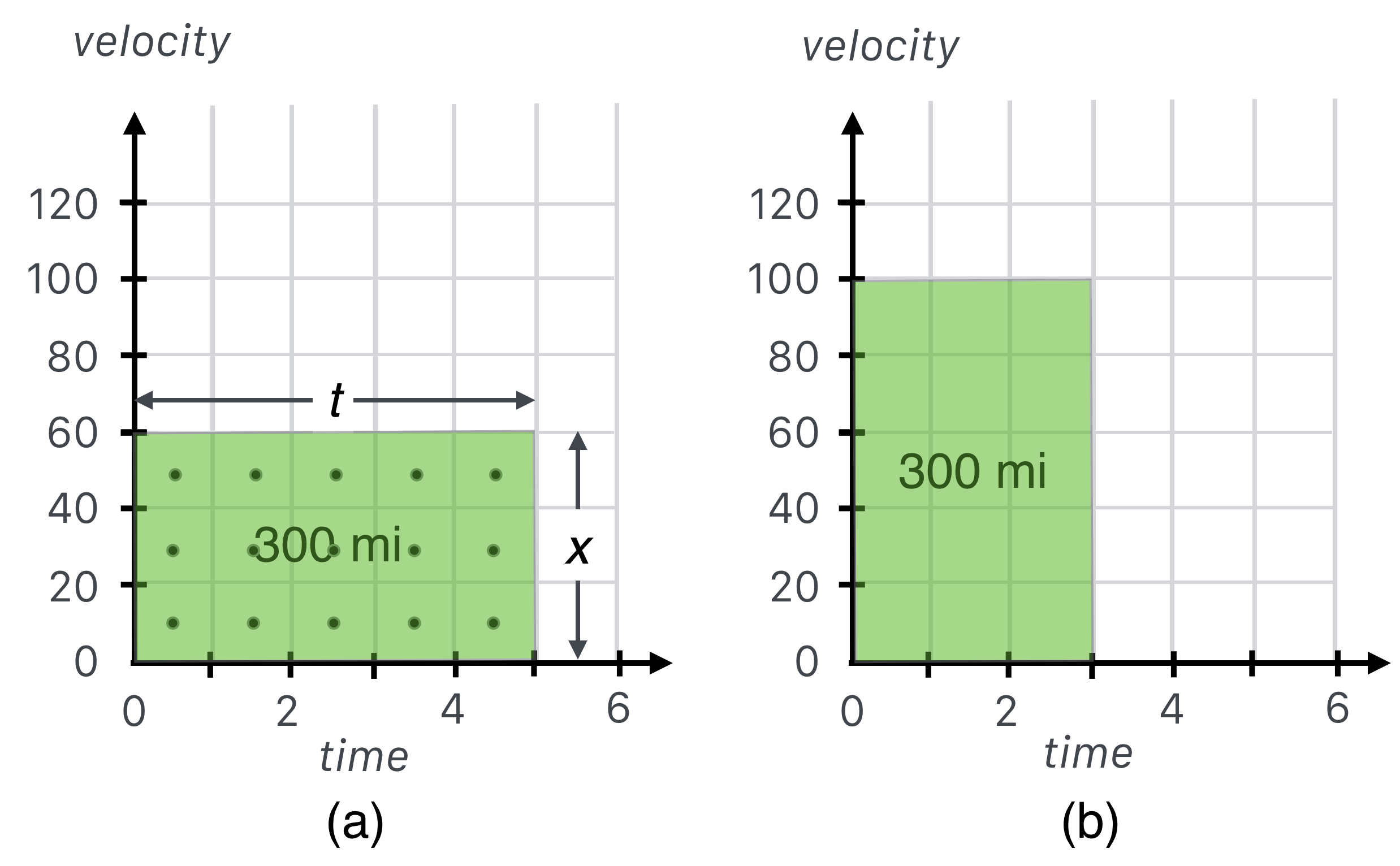
I don’t advise it. But you get my meaning.
We’ll be able to do this many times for many different circumstances. Yard acreage or even speeds seem obvious, but we’ll encounter more complicated ideas for which this geometrical thinking will actually lead to physics-insight. Trust me, I’m a doctor.
🖥️ Please answer a question:
algebra and geometry
I’m impressed by this sort of thing. Look what we did. We took our intuitive notion of a constant speed in an English paragraph, turned it into a simple algebraic equation, and then turned that into a graph that will give our location at any point along the way. And then we insight into the physics by thinking of our speed equation like an area equation. This happens often—some algebra leads to a geometrical relation. In physics we tend to treat the plot on par with the equation as an “explanation.”
The problem with this story is: how did we magically get to 60 mph? We accelerated and therein is another Galileo story and a fable.
Now For Something Completely Different: Feynman Diagrams
Richard Feynman was an unusual man. We’ll rely on him periodically as he explains some tough concepts in often bumper-sticker-sized insights. One of the things he did was create a language for dealing with the bizarre concepts of relativistic quantum field theory (a mouthful, but you’ll form those words yourself later) and how we use it to describe the interactions of elementary particles. His language is a sophisticated brand of mathematics, but it comes with a highly visual diagramatic tool that we can use all by itself. It’s already inherent in the graphs we just drew for distance as a function of time for constant speeds. We call that space, Spacetime and Feynman Diagrams are Spacetime Diagrams. Let’s think differently from how you may have before.
Space Diagrams and Spacetime Diagrams
Ultimately we’ll want to appreciate the collisions of elementary particles and the best image I can think of is a pool table with smooth balls moving around on its surface. Let’s do that. I’ll repeatedly refer to two kinds of geometrical spaces:
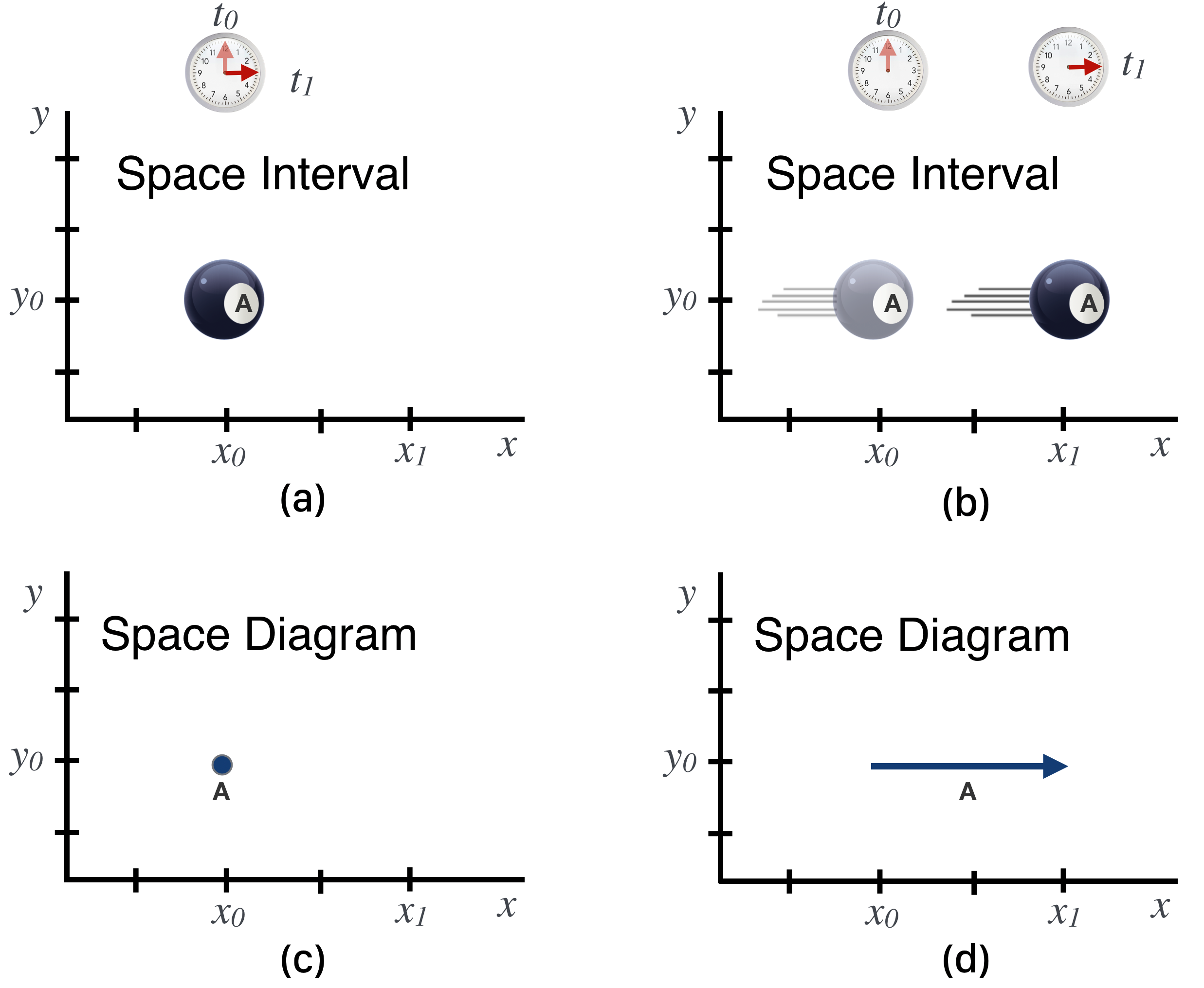
- Space Diagram. A Space Diagram will be a drawing that a moving object might take in space, for us, $x$ and $y$. Sounds simple. If you were to draw the path you took on a road trip you would mark a line on a map with a pencil, following the roads, right? But implicit in this line is that the time that elapsed in your journey is implied, but not explicit. At every mile-marker on the highway you could have marked down the time and it would be more evident. A curve in a Space Diagram is a trajectory in space coordinates where time is kind of in the background.
- Spacetime Diagram. A Spacetime Diagram is one in which time is now explicit as one of the coordinates. Since paper is two dimensionally flat for us that means we have to imply one of the formerly evident space dimensions and call out only one of the two (two of the three if we were in three-dimensional space). The result is a Spacetime geometry which only became a thing…with the other guy whom we’ll be constantly referring to, Albert Einstein. Spacetime is a thing…in his Special Theory of Relativity. A trajectory in Spacetime is a curve drawn at a particular place at a particular time.
A buzzword: “Event.” An **event** is a physical happening at a single point in space and at a single time. If you have a ruler and a clock…you can fully characterize an event. . Touch your screen right here: $\rightarrow$ x $\leftarrow$ and look at your watch. The coordinates of the “x” spot and the time that you touched it define that physical act completely.
Another buzzword: “interval.” We'll refer to the space and/or time differences between two events as an **interval**.5
Some close-reading here:
This figure shows these two simple interludes [notice the clocks at the top registering the initial time (transparent arrow) and the final time (solid arrow)] as we'd watch them unfold on the table's surface: at the top (a) the ball is just sitting still and top (b) its moving to the right. In (c) and (d) we see the abstracted Space Diagrams (not pictures of balls, but dots) for each interlude.
The important thing to note is the times. Above each event there's a clock and two times that have elapsed. In (b), the moving interlude, it's obvious that the time value at position $(x_0, y_0)$ is $t_0$ and the time when the ball has traveled to position $(x_1,y_0)$ is $t_1$. In (a) it's simpler, but sort of an different way of thinking. The ball is stationary but time…as they say…marches on. I've represented that on the same clock face at the top.
The Space Diagram for event (d) is just exactly that line you'd draw on a map to trace out your journey. The start and the finish points are "events" for us and the space traveled and the time elapsed are "intervals" for us.
This next figure shows a different way of representing these two events.
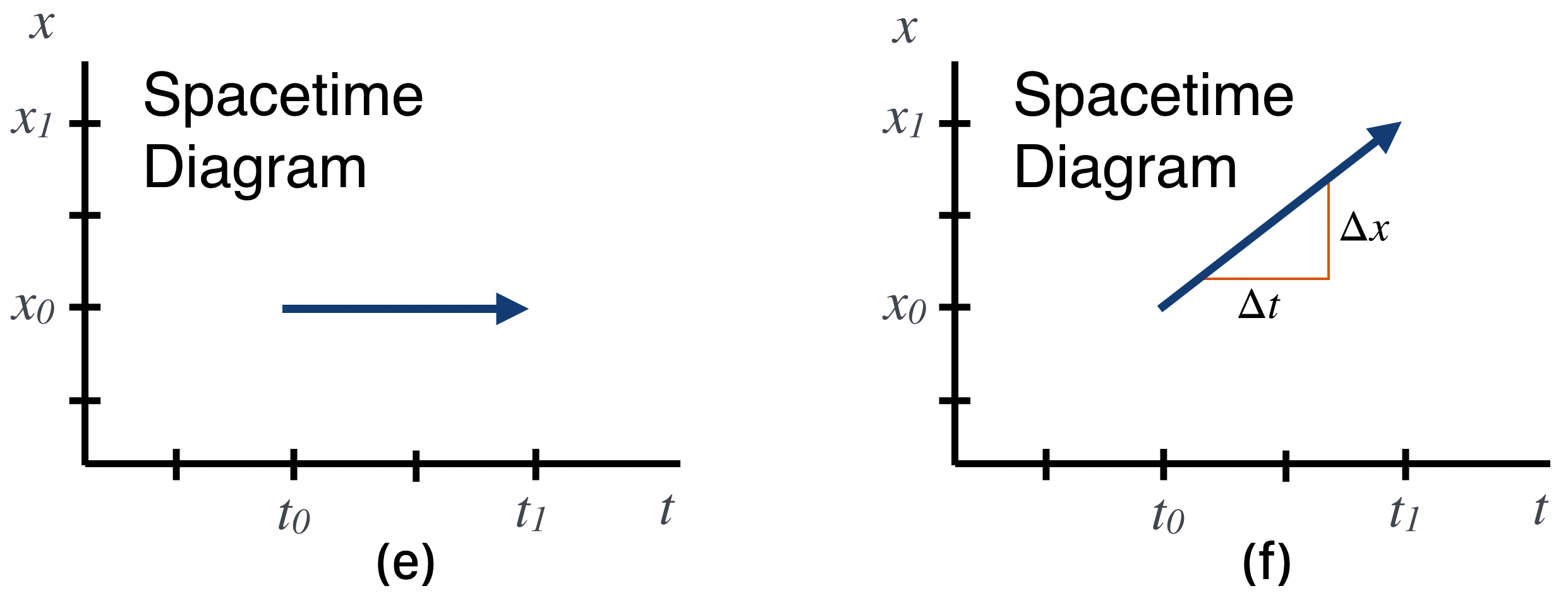
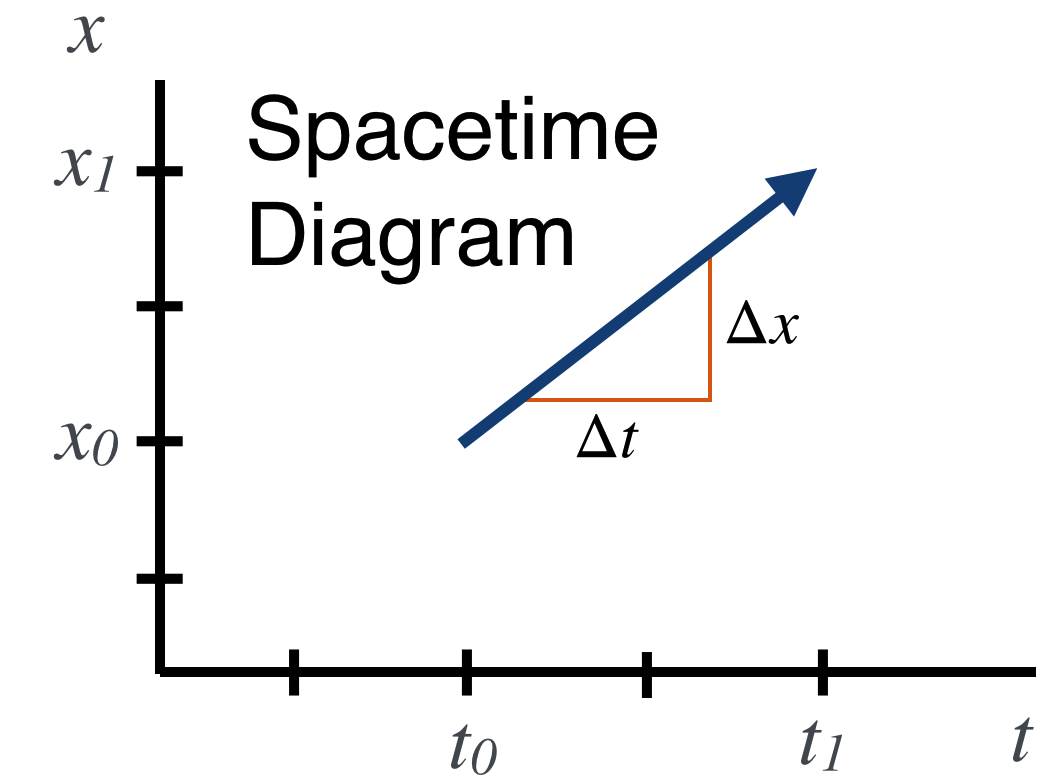
We’re going to love Spacetime diagrams!
We’ll come back to this when we think about colliding things together, when we talk about Relativity, and then again when we talk about actual elementary particle physics collisions in our labs and in the early universe.
Acceleration, Galileo Style
Very early on Galileo recognized that the unnatural/natural motion notions of Aristotle were wrong. For example, Aristotle insisted that if dropped, two objects made of the same material but of different weights would not hit the ground at the same time. The heavier one would be more “eager” to go to its natural place (the earth’s center) than the light one. He explicitly linked an object’s weight with the speed at which it would fall. Aristotle didn’t do “quantitative” so his notion of “faster” was a proportional statement.
It was clear to everyone that the further an object fell, the longer were the differences between roughly equal times. All one had to do was watch water drips from a roof…the distances that they travel in a given time are much longer near the ground than when they first leave the edge. Longer distances traveled in equal times means velocities increase in equal times…that’s acceleration. As I said, everyone knew that. But in what manner does this change in speed happen: some said, as a function of the distance while others said as a function of the time. Inquiring minds wanted to know! And many tried.
Galileo first started to think differently about motion when he was a professor at Pisa. That’s where he was supposed to have dropped a wooden and iron ball from the Leaning Tower, although we know that he couldn’t have done it the way he described it. His first, unpublished pamphlet on motion was a mixture of an old language and his attempts at a new one, and so was not quite there yet.
His conclusions about falling objects were heavily influenced by his fascination with the pendulum. Let’s leave that until after we work out what he found by experiment.
Pisa To Padua
Galileo’s salary as a mathematics and astronomy professor was abysmally low and he was clearly ready for a more lucrative position—plus nobody in Pisa was eager to have him around. So after three years, when he was offered a job at the University of Padua at the age of 28 he took it and stayed for 18 years until 1610. Not only was his salary higher, the Venetian Republic was a much more independent region of Italy.6 Indeed, unlike Florence in Tuscany where connections to Rome and the Papacy were long-standing, Venice was often in the Papal Doghouse for its independent ways (five popes essentially excommunicated the entire city…and five popes changed their minds). Here Galileo became a popular professor, he created tools for military use that he was able to sell, including a manual. He settled into a common-law relationship with Marina di Andrea Gamba with whom he had three children. But money continued to be problematic and so he and Marina took in students for tutoring and rental income into their crowded home.
While Galileo was in Padua, he began his experiments with moving objects. His original Padua ideas were unformed but he reworked them as he further shed his Aristotelian influences. He had a workshop at his home and eventually hired a toolmaker.
He determined to get to the bottom of falling (hee hee) and he wasn’t the first. Some linked the speed of a falling object with its density. Others, like Leonardo da Vinci speculated from some fanciful geometry that an object would fall a particular distance in relation to the time interval. The figure below shows this. The left shows the distance that an object would fall in successive, equal time intervals as da Vinci imagined it. In the first unit of time—think, say a second, the object would fall 1 unit of distance. In the second unit of time, it would then fall 2 units of distance, in the third, three…and so on. That’s indeed an accelerating object, but it’s not a constant acceleration.
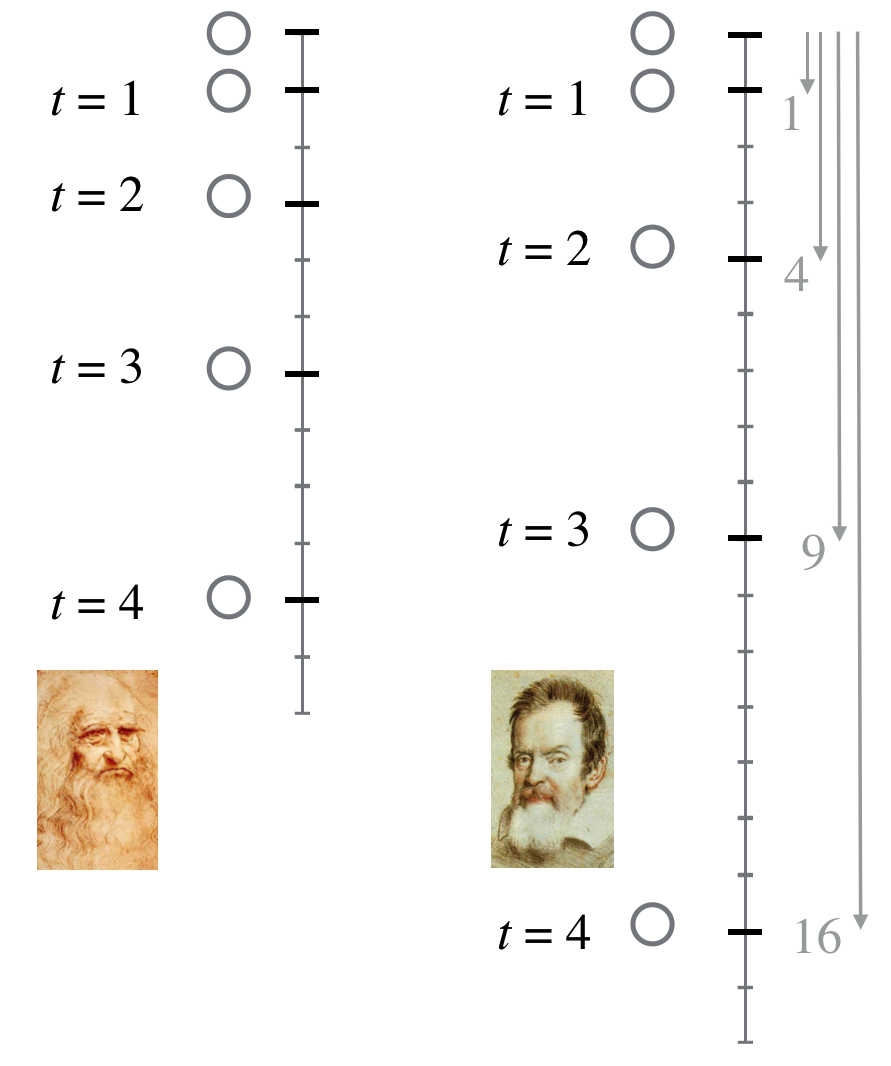
There was another suggestion that came from a geometrical analysis in the 1300s: if the acceleration in free-fall were constant, then in each successive unit of time the distance of an object would increase according to the odd integers!
So, in time intervals 1, 2, 3 seconds, the distance fallen would have values 1, 3, 5 units. This is shown on the right side of the figure. Look at the lines drawn in on the right of this figure. Notice that the first interval of time leads to 1 unit of fallen distance. The second interval is 3 units (remember, the odd integers), the fourth…of course, 5 units. Now add them up for the total distance fallen as time increases: the first unit of time, 1. The second unit of time $1+3=4$. The third unit of time, $1+3+5=9$, and so on. 1, 4, 9… are the perfect squares of the time intervals, 1, 2, 3… Seeing falling objects that increased their total distance by the perfect squares would be the smoking gun for evidence of a constant acceleration.
Why didn’t someone just measure it two centuries before? First, the idea of an experiment had just not caught on very much. One thought about things, consulted Aristotle, and argued. Not much tinkering.
But also things fall fast! Even in the early seventeenth century precision time-keeping really didn’t exist. Galileo was near Venice, home of one of the oldest and most celebrated striking-clocks in history, but to measure times as fast as those of a falling body? Not possible. But this guy was clever.
What Did He Do?
Galileo tricked nature in 1604 he found a way to dilute gravity so that he could make timing measurements using contemporary tools. Instead of dropping a ball, he let it roll down a gentle incline. He reasoned that whatever pull a ball felt in free-fall would still govern the reduced acceleration in a slow descent down an incline: inclines of only two or three degrees were ideal. The figure below shows his setup and his results.
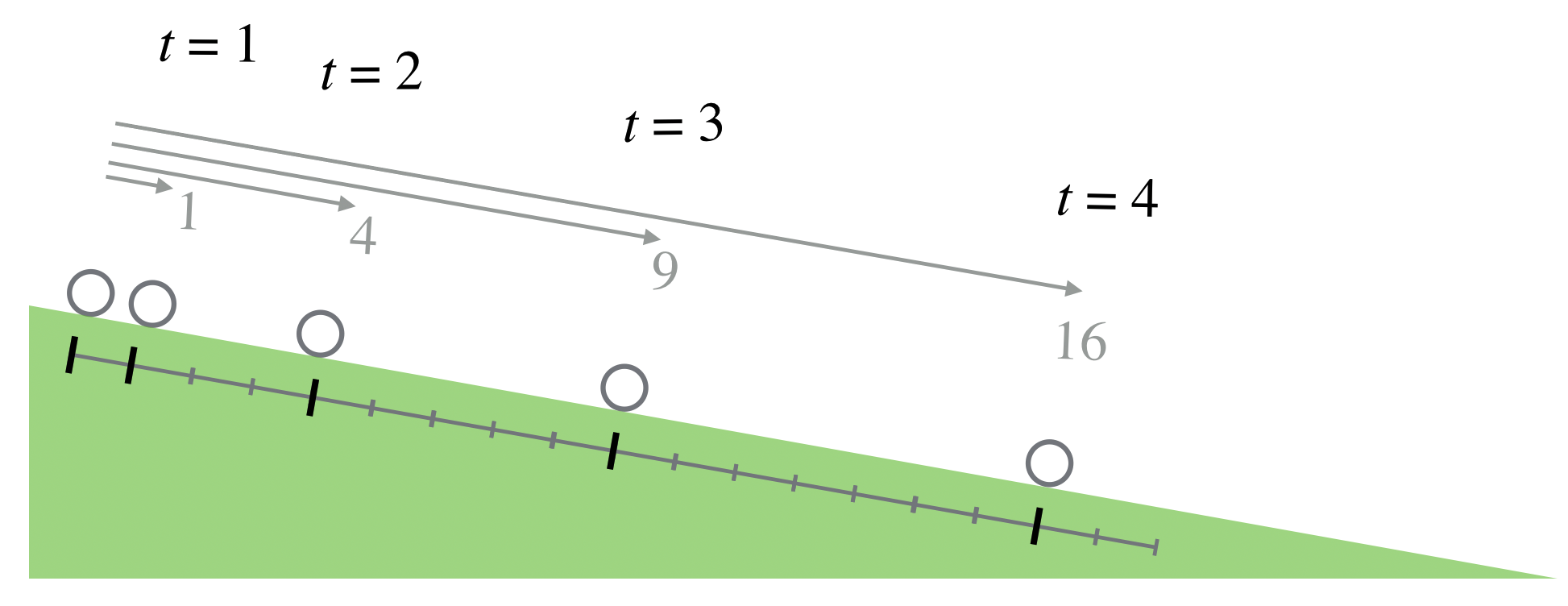
Galileo was good with his hands, and appreciating that he needed to reduce the effects of friction and other extra impediments to determining the real rules, he built inclines with finely machined grooves to minimize the effects of friction and then made elaborate schemes to measure the time that it took for an object to “fall” as it rolled slowly down. He needed a clock, so he used his pulse. When that wasn’t sufficiently regular, he hired a string quartet to play at an even meter. He eventually invented a “water clock” that slowly dripped at a regular rate and it was with that, that he was able to see how far a ball would roll during each “tick” of his water clock.
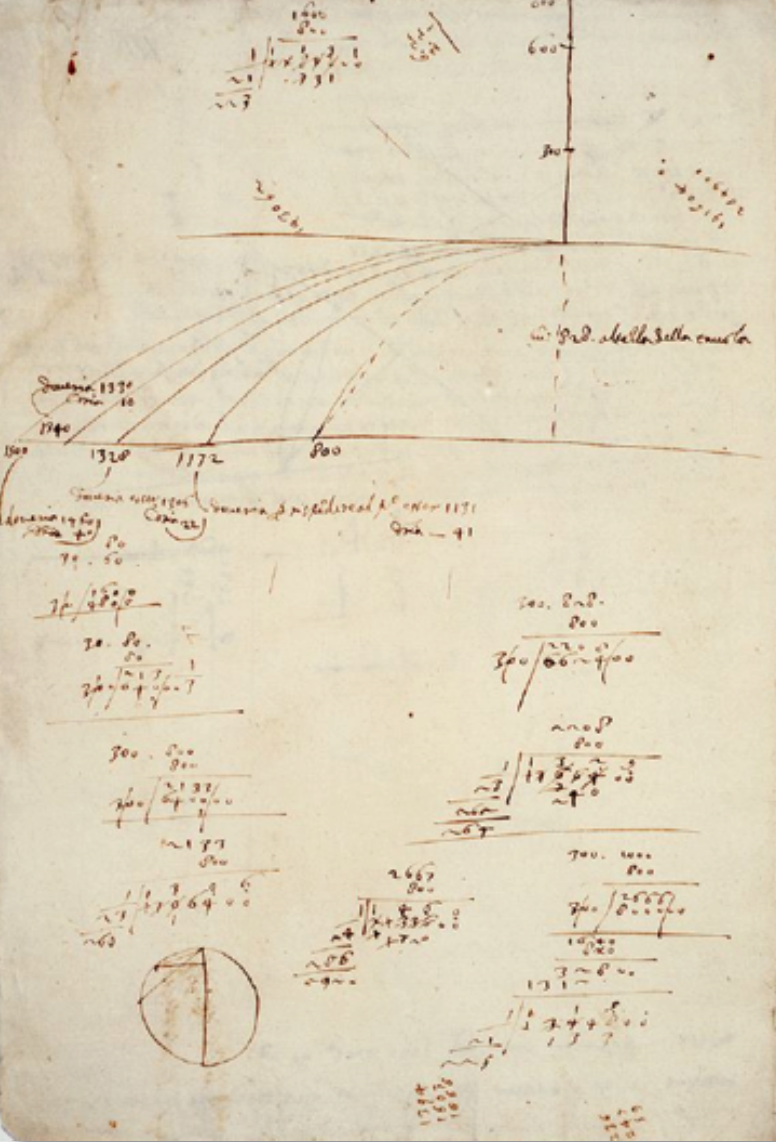
How do we know that this was a real measurement and not some thought-experiment? Because he told us. Galileo kept careful records of his experiments and these have been preserved.
This amazing figure

shows the aha! moment in one of his pages where he’s taking his measurements, scribbling around the sheet, and keeping his records in the upper left hand corner. The preeminent Galileo scholar, the late Stillman Drake from the University of Minnesota studied these notebooks and found something intriguing. Notice that the numbers 1 through 8 are clearly visible in the middle column in the inset. The numbers on the right are the distances he measured down the plane, and are a result of some of the arithmetic on the sheet. But the numbers in the left-hand column? Drake noticed on this particular page that the ink used in the left column was different from the ink in the actual data-taking on that page. In fact that ink was consistent with pages that came from entries many days later. Look carefully at those numbers…they are 1, 4, 9, 16, 25, 36, 49, 64.
a most important moment
The presumption is that Galileo took the data, pondered the results, and then later realized that his measurements fit the time-squared rule and came back later to the page to add them in. Imagine what his emotional state must have been when he realized what he’d done! He’s demonstrated that the acceleration of a falling body is constant. I think this is one of the most important documents in the history of science.
Little $g$
Let’s do what we almost always do when confronted with data: plot it. I can just make out the numbers in his manuscript. The units for both time and distance are a little unusual, so we’ll leave them without dimensions.
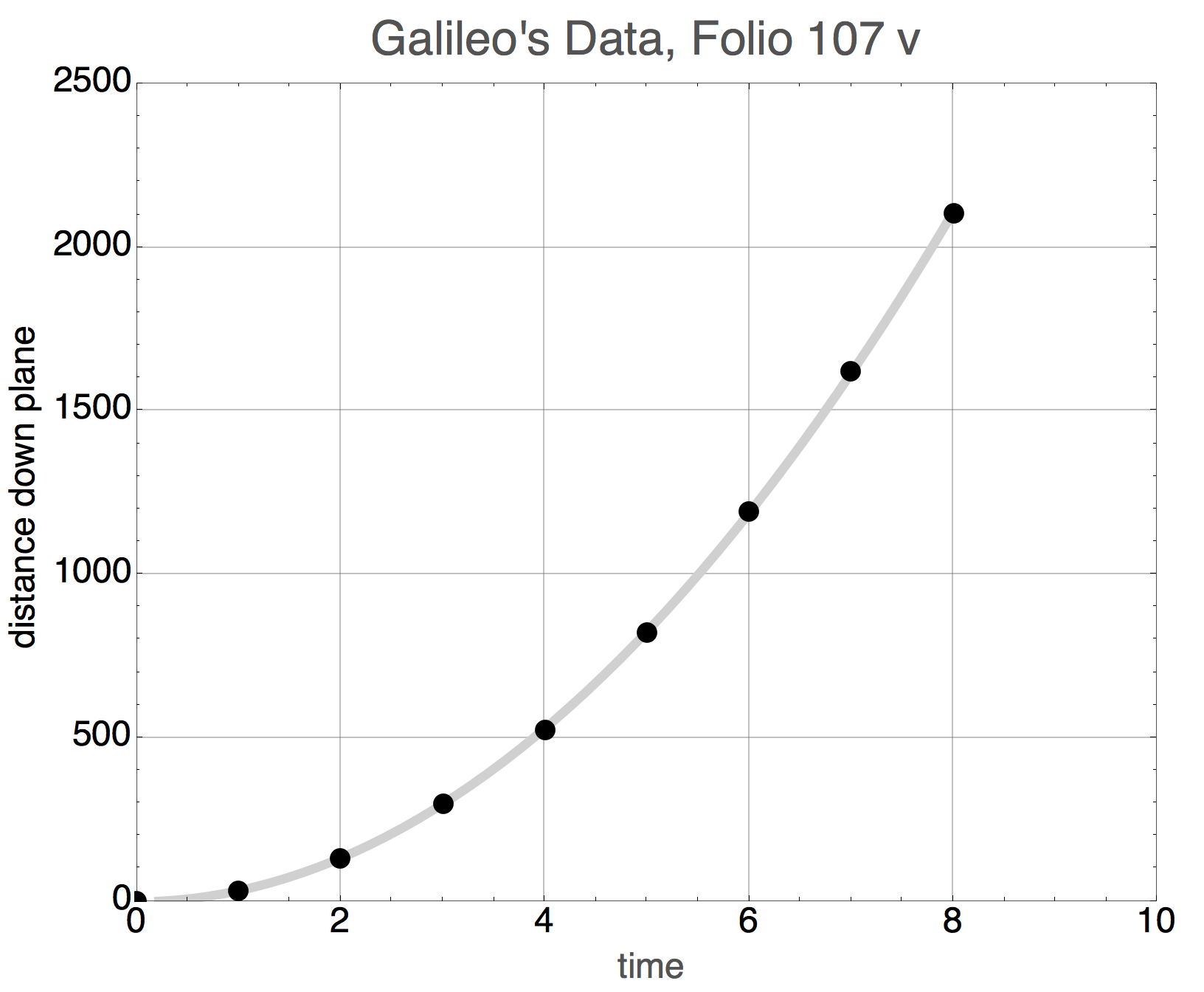
This is a familiar shape and the squares in the data above give us the clue that this is the shape of a parabola, and it’s a pretty good one. The curve is not drawn through the points, but rather is a fit to the functional form of a parabola. So we could write the equation of this curve as
The constant comes from measurement and in modern units we write:
where we give this special, constant acceleration a name, the “acceleration of gravity,” $g$, or “little g” which is roughly 32 ft/sec/sec, or 9.8 m/s$^2$. This was first measured by Isaac Newton a generation later using very long pendulums.
little g
Objects near the earth’s surface fall with essentially constant acceleration of $g=9.8$ m/s$^2$.
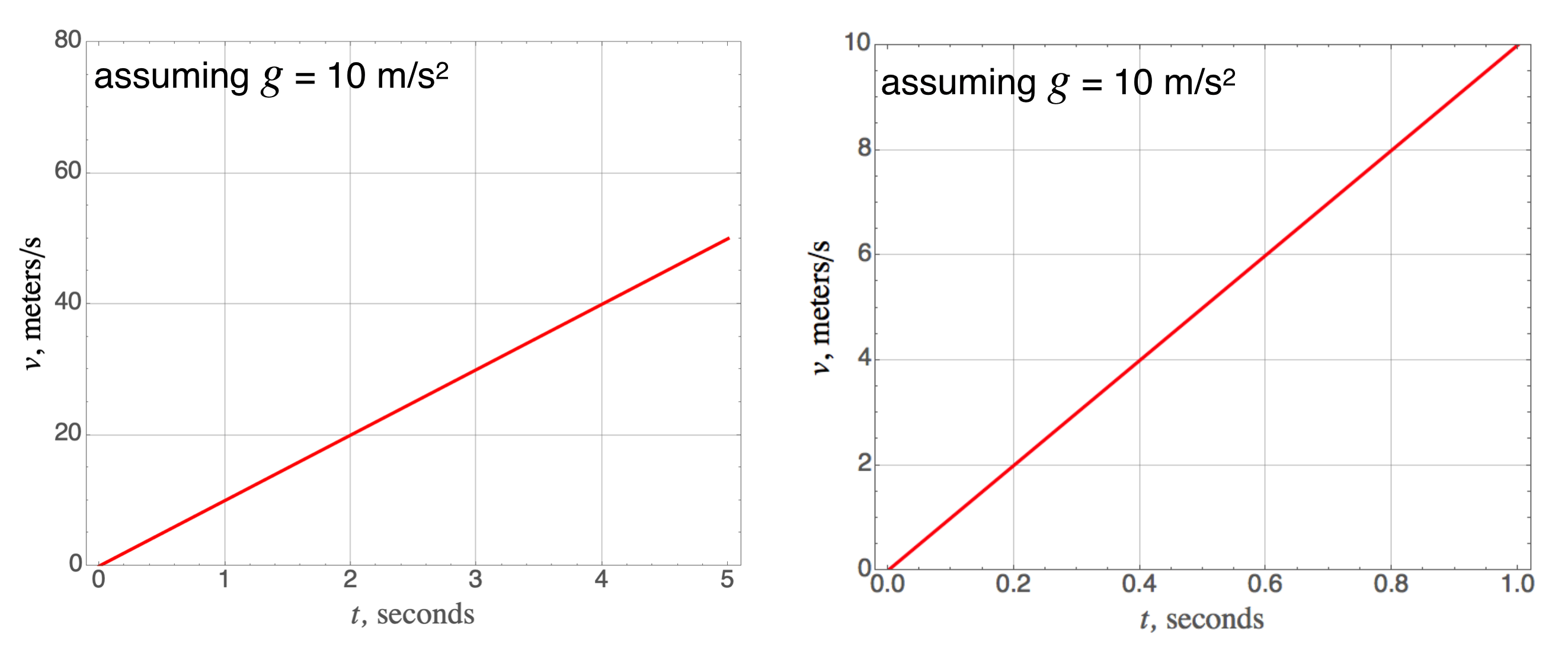
We can summarize his results in a series of plots which represent this model of falling objects. Little $g$’s value of 9.8 m/s$^2$ is so close to 10 m/s$^2$, that we can often get away with that rounded value. The following plots do just that.
First, the velocity changes linearly with time if the acceleration is constant – here, that lazy 10 m/s$^2$ .
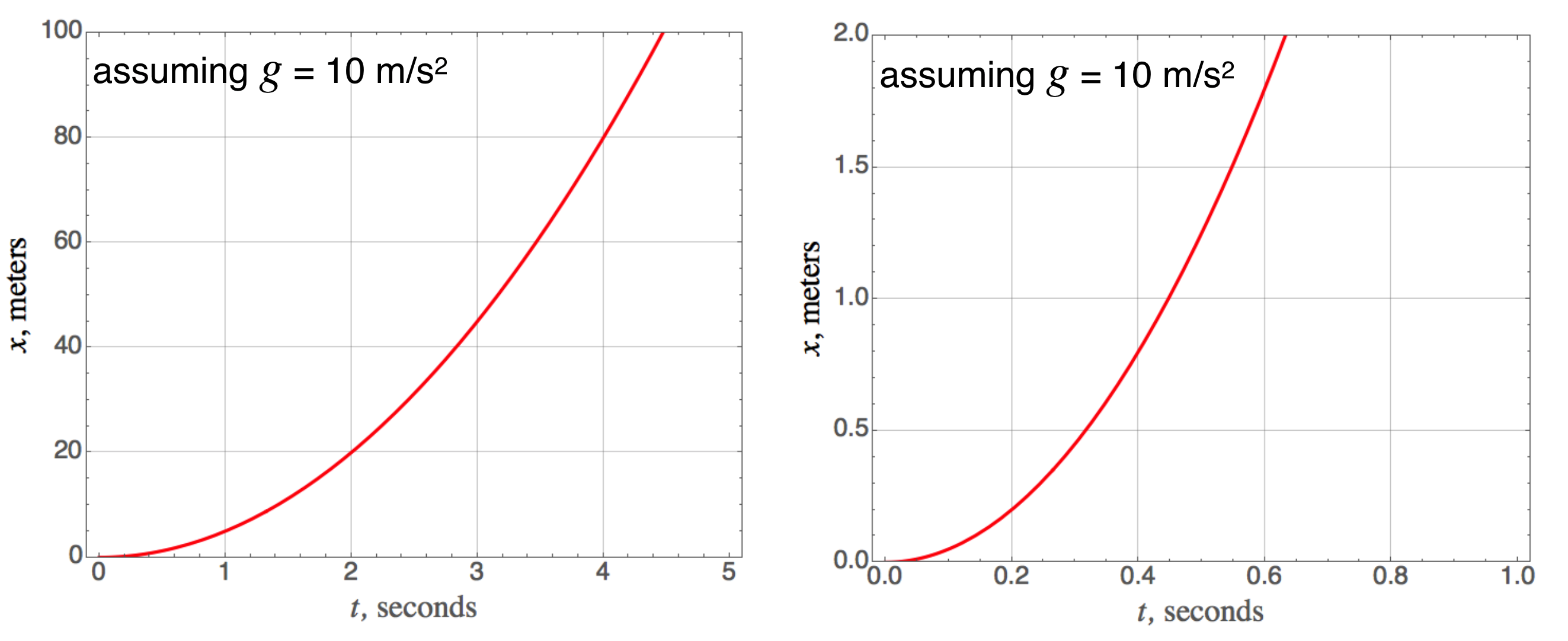
Here is the quadratic distance-time relationship stemming from that constant acceleration:
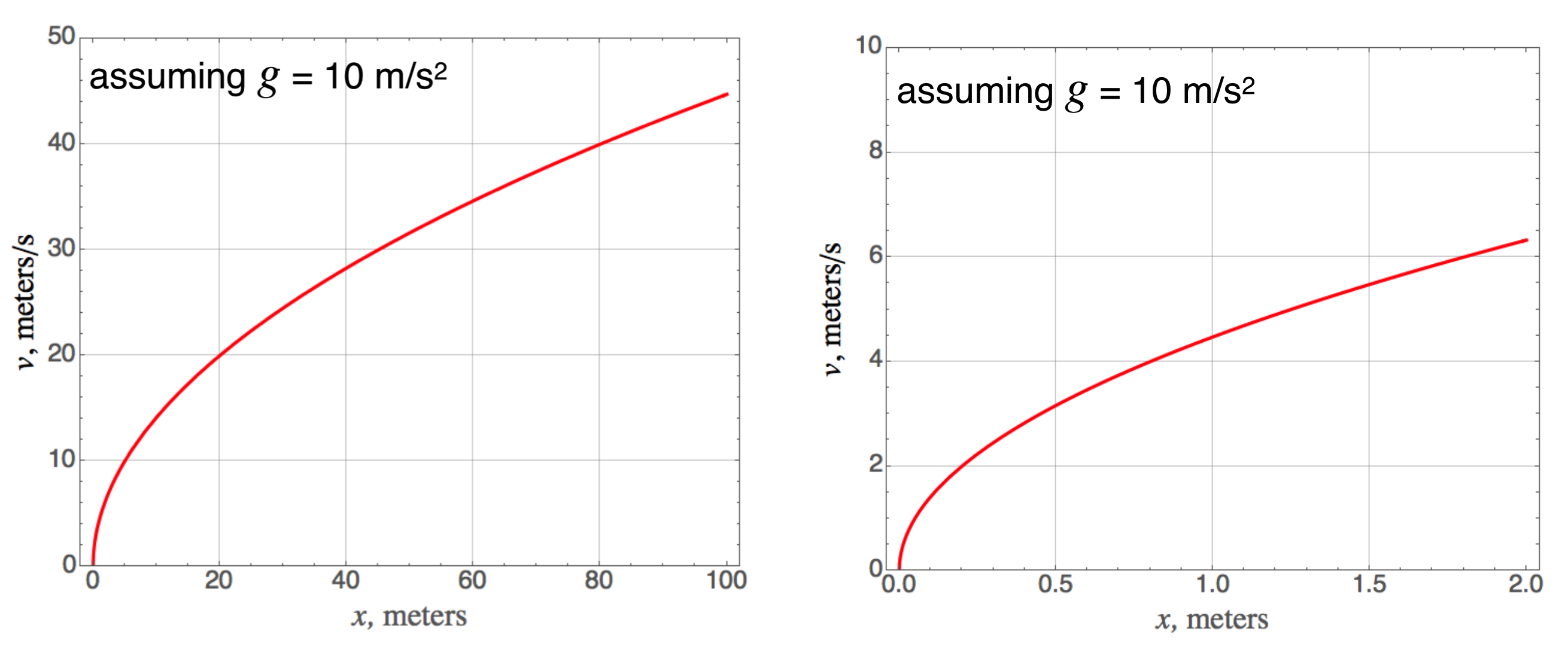
We could combine the equations for constant acceleration and eliminate the time coordinate to get a relationship between the speed and the distance fallen. Here is that:
🖥️ Please answer a question:
This is not the complete story…see the section below about air resistance.
The Equations of Constant Acceleration
Some of the graphical representations of motion had their origins with Galileo, but their algebraic form waited for the 17th and 18th centuries to become standard practice. We’ll make light use of 4 formulas for constantly accelerated motion that relate: $x$ (or actually, $x-x_0 = \Delta x$), $t$ (which is really the interval, $ t-t_0 = \Delta t$ but with the start time as $t_0=0$), $v_0$ (the initial velocity), $v$ (the final velocity), and $a$ (the acceleration).
We’ve not worked out the fourth equation (tax), but it comes from a tedious algebraic elimination of time between the first and third relations. The curves above originally came from these formulae for the particular acceleration, $g=10$ m/s$^2$.
While we owe Galileo for the acceleration due to gravity on earth, his conclusions work for any constantly accelerated object, not just falling. So we would use the general acceleration, $a$ and when we’re dealing with things falling near the Earth, we’d use the specific acceleration.
Let’s work out what the acceleration would be for cars that you may or may not drive.
Acceleration, In Everyday Terms
So far we’ve treated acceleration descriptively: it’s when velocity increases (or decreases) over time. Let’s put this on a more firm footing by defining acceleration as a rate just like we defined velocity:
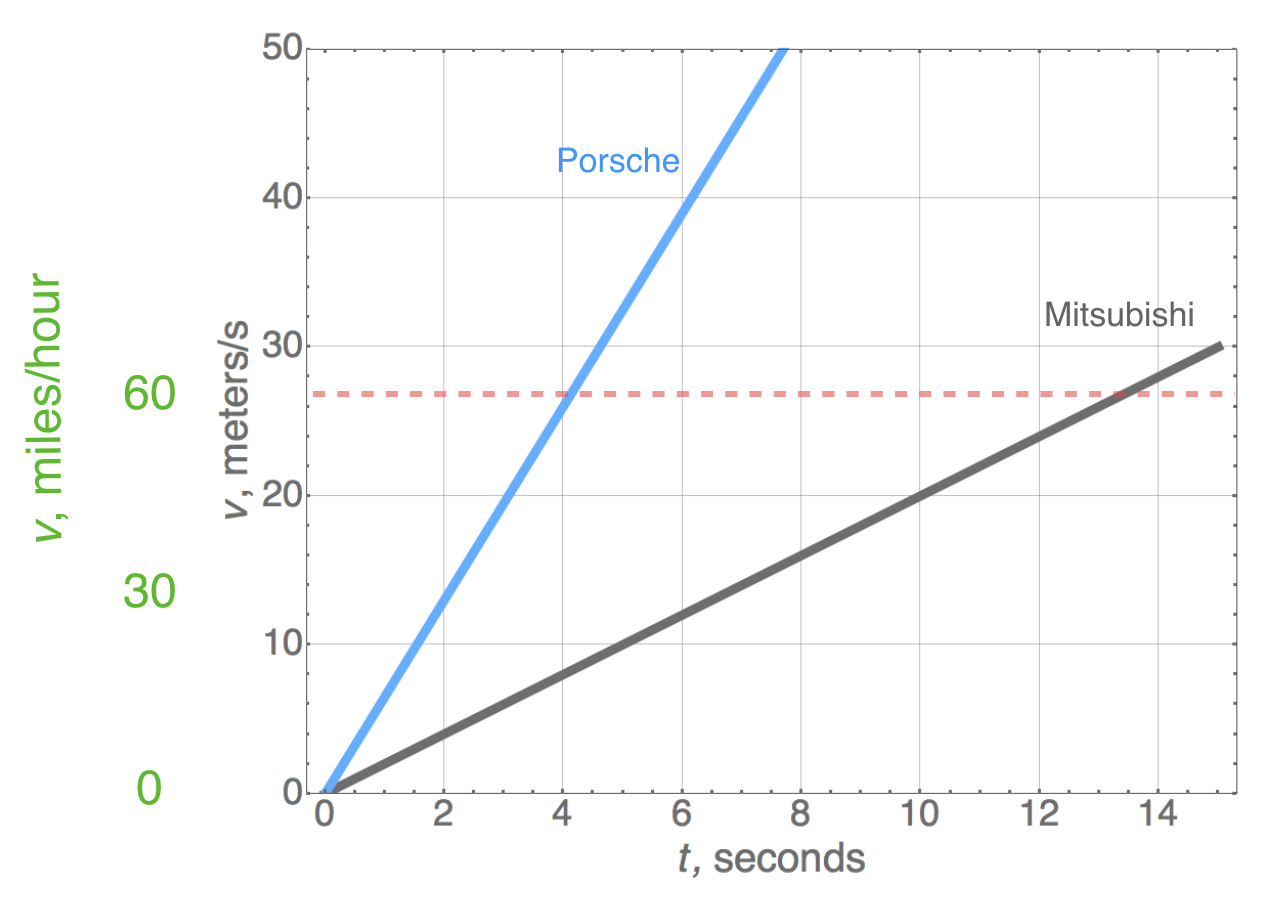
If you own, say, a Mitsubishi Mirage ES, it will take you around 12 seconds to get to sixty from rest. If you own a Porsche 911 Carrera S, it will take you closer to 4 seconds. From our definition we can quote the acceleration of the Mitsubishi as $$\begin{align}a &=\frac{\Delta v}{\Delta t} \nonumber \\ &=\frac{60 \text{ mph}-0\text{ mph}}{12\text{ seconds}-0\text{ seconds}} \nonumber \\ &=5 \text{ mph per second} \nonumber \nonumber \end{align}$$ That odd double time unit, miles per hour per second, shows you that this is a rate...of speed change. If you start from a standing start in your Mitsubishi then after 1 second you will have reached 5 mph and after 2 seconds, 10 mph. Every second, your speed will increase by 5 mph.
While this "mph per second" unit makes it plain, it's not what we would usually say. In physics, we'd convert to a single unit of time and then square it. I'll do this once and then we'll use our own internal unit-conversion machines to convert from one unit to another without the drudgery of forming all of those ratios.
Let’s convert 5 mph into miles per second:
$$\begin{align} X \frac{\text{miles}}{\text{second}} &= 5 \frac{\text{miles}}{\text{hour}}\times \frac{1 \text{ hour}}{60 \text{ min}} \times \frac{1 \text{ min}}{60 \text{ sec}} \nonumber \\ &= 5 \frac{\text{miles}}{\text{second}}\times \frac{1}{3600} \nonumber \\ &=1.3 \times 10^{-3} \text{miles/s} \nonumber \end{align}$$ So our acceleration is $1.3 \times 10^{-3} \text{miles/s}^2$
Wait. I don’t have any idea what that number means in my life!
Glad you asked. Neither do I. It’s an acceleration which isn’t one of our normal everyday units (even though we speed up and slow down all the time while walking and driving). But one acceleration we do have a feel for is that of gravity, so let’s compare it to little gee, $g$.
This doesn’t exactly press you to the back of your seat. You know how I know that? Because we can further convert it to something that we can compare with falling. That is, compare it to little $g$ which we know to be about $10$ m/s$^2$. So let’s get the miles per second into meters per second and we’ll just a little engine to do that.
We know:
- our acceleration is $1.3 \times 10^{-3} \text{miles/s/s}$
- we can change the miles into meters and we’d then have that acceleration in meters per second per second
🖥️ Please answer a question:
we find that our unenlightened Mitsubishi acceleration of $1.3 \times 10^{-3} \text{miles/s}^2$ converts to $2.2$ m/s$^2$. One more step to get it into something we can compare with life.
pulling gees
Acceleration at a rate of $g$ is called…well, “gees.” And “pulling gees” is a measure of acceleration that fighter pilots (and NASCAR drivers) must contend with: in order to not black out, humans can tolerate accelerations up to around 6 $g$’s, or accelerations of $6 \times 9.8$ m/s$^2=$ about 60 m/s$^2.$ That’s moving right along as you will see from the Porsche-experience below.
Remembering that $g=32 \text { ft/s}^2 = 9.8 \text{ m/s}^2$ we realize that flooring the little Mitsubishi isn’t exactly like falling off a log…or falling off of anything for that matter, since it’s more than 4 times less acceleration than falling off that log at $g$ (9.8/2.2 = 4.4) . If you black out while speeding up in your Mitsubishi, it’s not because of acceleration.
Graphical Kinematics
Here’s what our two cars’ accelerations look like plotted:
Completing our journey through the graphical representations of constantly accelerated motion, here’s the quadratic relation of the distance that the Mitsubishi and Porsche travel as a function of time:
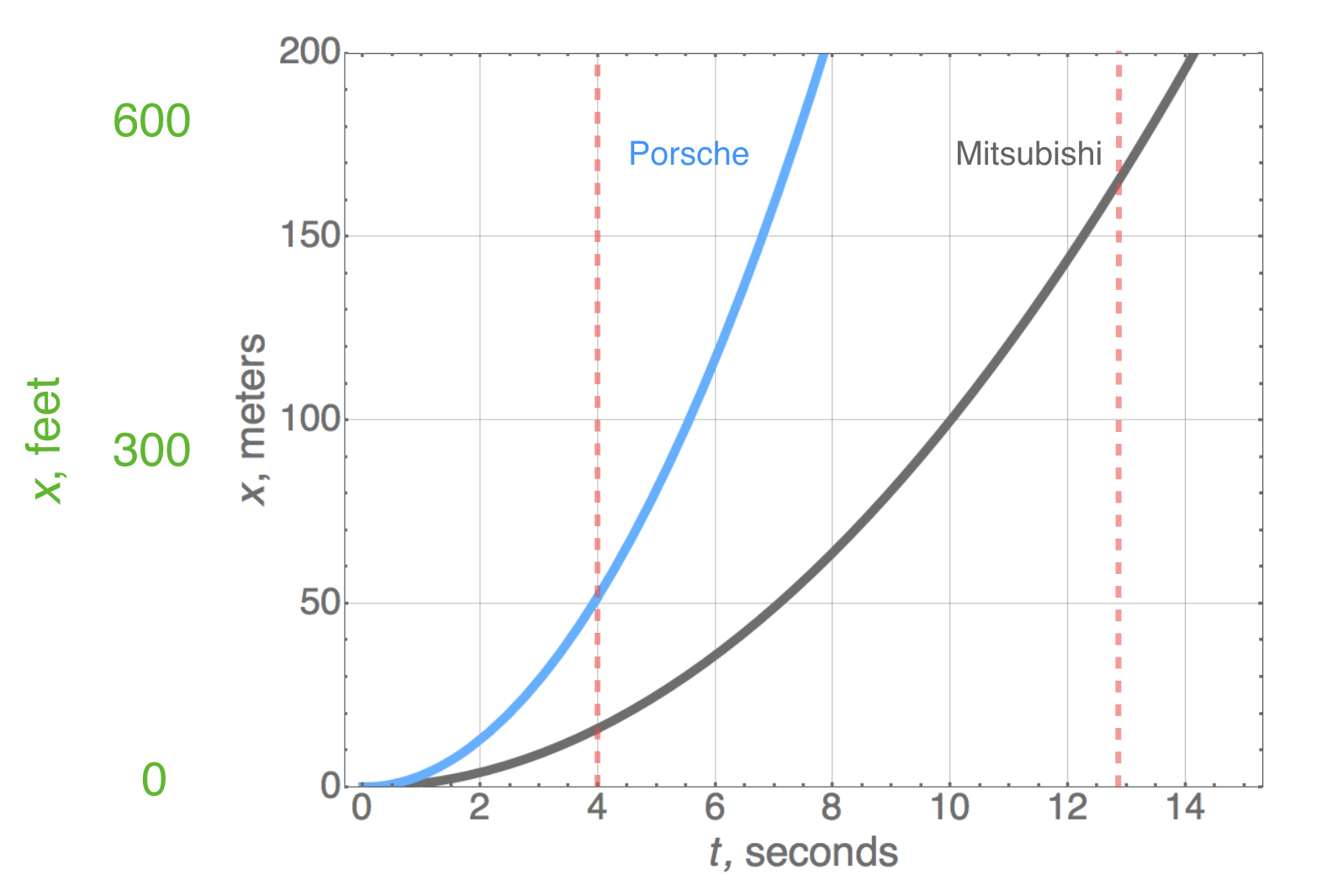
🖥️ Please answer a question:
Finally, we can compare distance versus speed for our two cars.
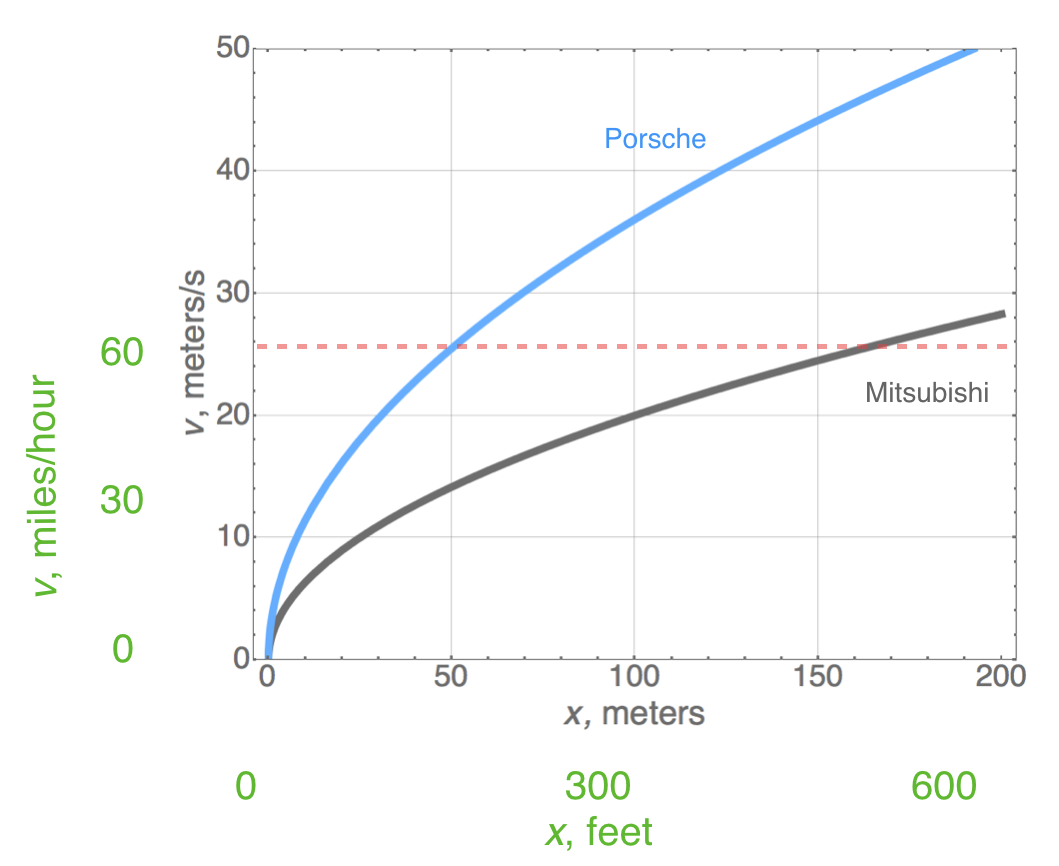
Special Kinds of Acceleration
Now we can categorize acceleration into three separate categories.
Zero Acceleration
No acceleration indicates that an object maintains a constant velocity.
Positive and Negative Acceleration
Positive and Negative accelerations mean very different things here and we’ll illustrate this with a simple pair of examples. When you leave the city limits, your speed goes from 35 mph to 55 mph, so the numerator in the definition of acceleration in Eq. \eqref{acceleration} and this would be a positive acceleration (when you divide by the time it takes), or just “accelerating.”
But when you come into town from the highway, your speed goes from 55 mph to 35 mph and the numerator in the acceleration equation would be a negative acceleration, which is called a deceleration. So acceleration is negative or positive by virtue of whether the object is slowing down or speeding up.
Let’s look at a deceleration plus we’ll include an initial velocity. On the water.
USS Nimitz
The USS Nimitz The USS Nimitz is the lead ship in the supercarrier class in the US Navy. It carries 3200 sailors and aviators and supports nearly 100 fixed wing aircraft. The Nimitz has a top speed that’s classified, but it is at least 30 knots (34 mph). Suppose it was cruising at that speed in open water and came to a complete stop (an unusual maneuver) in 30 minutes, what would be its deceleration if it’s constant?
What do we know:
That makes sense, right? It would be negative, since it’s decelerating. It’s a tiny deceleration because it takes so long for it to stop (which is in turn because an aircraft carrier is a really heavy thing!).
Varying Acceleration
When you accelerate in your car, you probably press on the accelerator pedal more and more. If you held it constant and ignored wind resistance, you’d accelerate at a constant rate. But if you press harder and harder, you’re varying the acceleration…a non-constant acceleration. This is a more complex problem mathematically, so we’ll not go there. But it’s a very common occurrence.
Cars are not the only place where we encounter non-constant accelerated motion. How about running? A sprinter comes out of the blocks with a very high change of speed, and so a very high acceleration. As she gets into her stride and become more erect, her effort must fight against wind resistance and besides, her internal quick expenditure of energy would be hard to maintain, so there’s a reduction of acceleration. Note this doesn’t mean a reduction in velocity, just that the velocity increases at a slower rate as the race goes on. Nor does it mean a deceleration, rather she’s still going faster, just at a lesser rate than before.
The Pendulum
A pendulum is a trivial toy, yet it uses many key ideas about motion and force. Galileo, Christiaan Huygens (whom we’ll meet in a bit), and Isaac Newton each made many pendulums and did extensive experiments with them. Because of its immediate simplicity, quantitative measurements are easily done with modest tools. This figure is a picture of a simple pendulum which I’ll refer to periodically over the next few chapters.
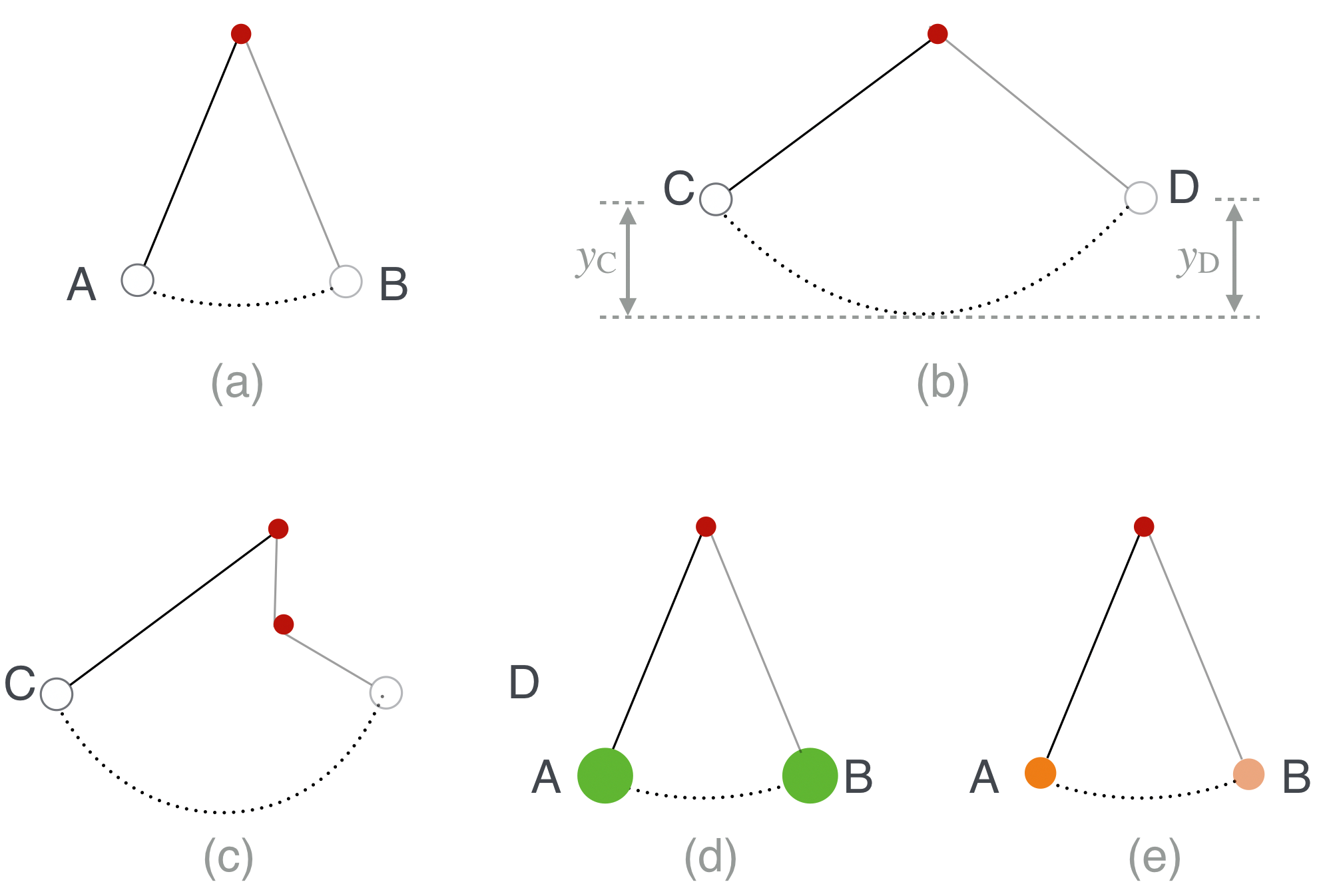
Buzzword: a “period” is the time that it takes for some repetitive motion to repeat.
These are all observations that Galileo made about pendulums in 1602. In (a) the little pendulum bob makes a to-and-fro motion from A to B and then back to A and the same thing happens in figure (b). Galileo found that the time to complete a full period (from A-B-A, and from C-D-C) was the same for (a) as it was for (b).7 This is called the isochronous (equal time) behavior of pendulums.8 It doesn’t matter how far up you start the pendulum, the time it takes is the same for all. In fact, he found that the period of a pendulum depends only on the length of the cord.
The next thing that he found was close, but not quite the case, but here he was again, very clever. Look at (b) which has some additional markings. In the drawing the height that the bob starts from at C, $y_C$, is the same as the height that the pendulum goes to at D, namely $y_C=y_D$. Furthermore, this common height is regained, back and forth as the pendulum repeats its motion. Except it doesn’t!
Real pendulums don’t do this—they slow down. Galileo acknowledged this observation. But instead of believing that every pendulum swing for different bobs to be unique, he claimed that there was an unchanging—and unobservable—rule of motion (a “law”) that’s masked by friction and air resistance.
This is an example of the most important idea that Galileo left for us, even more important than some of his discovered facts about Nature:
the real-rules of nature are hidden
Galileo decided that the regularities of Nature were ideal and hidden from actual behavior. We can get close, but not exactly there. An ideal pendulum would repeat forever, always coming back to those original heights and it’s friction in the pin and air resistance that modify that perfect behavior. The goal of natural philosophy (our “science”) is not to describe what we observe in real life, but rather to uncover those hidden regularities and then explain the corrupted behavior that we observer as due to small influences like friction. Without this new motivation, physics is impossible.
Galileo studied this return-to-the-source phenomenon by sticking a peg in the way of the string causing the bob to quickly rise…back to that same level as shown in figure (c).
Finally, here’s one more important discovery. Figures (d) and (e) are meant to represent the comparison of two pendulums for which the bobs are different masses and/or different materials. Through experiment he found that they behave identically. Nature doesn’t care if the big pendulum bob is iron and the other is wood: the bobs have the same periods and behave the same regardless of their nature.
We’ve just crossed an important historical milestone. Physics is now possible because of this crucial discovery by Galileo: there are fundamental rules that nature follows, common for all processes but hidden from our observations by disruptive effects like friction and air resistance.
The physicist’s job is to find these hidden, universal rules by conceptual and mathematical modeling.
Everything that follows in this book is built on this commitment!
Back to falling bodies
It’s this extrapolation from pendulum motion to falling bodies that led him to decide that a falling body accelerates the same regardless of its size, material, or weight.
There are two really important ideas here. First, as I emphasized he’s assuming that the true rules of motion are ideal and hidden from us in real life. Second, he explains the observational fact that a heavier object when dropped will fall to the ground faster than a light object. Your eyes deceive you! He surmised that the lighter object is much more affected by air resistance than a heavier one. Even if an object was the same material, but different shapes—they should land at the same time, but in real life the air would slow down the larger of the two. This is pendulum-thinking! He saw a connection between one phenomenon (pendulum periodic motion) and a seemingly different phenomenon (free fall) and used one to gain insight into the other. To Aristotle, one would be unnatural motion and the other natural, so this is a big leap.
He never in his life—nor have you or I—ever seen two different objects fall in the presence of gravity in exactly the way that Galileo insisted was the underlying rule. Humankind had to go to the Moon in order to test this in the complete absence of any air:
In 1971 towards the end of his last moon-walk, Commander David Scott dropped a hammer and a feather in order to demonstrate (test?) Galileo’s assertion about free-fall. Scott was an engineering student at the University of Michigan for one year (and was on the swim team) when he transferred to West Point. He graduated with such high grades that he was able to pick which service to join and chose the Air Force where he became a test pilot. Apollo 15 was the fourth moon landing and Scott’s third space mission.
But wait, there’s more. In an ingenuous blending of pendulum and inclined plane motion, he discovered Newton’s First Law of Motion, 60 years before Newton did. :) This figure tells that story:
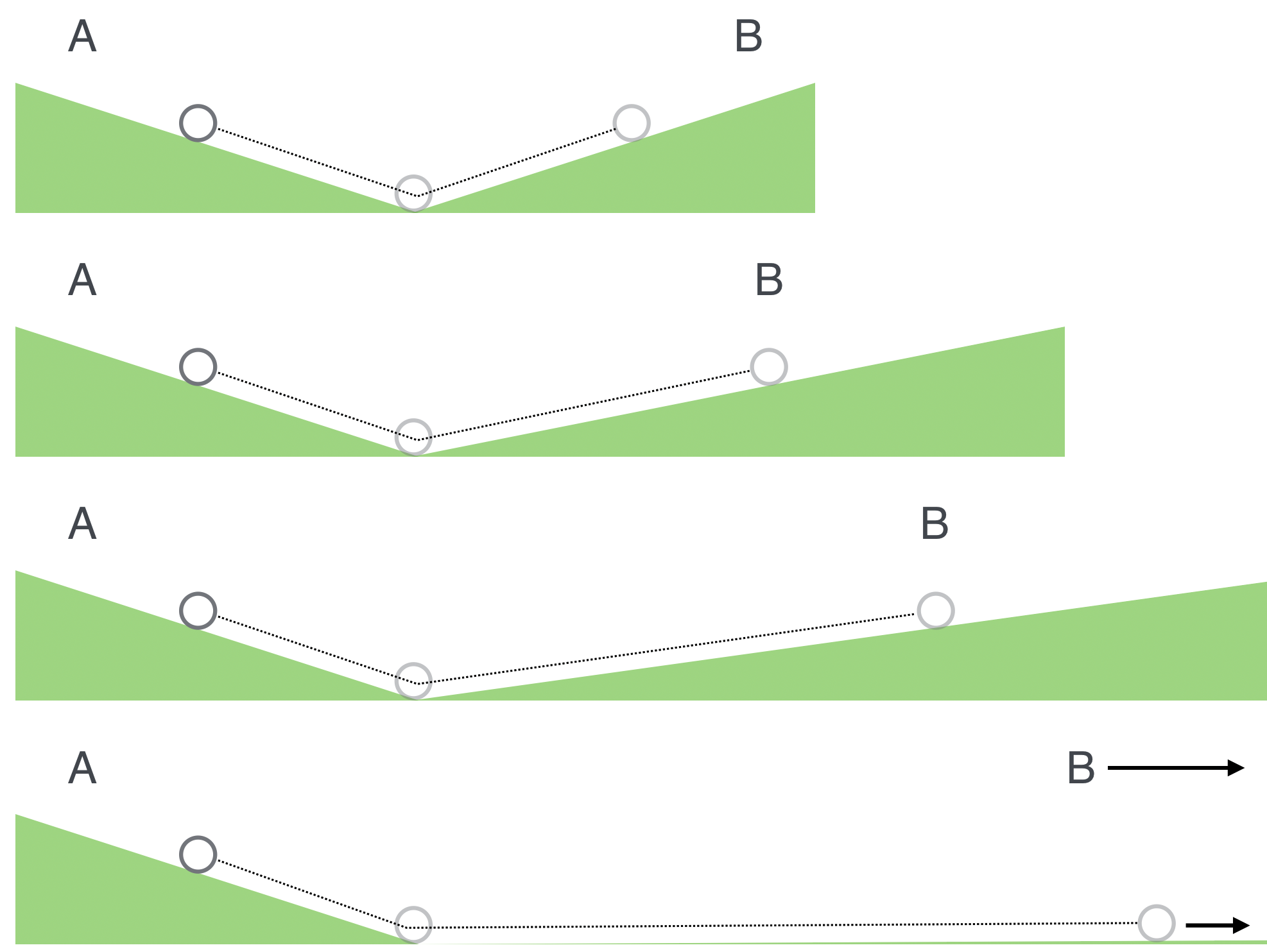
In the top figure, a ball rolling down an inclined plane gets to the bottom and rolls up the adjacent plane to B which is at the same height as A. In the next figure the second plane is shallower, but the ball still makes it back to its new B…which is at the same height. The next figure, the same thing happens. Galileo then says what if the adjacent incline is not an incline at all, but just a flat surface—his conclusion was that the ball would continue in a straight line forever. 9
Again this conclusion is totally contra-Aristotle! There’s no pushing involved in this final motion. Once it’s started, it goes. Notice how far behind Aristotle looks in Galileo’s rear view mirror! He’s not worried about natural or unnatural motion and he’s not concerned himself with why the motion continues. Rather he’s asking different questions…How questions rather than Why questions. Aristotle’s students would start with a philosophical prejudice and interpret what they saw in accordance with that philosophical system. Why did something in Nature happen? Aristotle’s writings would provide the answer, regardless of the contortions required to make it fit. The authority of Aristotle functioned much like legal precedent functions in a courtroom: you explain according to textual authority. Nope. Not our Galileo, not in our science.
Galileo threw all of that aside and observed nature with fewer (albeit, different) preconceived notions than people before him. So if you release a ball in any of our three examples—free fall, pendulum, and inclined planes—where would it go? is his question. Not, why would it go. He’d set up the circumstance and he’d observe it—no Aristotelian would do an experiment. They would think about it in the specific context of the philosophy and passively observe.
Now he’s doing physics. Aristotle has left the building.
Air Resistance
Little $g$ is a large acceleration, but raindrops don’t usually bruise us and hail stones don’t usually kill. Were there not for air resistance, nice spring showers would be dangerous as rain drops fall a long way! It turns out that things dropped from high up reach a speed in which the viscous drag of air friction pushes back with the same force that the Earth pulls, causing a falling object to reach equilibrium. The result is that the speed of falling becomes constant to what’s now called the Terminal Velocity, which depends on an object’s size.
For example, a regulation major league baseball will reach terminal velocity in about two and a half seconds after falling about 100 ft. At that point, its speed will be just a little more than 60 mph and will stay at that value. For reference, the “Green Monster” left field wall in Fenway Park is about 40 feet (11 m) high, so you can see that high fly balls would be high enough to reach terminal velocity on their way down.
While Galileo was on the faculty at Padua, he did other experiments with motion which lay dormant until in 1638 he wrote the second of his great books, Discourses and Mathematical Demonstrations Relating to Two New Sciences. He finished this work while in house arrest outside of Florence as an old, sick man. How he got into trouble is a story that we’ll leave for our discussion of early astronomy.
That Tower

You know the one. That story. Galileo did write about dropping two cannon balls from the Leaning Tower of Pisa and he described what one would see: the lighter of the two would lag the heavier. Not simultaneous. He’d seen things fall and realized that the density of the ball compared with the density of air would favor the more dense object. But he was committed to the program and explained the lack of simultaneity was due to the environment. The rule of free fall was still valid as an abstraction. Here’s what Galileo said:
Aristotle says that ‘an iron ball of one hundred pounds falling from a height of one hundred cubits reaches the ground before a one-pound ball has fallen a single cubit.’ I say that they arrive at the same time. You find, on making the experiment, that the larger outstrips the smaller by two finger-breadths, that is, when the larger has reached the ground, the other is short of it by two finger-breadths.
One hundred cubits is about 200 feet. The Leaning Tower is 58 meters high, or about 190 feet, so roughly 100 cubits.
Galileo was right to scorn the enormous difference in distance fallen predicted by Aristotle but his own prediction is way off!
That “two finger breadths” would be only a couple of inches at most. However, if one uses a model of air and iron and calculates the effect of the retardation of each by the medium, you find that the lighter would lag the heavier by about 4 feet! So he didn’t perform the experiment since he could easily have observed that separation. Many have since, confirming the calculations.
Also one would have thought that such a demonstration would have been a big deal on “campus” and Pisa would have been all abuzz. Certainly there are lots of painted depictions of the event. But there is no correspondence, no public announcement or public report…silence. This is another of the myths created by Galileo’s devoted and imaginative student, Viviani. The experiment at the tower and elsewhere was performed by others, including: Vicenzio Renieri, Giorgio Coresio, Simon Stevin, Giuseppe Moletti, Varchi, and John Philoponus. Reniere was a professor and priest and reported the results (apparently badly) to Galileo. Maybe that’s where he got the idea.
In the absence of air resistance, a cannonball—or an apple—would fall the 58 meters to a speed of about 33 m/s, about 70 mph. And now you know how to calculate that.
Going In the Right Direction!
Now we need to add one more piece to the modern story. As we saw in the Mathematics review lesson, distances—displacements—are vector quantities. Because distance is in the definition of velocity, and since distance is a vector, so is velocity. Since velocity is a vector and acceleration is defined in terms of it? Yes, acceleration is a vector too.
Velocity Is a Vector
Here’s our first physics-vector. I’ve been loose with the words speed and velocity. In fact, there’s a difference: velocity is a vector, $\vec{v}$, and so it includes a magnitude and a direction, and the magnitude of velocity is the speed. Now the definition of velocity should really be:
implicitly included distance ($\vec{x}$) as a vector quantity, but not time. North and east are different directions and $\vec{x}$ makes that clear. Like mass, temperature, and many other quantities, time is not a vector. At least, not yet!
Likewise, 60 mph east is not the same velocity as 60 mph north, but the speeds are the same–your speedometer would report the same speed for both trips. Certainly if you’re trying to go north, you don’t want to deploy a velocity that points east. So both the magnitude (speed, here) and the direction are required to specify a velocity. We simply draw an arrow (on a paper, or map), the direction of which points in the direction of travel and the length of which is defined by some scale of speed magnitudes.
Now when you’re out walking I want for you to invent your own speed scale—how many inches equals 1 mph of walking speed—and then imagine this arrow sticking out of your chest. As you speed up, the arrow gets longer and as you slow down, the arrow shrinks. If you turn left, the arrow turns with you. Everywhere you go, you imagine your very own velocity arrow preceding you, pointing the way. You should also imagine arrows coming out of everyone you see, people on bicycles would have longer arrows and cars would have even longer ones. When they come to a stop sign? The arrow shrinks as you decelerate and blinks out of sight. Keep this in mind as we move on to those length-changing arrows.
Acceleration Is a Vector
Since velocity is a vector and acceleration is defined in terms of velocity, it too is a vector:
While the little arrow that represents your personal velocity always points out in front of you, its direction seems rather arbitrary. It goes where you go, but there’s nothing special about the direction. But that’s not really the case since our movement is inside of a coordinate system of streets, sidewalks, hallways, etc. and they all have relative directions and we could describe our velocity in terms of them. So, “60 mph east” would be a perfectly good vector description of speeding towards Detroit from East Lansing. Likewise, if we defined a vector of unit-length ($\mathbf{i}$) that points in the east direction and call that the $x$ axis, that same velocity could be written as $\mathbf{v}=60\, \mathbf{i}$ mph. The pretty subject of vector analysis is built this way, but in QS&BB we won’t use that notation. We’ll be relaxed and laid-back about most vectors.
In that spirit let’s choose to define our coordinate system such east is the positive direction and west, a negative direction. If you’re walking east, then you could say your velocity is 2 mph, east, or you could say that your velocity is +2 mph E. If you’re walking to the west, your velocity would be -2 mph E or +2 mph W (but usually we assign a positive direction and stick with it…East, to the right, is standard). The direction and the sign are mingled. Because we will work in one dimension most of the time, this dual-role for a sign will matter but hopefully be pretty easy and we will almost always be able to say: east is the $x$ axis and so our velocities above are +2 or -2, with the sign implying the direction of positive $x$ is east.
This figure lays out the circumstances for constant acceleration, including zero acceleration.
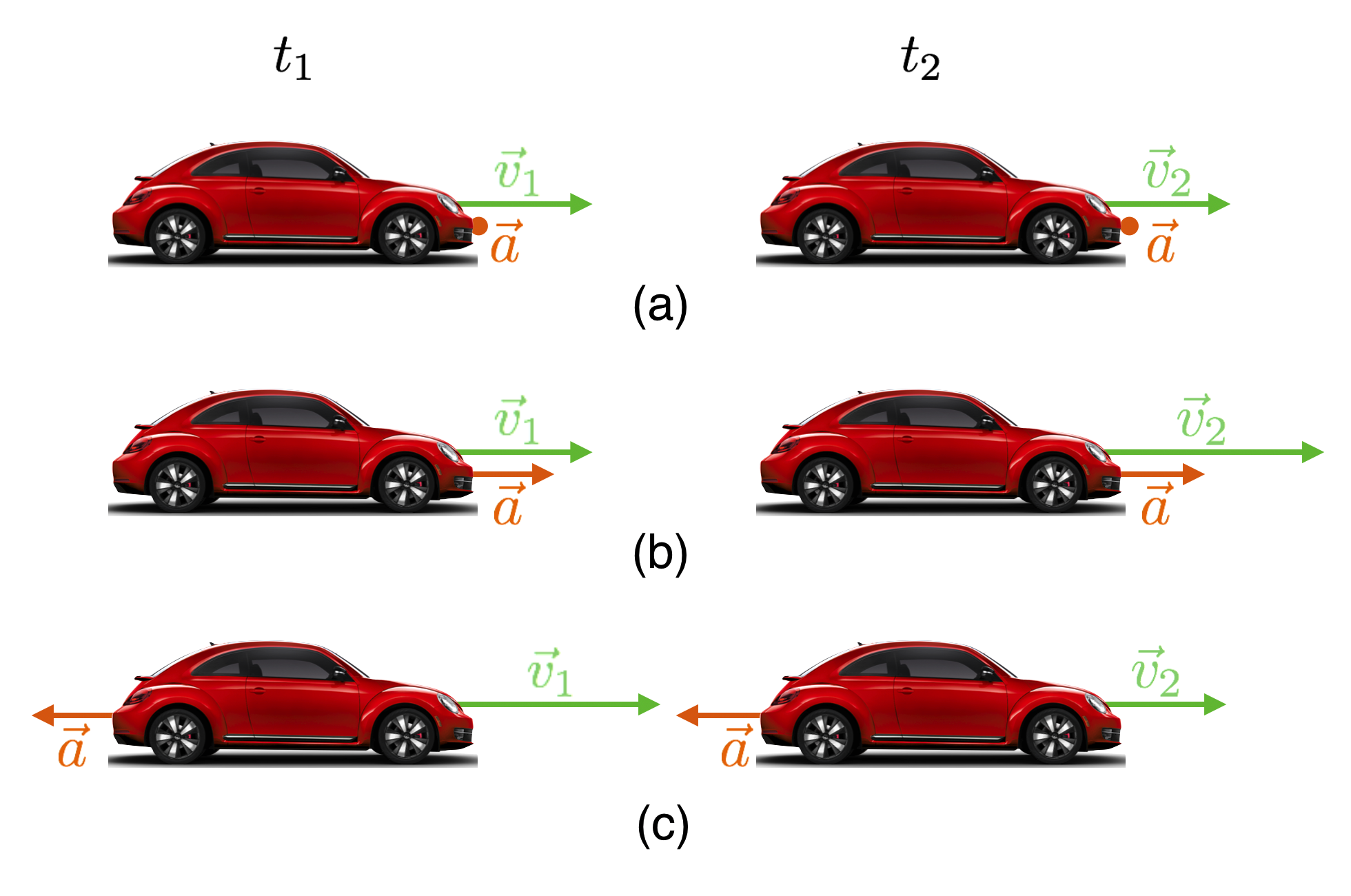
Of course the two vectors for velocity and acceleration would each refer to their own scales. At a constant speed, the velocity vectors are identical at the two times and the acceleration vector has zero length. As the car accelerates, the velocity vector gets longer. As the car decelerates, it’s still going to the right, but its velocity vector gets shorter. The acceleration vector points the other way, so deceleration vectors point in the opposite direction as the velocity vectors.
I defy you now to not see arrows coming out of everything around you that moves. Welcome to my world.
What Goes Up, Must Come Down
Armed with Galileo’s discovery and our notion of vectors, the acceleration felt by all falling objects near the Earth is constant, we can look at some examples. Let’s drop something from the Leaning Tower, in honor of fictional accounts of famous scientists. Like an apple. After all, Galileo showed that the kind of fruit—or cannonball—didn’t matter. We’ll stick with an apple.
Mr. Google tells me that the height of the Leaning Tower is 183 ft. By now, you know how to convert that to meters and it’s 57 m. Let’s ignore air resistance for a moment and look at the figures in Section 5.3 above for distance versus time and velocity versus time for an acceleration of $g=10$m/s$^2$.
Let’s make contact with real life: how quickly does the apple take to hit the ground and how fast is it going in m/s? How fast in mph?
🖥️ Please answer a question:
That speed is just about a high school fast ball, barely over the terminal velocity.
🖥️ Please answer a question:
Projectiles
Throwing things was hard to understand.
projectiles, Aristotle’s way
Where Aristotle got himself into big trouble was with projectiles, like a thrown spear. His philosophical system came before explanation so he had to do an embarrassing dance to explain that when a rock was thrown the continuous “push” that he insisted was needed came from the displaced air rushing around behind the rock and pushing it forwards. Seriously. Everyone knew that this was nonsense. How can you throw a pointed spear sharp end first and then blunt end first? His authority was absolute, and organization of the first medieval universities with Philosophers and Theologians at the top guaranteed that natural science was taught by them. Mathematicians and astronomers had supporting roles that were aimed at more mundane activities like casting horoscopes and designing military weaponry and fortifications.
Although we’ve been dealing with 1-dimensional motion, Galileo wasn’t done when he figured out that everything falls at the same, constant acceleration of gravity. He also tackled the other problem that Aristotle messed up: throwing something. With an understanding that objects would happily move at a constant speed without being pushed (his two inclined planes) and that objects fall towards Earth with a common acceleration, he had the genius idea to embed these two different motions together into the motion of a single, thrown object. Let’s follow his experiment by looking at his notes in the figure below.
What you see are various measurements of rolling a ball off the surface of a table and marking where it lands according to how fast it was going. How did he repeat measurements so that each attempt would be the same speed upon lift-off? He rolled them from an inclined plane where he could dial-up the speed he wanted by how far up the plane he let go of the ball as shown in this figure, again from Galileo’s notes:
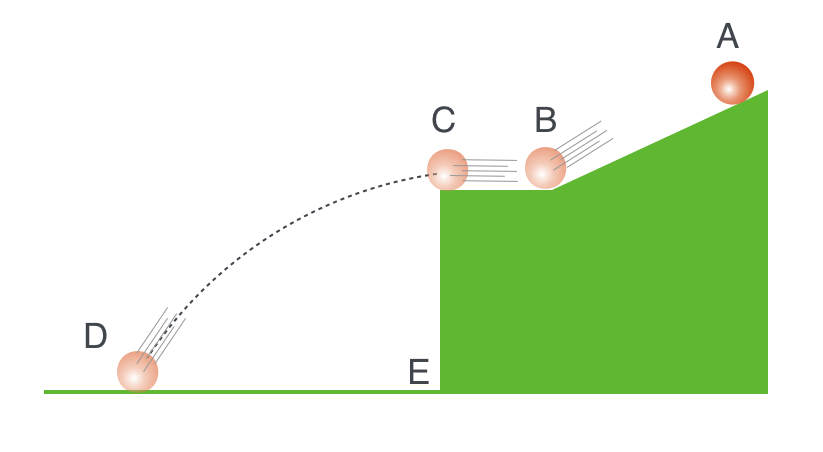
Clever, no? So let’s think like he did. If the speed of the ball at B is $v_x$, then what’s the speed of the ball just at the edge of the table, C? It would be the same, which we’ll call $v_x$. Now when the ball flies off into space it acquires two separate motions that are combined: the ball continues to have the unchanged horizontal speed, $v_x$. But as it falls, it starts to acquire a new vertical motion, because it’s now accelerated down at a rate of $g$. The two motions are separate, but together! So throughout the trajectory, the ball’s horizontal speed remains $v_x$. Nothing has happened to change that. The ball’s vertical speed increases as the ball “falls” along this curved path.
Now here’s the neat thing. Suppose at the same point where the ball leaves the table, another ball is allowed to just drop from that point, say at point C in the second figure above so that it falls (only under the influence of gravity!) to point E. This one has only one kind of motion, vertical and accelerated. In fact, it’s accelerated by the same amount as the first one and from the same vertical height, at the same time. So which one reaches the floor first? They both reach the floor at the same time.
This bundling up of two separate motions into one object was inspired reasoning. Nobody had ever conceived of that sort of thing. By analyzing the landing point and some sophisticated solid geometry, he was able to extrapolate to perfect conditions and assert that the trajectory that the ball—any projectile, a cannonball, a spear, an arrow—followed was that of a parabola.
The Beginning of Physics
When Galileo reached the conclusion that all objects fall to Earth with the same acceleration, he was going against what he—and Aristotle, and everyone else—actually observed. Let’s review the number of Galilean ideas that we’ve encountered…all of which were overthrows of the Aristotelean—and hence Catholic—dogma.
- To understand nature one must do experiments.
- To understand nature, one may not defer to authority, like the Bible or Aristotle’s writings.
- For a pendulum: the period of two pendulums of the same length, but started at different heights will have the same period.
- For a pendulum: the period of two pendulums of the same length, but different materials will have the same period.
- For a pendulum: the period of two pendulums of the same length, but different masses will have the same period.
- In free-fall: two objects of different sizes but of the same material would reach the ground at the same time.
- In free-fall: two objects of the same size but of the different mass would reach the ground at the same time.
- An object already moving in a horizontal direction will never stop and will not require an active pusher.
- Any object, regardless of material or mass, if thrown as a projectile will execute a parabolic path and will not require an active pusher.
- A whole bunch of astronomical observations and conclusions that we’ll talk about later!
Each of these requires that there is no resistive medium affecting the motions. So each is a discovery that cannot be shown to be absolutely the case on earth. Yet each is a statement reflecting what we now know are fully-trustworthy rules about nature.
Let’s visit the Matrix.
The Red Pill, or the Blue Pill?
This is very un-Aristotle. First of all, Aristotle would never have countenanced doing experiments. You can look at Nature, but don’t touch. But Galileo was all about constructing experiments and making quantitative measurements of what he observed. This was largely new and recognizably “modern.” But there’s more. To him Nature’s rules are hidden to us. We can get close to them by reducing marginal effects like friction but then we have to extrapolate from what we see in our rough and ready laboratory to the hidden rules of a more perfect world. The pendulum bob gets close when it swings back, but the actual rule driving the motion would instruct the pendulum bob to come all the way back to the original height. That’s what’s real.
I cannot over-emphasize how important this is. This is very much Plato’s view of nature, not Aristotle’s. For Plato, The Real was perfect and with our poor, corrupt visual tools we can only perceive inferior copies of the real things—Platonic Ideals. While there is much that’s wrong with Plato’s philosophy, the uncovering of nature’s hidden order—free of imperfection—is the goal of modern science.
The Father of Physics
Nobody had ever done what Galileo did in all of history. Let’s summarize his strategies:
First, Galileo chose not to explain nature (motion in his case) on the basis of logical argument from within pre-conditioned philosophy (neither Aristotle’s nor the Church’s): Galileo confronted nature without precondition: he assumed that Authority did not dictate how the physical world behaves.
Second, rather than sit passively and observe, Galileo created artificial circumstances designed to explore particular questions: he assumed that Nature can be characterized by doing experiments.
Third, rather than report results as a narrative, Galileo made quantitative measurements under the assumption that arithmetical and geometrical constructions were the appropriate way to describe physical behavior. This idea that nature appears to behave according to mathematics is not new (going back to at least Pythagoras) and is the bedrock of modern physics. We don’t understand why the universe is so understandably mathematical!
The first three strategies alone would make Galileo one of the first, great scientists. But he went further, and his Physics Paternity comes from his Platonism.
Fourth, Galileo chose to interpret nature as consisting of rules that can only be discovered by going beyond the rough regularities that we always see in our observations. Nature is best assumed to be simple and mathematical, but all that we can observe is complicated by extraneous effects and the true nature…um, of nature is hidden, just out of grasp. Strip away complications like friction as best you can and through mathematical modeling and extrapolation we can uncover nature’s hidden rules.
Without this fourth strategy, physics would be impossible.
The rules of nature are often hidden from experiment and must be inferred by a combination of theoretical modeling and experimental confirmation.
Taken together, these four strategies form the modern-looking Nature of physics.
What to Remember from Lesson 4?
This has been all about motion without regard to its cause. In a slightly different order from how it was presented, we have a model of constantly accelerated motion (which is an approximation for real-world events).
The speed of a body is proportional to the time elapsed.
The distance traveled by an object undergoing constant acceleration is proportional to the square of the time elapsed.
The distance and the speed are related through a square root.
In all of these relations, if there is no acceleration, then the $a$’s above are zero.
Acceleration near the Earth.
Galileo’s major contribution to the study of motion was his experiment that showed the above quadratic relation between distance and time. His work focused solely on a particular acceleration, namely that of gravity near the surface of the Earth. That particular value is important enough that it gets its own name, which we affectionately call “little $g$”:
In this work he showed that neither the nature of the material nor the mass of a moving object affects these motions.
Projectile motion
Galileo also demonstrated that an object thrown at an inclination to the Earth’s surface executes a parabolic path with the horizontal component of the object’s velocity unchanging and the vertical component of the object’s velocity decelerating according to $g$ up and accelerating according to $g$ down.
Pendulum Motion
Galileo also found that the frequency that a pendulum repeats back and forth (its period) is independent of how high up the pendulum bob is released and independent of either the mass or material of the pendulum bob. He found that the only quantity that governed this motion is the length of the string. Historically, this has been called Galileo’s Pendulum…law.
What Physics Is
Each of the above models are an approximation to circumstances in which there is no air resistance or friction. This means that these relations tell a story about how things move in an ideal sense. This, Galileo taught us, is the goal of physics: understand and mathematically model the basic rules of nature in ideal circumstances and then add successive “drops” of reality (like friction or air resistance) depending on the goal of one’s modeling.
-
He wrote low poetry making fun of them and their sometimes affection for brothels. ↩︎
-
There were a number of other issues with his physics, like his “four causes” which made things move because they had some desire to find a natural place. But we’ll not go there. Okay. I’ll go there a little. Motion was not only for moving objects in space. A cat growing into a kitten was a form of motion. A seed growing into a plant was a form of motion and the seed’s desire was to reach that plant-ness as a matter of fulfillment. Now take this into the kind of motion that we care about—his Locomotion—and you’ll see why I didn’t go there. Much. ↩︎
-
This is often attributed to Einstein, Woody Allen, and John Wheeler! It actually comes from Ray Cummings’ short story The Time Professor from 1921. Stick with me. You’ll learn all sorts of odd facts. ↩︎
-
So if class starts at 10:20 AM and if I were to fall asleep in mid-sentence at 10:50, it would be embarrassing. When you posted my snoring image to Instagram you’d calculate that $t_0=10:20$ and $t=10:50$ and so you’d report that I managed to stay awake for $\Delta t=t - t_0 = 30$ minutes. ↩︎
-
This term will have a more specific definition when we meet Mr Einstein. ↩︎
-
Actually…this was before there was an “Italy.” ↩︎
-
This is strictly true for only small angles which was not understood for 50 years. ↩︎
-
So is it pendulums or pendula? My Latin teacher would say the second, but standard usage accepts the former. We’ll be standard. Besides, I didn’t especially like my Latin teacher. ↩︎
-
Actually, here he was confused. His “straight line” would have followed the curvature of the earth’s surface. So not Newton’s “straight line.” ↩︎


