Lesson 11 Charge It! Charges and Magnets
Electric charges, magnets, and currents.
11.1 Contents
11.2 Goals of this lesson:
- I’d like you to Understand:
How to calculate forces on charges using Coulomb’s Law
How to determine the direction of magnetic force due to a current
How to calculate the numbers of charged particles corresponding to a total charge in Coulombs
- I’d like you to Appreciate:
The effects that parallel currents have on one another
The similarities between a loop of current and a magnet
That the Earth is a magnet and what are the north and south magnetic poles
- I’d like you to become Familiar With:
The role of Gilbert in the history of physics
The contributions of Franklin to electricity and magnetism
11.3 A Little of Gilbert
William Gilbert was born into a middle class family during a period of relative calm following the turbulence of Henry VIII’s reign and the future civil war in the early 17th century. During that century, Britain reorganized its entire society with the confiscation of Church properties, secularization of public education, and subsequent increase in general wealth and a middle class. London quadrupled in size and became an international center of trade and hub for British exploration of the Americas and East India. Gilbert’s father was a benefactor, serving as a prominent lawyer and benefited from these changes. Gilbert’s life was spent in civil service as both physician and private scientist, outside of a university. His was an illustrious career, subsequently serving as President of the Royal College of Physicians and the personal physician to Queen Elizabeth I and subsequently James VI as well.
Gilbert was born a year after Copernicus died (coinciding with the publication of De Revolutionibus) and a year before the Catholic Church’s Council of Trent was seated to try to recover after the simultaneous loss of influence in England (with Henry VIII) and Northern Europe (with Luther). Little is known of Gilbert’s early years, but for his education in his family’s home town of Colchester and subsequent study at St John’s College, Cambridge. There he took his medical training and absorbed, like everyone, the Aristotelianism that passed for advanced learning…and like his famous contemporaries, he rejected it in order to make intellectual room for a more reliable understanding of nature. Like Galileo, he taught Aristotle for a while as a “Master” at Cambridge, but like Galileo after him, he became convinced that the only route to understanding nature was through observation and experiment—not through appeal to authority and ancient writings. Unlike in Galileo’s Italy, Britain was now free of the Church and its authority over what could and could not be written about.
Gilbert died in 1603 of bubonic plague and many of his personal effects were burned so we lack a detailed understanding of his life and research. We know that he never married and of course know of his professional success. His definitive book, De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure (On the Magnet, Magnetic Bodies, and the Great Magnet of the Earth, 1600, aka De Magnete) is enlightening and shows perhaps the first true experimental scientist at work. A relative (his brother?) later collected unpublished notes into a posthumous book, De Mundo, which shows a thinker, like Copernicus, with one foot in Medieval traditions and the other in modern times. Ironically, fire during the London “Great” plague of 1665 destroyed Gilbert’s London home as well as the library of the Royal College of Physicians where Gilbert had bequeathed many of his papers, so the second recurrence of that terrible disease in London spawned Newton’s imaginative scientific genius, but destroyed the last bits of Gilbert’s history.
At some point Gilbert became interested in both magnetism and electricity. Both were similarly magical and both magnetic and electrical effects seem to create forces without any intervening medium—without contact. Little was known, but much mysticism was invested in magnetism, especially. Rather than relying on hocus-pocus descriptions or ancient Greek authority, Gilbert set about to systematically study what materials were specifically influenced by magnets and what by static electricity. The Greeks and Chinese had discovered “Lodestones” which we know today to be a naturally magnetized minerals and both cultures had found that small iron magnets, when floated on water, would align themselves in a particular direction: North.
Gilbert’s book is a remarkable document for its orderly discussion of heretofore unstudied phenomena. He described past views on the phenomena and criticized them, often on the basis of his own experiments. He concluded that magnetism and electricity were different phenomena and categorized materials by their magnetic and electrical properties. How did he do that? He found that heat would dissipate electrical attraction but not magnetic. This is a conclusion, then, based on controlled experimentation.
What he’s most famous for having figured out was that the Earth is a magnet, suggesting that its core was made of iron. He came up with this idea and then tested it in a variety of ways. He actually constructed spheres of lodestone and then did experiments on them with tiny magnets, determining how the angle of dip of a compass needle would vary with longitude on his test spheres, comparing that with actual compasses on the Earth at various locations. He even carved indentations into his test spheres to simulate valleys and mountains on Earth and subsequent changes to the compass needles.
Having in hand an invisible force associated with the Earth, he then anticipated Kepler and proposed that it was magnetism that was responsible for the attraction of the Earth to the Sun—he was a Copernican and because he was in England, he felt little antagonism for these beliefs. Galileo was criticized by the Inquisition for having praised the “perverse and quibbling heretic” and he himself did experiments on lodestones, with Gilbert’s work as a guide.
While Gilbert taught mathematics, he held an entirely different view of mathematics and natural philosophy. Copernicus’ book was too complicated for him and he maintained that mathematicians’ jobs were to describe the phenomena of the heavens and not to reach conclusions about physical cause. He explicitly excluded magnetism as a topic worthy of mathematical explanation and was largely silent on the subjects of motion, let alone a mathematical description of the sort that Galileo championed.
And Gilbert also worked in electricity, especially on the “amber” effect—static electricity…he knew that if one rubbed an amber rod, that it would then acquire the ability to attract paper. He invented the electroscope, which had useful scientific applications into the 20th century. Finally, it is to Gilbert that we owe the word “electricity.” A very modern physicist for his time.
As for the causes of magnetic movements, referred to in the schools of philosophers to the four elements and to prime qualities, these we leave for roaches and moths to prey upon. Gilbert, De Magnete, Book II, Chapter 3.
11.4 Magnetism
Puzzles regarding electricity and magnetism dominated the first two decades of the 19th century and it was in resolving this exciting confusion that led us to radio, TV, cell phones, and all that’s good about life. The notion that one’s hair might stand on end when combed, or that certain stones might move one another without touching had been disconcerting for millennia. Indeed, by about 1600, magnetism especially was thought to be magic and associated with illnesses and odd cures. But this period marked the beginning of thoughtful reasoning and experimentation in the natural sciences and we saw that William Gilbert literally “wrote the book” on magnetism, both describing his own researches and specifically debunking one-by-one the various ways in which magnets were thought to be helpful or harmful.
11.4.1 Magnets
Let’s review the simple facts about magnets that we’ve all known since childhood. Magnets come in one “package” a bar of typically iron in which the two ends are special: one is by convention called “North” and the other “South,” inheriting their names from a compass’s use as a pointer to the north geographic pole. The pole of the magnet that points to the north geographic pole is dubbed “North.” The other fact that we all know is that you can cut a magnet into pieces all day long and you’ll never isolate a separate north or south magnetic “monopole.” “Never” is a tough word to use in science and even though an atomic explanation for magnetism in bulk is now accepted, there are theories of cosmology which require the creation of separate, magnetic “charges” that have yet to be discovered.

Figure 11.5: This is familiar to you since you were a child.
If you come near to a target north pole with a second magnet’s north pole, the target will be forced away. Likewise, if you approach with the opposite, south pole, the magnets will be attracted. Endless fun. But what’s actually going on and how to characterize the phenomenon? Clearly there are forces created between magnetic poles with no material connection between them and this had been a puzzle since the Greeks created the first refrigerator communication device. (Okay. I made that up, but the Greeks first noted magnetism and named it for one of two towns called Magnesia—there is dispute about which.) In any case, the order is clear:
things everyone knows about magnets
Magnetized objects have both “north” and “south” poles which always seem to come in pairs and cannot be isolated.
Magnets exert forces on Magnets: Like poles repel and opposite poles attract.
🖥️
Please answer Question 1 for points: About a compass
11.5 Electricity: Poor Richard
There were various attempts to study both electric and magnetic forces, although the idea that there might be a connection between them had not occurred to many people, it was clear to those who came after Newton that some sort of Action at a Distance seemed to be going on. In 1747, Ben Franklin (1706-1790) took time out of his busy social life in London and Paris to experiment and set the course for our understanding of electricity. This man traversed the Atlantic Ocean eight times in his life and his wit and romantic appeal was familiar in Britain and especially France. While he came to it naturally, the Enlightenment fever which by that time had overtaken Paris certainly influenced both Franklin’s politics of individualism and self-determination, and his innate inquisitiveness to try to understand the “how’s” of the natural world. We all know him in scientific lore for a foolhardy experiment in the rain. But he studied many things and it was for electricity where he had his most significant impact in physics.
Franklin’s electrical experiments began in 1747 with a glass rod and silk cloth, and after sufficient experimentation he was inspired enough to write a book of his numerous experiments in electricity four years later. It was here that he guessed that lightning was a manifestation of electricity, and he proposed a method to prove it. While not necessarily due entirely to Franklin, by the time he was done with his scientific work it was generally acknowledged that:
Things everyone knows about electric charges
Electrical Charges exert forces on electrical charges: like charges repel and opposite charges attract. Electrical charges can be isolated from one another.
🖥️
Please answer Question 2 for points: Franklin’s model
11.5.1 Franklin: When Your Tool is a Hammer…
…then everything is a nail. Isn’t that how the saying goes?
Franklin’s model for electricity held sway for nearly a century: he asserted that electricity was a single fluid, just like everyone thought heat was a fluid. Neither was a bad guess, although both were wrong, but one works with the tools that one has and the mathematics of fluid flow and thermodynamics were being developed at that time and became quite sophisticated by the middle of the 19th century. It’s interesting that while electric and magnetic fields are not fluids, the mathematics used to describe them is very similar to that of fluids. So barking up the wrong tree can sometimes still be a worthwhile experience (unless, of course, you’re an actual dog).
Franklin’s “fluid” fit into the porous volumes of all substances. If two bodies had the same amount of fluid, they were neutral. But the fluid could ooze from one to the other and a body which had an excess of the electrical fluid would repel another similarly “full” body, and attract a one who’s porous material contained less. How this fluid exerted its force was not understood and collectively people threw up their hands and attributed it to the same mysterious Action at a Distance attributed to Newton’s Gravitational Law. And like for gravity, the force was instantly felt across otherwise empty space.
Because of this to and fro flowing, Franklin was led to postulate a conservation law, that the total amount of electricity was conserved and only just moved from one place to another. This imaginative and in pictorial process describes one of the most important principles in Particle Physics: that electrical charge is conserved. Remember our definition of Conserved Quantities?
Net Electrical Charge is Conserved.
Just like our discussion of the conservation of energy and momentum, this conservation law is related to a symmetry, but a complicated quantum mechanical symmetry for which there is no classical description. It is one of the most fundamental laws of Nature.
This movement of charge he called a current, the word we use today, in homage to that fluid-inspiration. Of course, we also speak of current flowing from one terminal to another, which in turn implies a direction for current. From Franklin we also get the language of “positive” and “negative” charges. He thought that the body which had been relieved of its fluid was then “negative” and that the fluid itself was an addition, hence “positive” in a body in which it’s accumulated. Of course, today we understand that “flow” in circuits is the nearly free transport of electrons within a copper matrix, which only loosely binds them to a particular nucleus. Today we describe the flow in Franklin’s terms, from positive to negative, but the more dominant actual charge motion is from the negative terminal to the positive.
Moving electrical charges are an electric current.
Currents
Usually, we think of a current as negative electrons flowing in a copper wire. While they are confined to the wire any movement of electric charges is a current. One could have a current of electrons without wires…like a lightening bolt…or positive protons in a partile accelerator beam. Both are currents and if the same number of electrons or protons flow, then the magnitude of the currents would be the same.
Franklin named things and electrical matters were no exception, “I feel a Want of Terms here and doubt much whether I shall be able to make this intelligible.” He was inventing a science. In addition to his terms “positive” and “negative,” we use “plus” and “minus” and the symbols \(+\) and \(-\) and the words “charge” and “battery.”
🖥️
Please answer Question 3 for points: Conserving charges at the LHC

Figure 11.6: Fiction from Courier and Ives.
The Kite
So did Franklin actually fly that kite? Probably not the way the legend holds, certainly not as the Currier and Ives etching in the figure suggests.
First, it had already been done, so he wasn’t first. And second, he would have died had he done this in an actual lightning storm, as happened to Georg Wilhelm Richmann in St. Petersburg in 1753. No, what Franklin probably did in his demonstration in Philadelphia in 1752 was fly a kite high enough to collect some charge along the wet kite string from a storm cloud and then suggest that lightening’s current was from the same source. And then he surely waddled for cover.
11.5.2 Science Follows Technology
Franklin’s research and that of others who quickly followed was due to their imaginations, but also to some major technological inventions. One of the first was the improvement of the electroscope as shown here.
Using a nearly evacuated bell jar and thin gold-leaf tabs, small amounts of charge could be deposited and relative amounts determined by the separation of the leaves. This was the primary device for measuring electrical charge throughout the 18th and 19th centuries. But it’s hard to generate measurable amounts of electric charges when all you’ve got is muscle-power, glass rods, and silk. Furthermore, it’s delicate work since it’s hard to keep charges isolated as they will quickly bleed away into even slightly humid air.
This situation was made much easier when in 1745 at the University of Leyden, a glass jar was surrounded by a metal can with another metal can on the inside: a cylindrical, metal-glass-metal sandwich as shown here in the figure.
It was found that this “Leyden jar” could be “charged” by successively adding increments of charge, which would stay on the cans and grow to even dangerous amounts. Today we call such an arrangement a “capacitor,” after the fact that a capacity of charge can be stored on it. The Leyden Jar made it possible for researchers to store and then use charges in their investigations without having to create them over and over. Franklin was “filling” a Leyden jar in his kite experiment (which you can see beside his foot in the figure above in the thunderstorm). But charge still needed to be created by frictional means—either by rubbing two materials together by hand, or by more efficient Wimshurst devices, large circular plates with brushes which could be turned by hand as in this “Wimshurst Machine.”
11.5.3 Eel Be Sorry
One of the most important devices is derived from a fish story. Well. Not exactly a fish. Eels were imported to Europe from South America and Africa as a delicacy in the mid-1700s, and their strange talent of generating enough voltage to charge a Leyden jar made for endless fascination in 18th century Europe. In 1786, the physician Luigi Galvani (1737-1798) was dining in a Bologna restaurant as a thunderstorm was approaching and he noticed that frogs legs hanging near a iron railing were involuntarily twitching. He drew the conclusion that this was the same effect as that of the eel, and studied it.
The biological effects of this “Galvanism” were ghoulishly investigated him and others by discharging Leyden jars in the bodies of guillotined prisoners and their severed limbs. You can only imagine how startling it must have been to see the dead move and public demonstrations made the phenomenon a popular topic. (This “cutting edge” research is known as one of the inspirations for Mary Shelley’s creation of Frankenstein.) Another Italian, Galvani’s friend Alessandro Volta, noticed that two dissimilar metals in salt water would produce the eel’s effect inorganically and in 1800 Volta constructed a sandwich of copper and iron/zinc disks, separated by cloth soaked in salt solution. This “Voltaic Pile” is shown on the right.
This was the forerunner of the battery which made it possible for natural scientists to create large amounts of charge, which they could store in their Leyden Jars and to further study their motion—currents.
11.6 Forces from Electricity: Coulomb’s Law
Amounts of charge were very difficult to determine and of course their actual nature was unknown. Charles Coulomb was a French mathematician-military engineer who was exceedingly proficient with instruments and in 1784 succeeded in building a very delicate “torsional balance” of precisely machined metal balls. These he would attach across a lightweight beam, which in turn was suspended at its center by a thin wire. Gently pushing the balls in a plane around the center of the brace would twist the vertical wire and that twist could be precisely measured and converted into the force of the push. By charging the suspended balls and separatley, the fixed, external balls to create a push (or pull), Coulomb was able to determine the amount of force exerted by given amounts of charge, and the degree to which this force changed when the charges were separated.
🖋 📓
Rather surprisingly, he found this force has a familiar form:
\[ \begin{equation} F(e) = k_E \frac{Q_1 Q_2}{R^2} \tag{11.1} \end{equation} \]
\(Q\) or \(q\)
The letter \(Q\) is used for electrical charge. I’ll sometimes use \(Q\) or \(q\) to refer to the charge of a sub-atomic particle, when it matters.
which today we call Coulomb’s Law, the force between two charge collections \(Q_1\) and \(Q_2\), which are separated by a distance, \(R\) as shown in the figure. The value of the constant in front, \(k_E\), depends on the units employed. Using “Coulombs” as the unit for charge, along with meters for the distance, \(k_E\) can be determined in MKS units to be:
\[k_E=9 \times 10^9 \text{ Nm}^2/\text{C}^2 \nonumber\]
which is called Coulomb’s Constant.
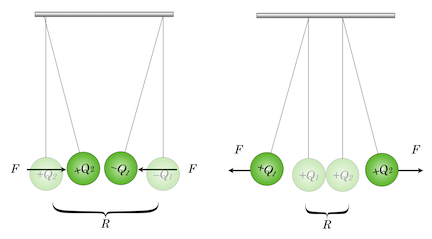
Figure 11.11: On the left, two charged insulating balls with opposite charges attract and on the right, with same-sign charges, repel.
Notice that Eq.(11.1)suggests that the electrical force depends directly on the magnitudes of the charges and the inverse square of the distance that charges are separated. The constant of proportionality, \(k_E\), is arbitrary until the units of charge and distance are specified. Notice that the sign of the charges matters here. Maintaining Franklin’s designation of plus and minus, if we make one of the charges plus and the other minus, then the force in the equation is algebraically negative. So, this means we have to be very careful about what force is on “whom.” Here’s how to think of it: If we draw an arrow from charge \(Q_1\) to \(Q_2\), then Equation (11.1) represents the force on \(Q_1\) due to \(Q_2\) and if the charges are opposite in sign, then they are attracted to one another and the negative sign in the force equation is just telling you that the force is in the opposite direction of the arrow you just drew. The unit for charge that’s commonly used is the Coulomb.
A Coulomb of charge is an ENORMOUS amount of charge. For example, a lightening bolt will consist of only 10’s of Coulombs.
Wait. Then WHY use it?
Glad you asked. The definition of a Coulomb is historical (hysterical?) and has almost no bearing on real-life. But we’re stuck with it. A couple of examples will make this clear.
🖋 📓
Please study Example 1: What is the force between two charges of 1 Coulomb?
Are you kidding me? This force is 2 billion (with a B) pounds. If this were the weight of some object, it would have a mass of \(W/g = 9 \times 10^9/9.8 = 918\) billion kg. That’s the weight of 10 Nimitz-class super-aircraft carriers—the attraction of the Earth to 10 aircraft carriers stacked one on top of the other.
Just let that sink in…with the emphasis on “sink.” Let’s make it worse. How many Coulombs is the charge of an elementary particle?
🖥️
Please answer Question 4 for points: Charge on your comb
🖥️
Please answer Question 5 for points: Force between a proton and an electron
🖥️
Please answer Question 6 for points: Forces in a nucleus
🖥️
Please answer Question 7 for points: Accelerations of charges
11.7 Forces from Currents: Electromagnetism
There was a lot of patient electrical experimentation during the early 1800s. And, as sometimes happens, the historic breakthrough came by accident. Accounts differ, but those of us who lecture for a living like to think that the following version is true! As the story goes, the Danish natural scientist Hans Christian Oersted was giving a public lecture in 1819 about the heat given off by electrical currents when he made a discovery.
(Wires get hot, as you know from playing with batteries.) He generated his currents using a Volta’s Pile and for some reason had a compass on his lecture bench which was pointing to the North as compasses will do. His current-carrying wire was above it, along the North-South direction as well.
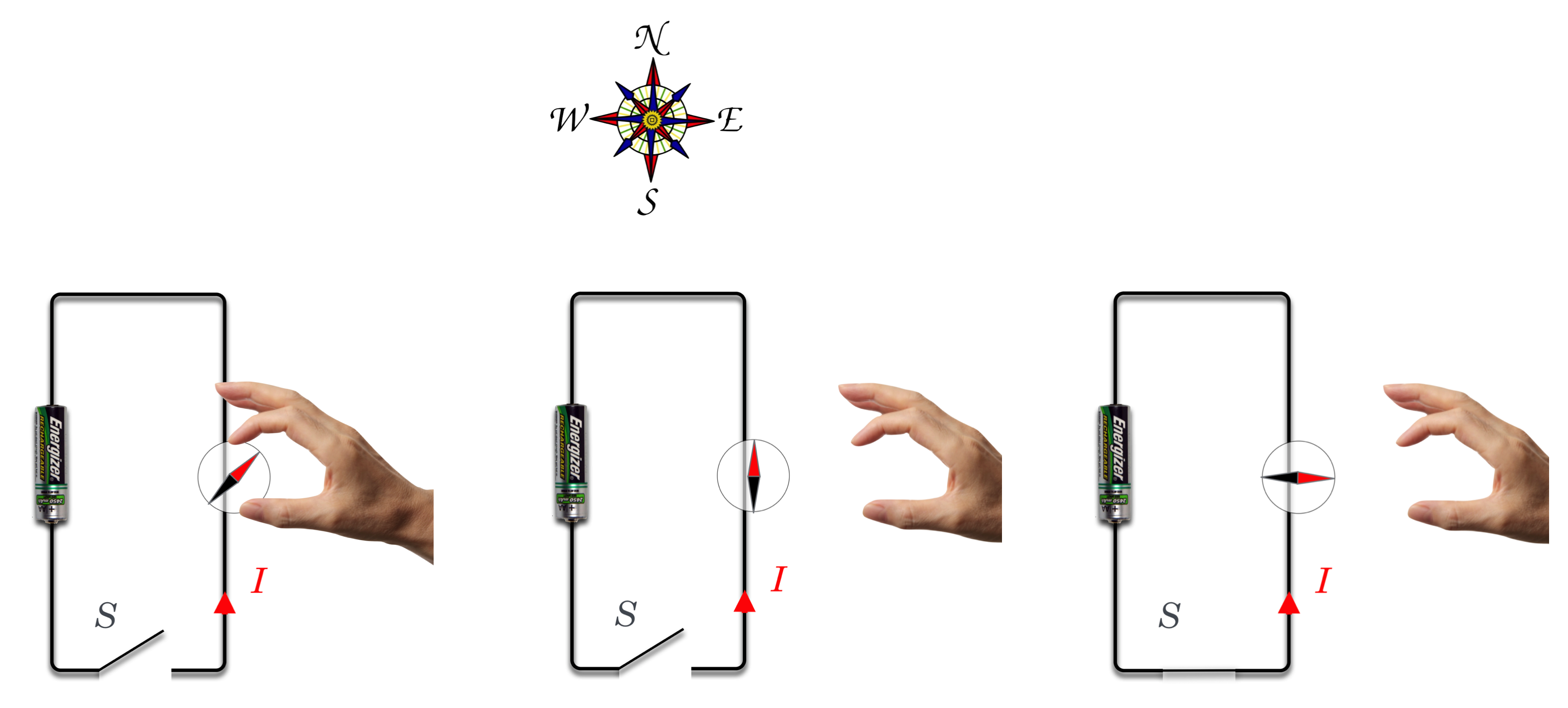
Figure 11.13: Shown is a circuit with a switch (S) and a battery with the positive pole down. When the switch would be closed, current would flow counterclockwise. In (a) a disembodied hand brings a compass near to the wire. In (b) the compass recognizes that magnetic North is to the top of the figure and it points that way…as is the job of a compass. Then in (c) S is closed and current flows as shown and Oersted’s discovery was that the compass “forgets” all about the puny Earth’s magnetic field and responds to the current.
When he turned on his current, the compass needle jumped and pointed to the West! With nothing up his sleeve, he had demonstrated a brand new connection between currents (charge) and magnetism:
Currents exert a force on Magnets perpendicular to the current.
I don’t know how composed Oersted remained during the demonstration, because this would have been quite a shock (no pun intended!). He finished his lecture and then went into feverish experiment-mode, studying the effect during the ensuing weeks. He found a number of surprising results. For example, the compass was not attracted to the wire. Newton’s gravitational attraction would have led one to expect that two objects which are the source of a force should be attracted directly towards one another—like the gravitational force. No, the compass needle did something unusual: it twisted.
Oersted interpreted this as a magnetic influence of the same nature as that of the earth (after all, it’s a compass) that was radiating outward from the wire. Here, he was wrong and a more careful examination of the effect – which is hard, because the force is very weak even for very large currents – shows that the magnetic influence is not radial, but circular, around the wire as shown in this sketch.
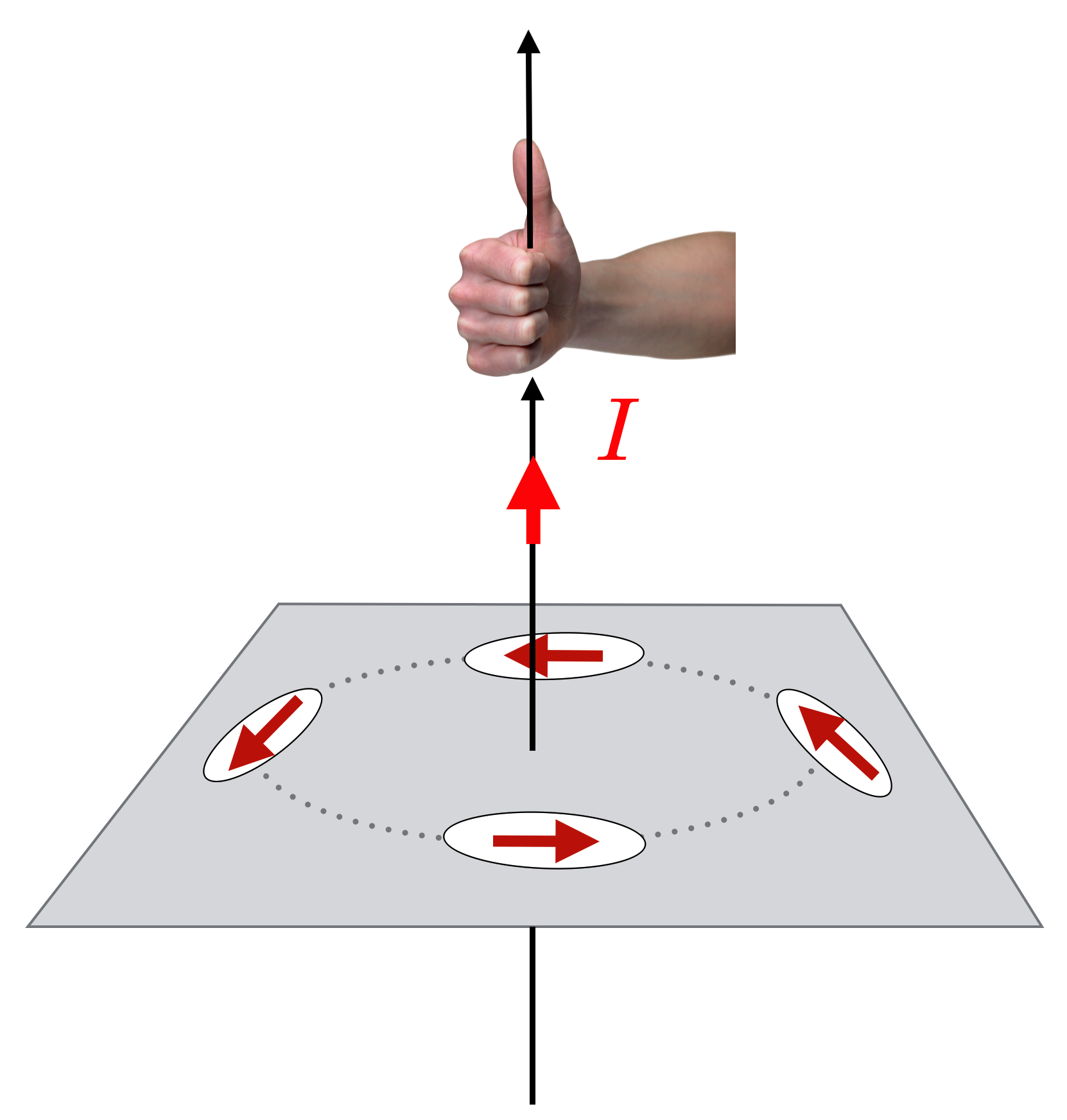
Figure 11.14: Oersted’s very careful experimentation demonstrated that a compass needle responds in a circular pattern around a wire carrying current. The direction of the north pole of the compass nee- dle can be found by using one of many “Right Hand Rules.” Here if your thumb points in the direction of the current, then your fingers curl around the wire and point in the direction of the north pole of the compass, which is shown by the red arrows. We’ll reinterpret this in terms of the Magnetic Field in the next chapter.
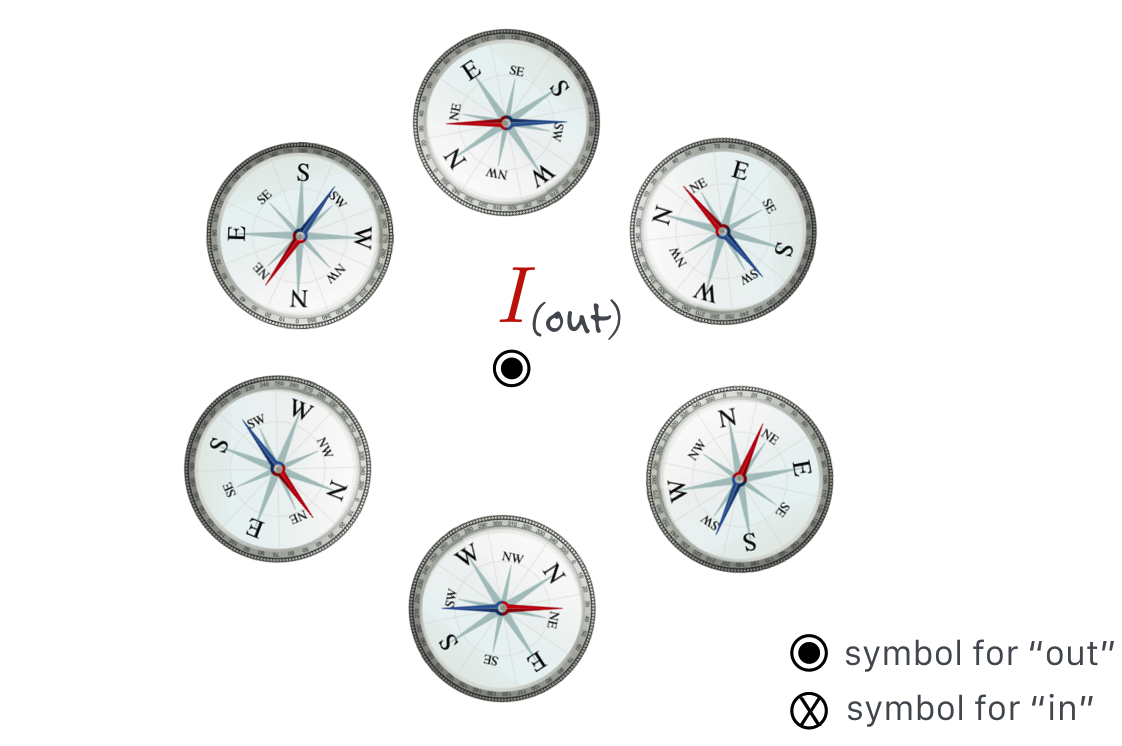
Figure 11.15: The above figure reconfigured to look down at the current coming out of the screen.
When the current flows, it’s there. Turn off the current, it disappears. Reverse the direction of the current, and the other pole of the compass is attracted. There is a rule-of-thumb (again, no pun intended!) on how to identify the direction of the magnetic influence from a wire by using your right hand: the first of a handful (sorry! no pun again!) of “Right Hand Rules”: With your right thumb in the direction of a current, your fingers will curl in the direction of the magnetic influence.
🖋 📓
Please study Example 2: More finger-pointing…can you predict the compass needle direction?
Oersted wrote about this effect and went on tour, demonstrating it around Europe and causing an enormous stir among natural scientists. That there was a connection between electricity and magnetism was now undeniable and this led to a number of speculations about how and under what conditions these connections might hold. The idea came more naturally to Oersted than to others because he had a particular religious belief, “Naturphilosophie,” that held that all of Nature is connected and so he was open to unification of all natural phenomena. Since the traditional way to make magnets move is with another magnet, it was apparent that what Oersted had done is demonstrate that:
Currents create a magnetic force, in a circular pattern around the current.
🖥️
Please answer Question 8 for points: Currents and compasses
Oersted’s phenomenon was demonstrated at the Académie des Sciences in Paris on September 11, 1820 and in the audience was Mariè Ampère, a troubled French mathematician. He was precocious in mathematics (and many other things)—especially calculus and the refinements of Newton’s physics. But a melancholy man, he was sad most of his life. His father had been executed during the French Revolution and although Ampère was happily married, he lost his wife in 1803 while he was away at a new teaching position. Separation from her and their young son had been especially hard, as she’d already been ill when he departed and so his guilt sent him into a gloom which stayed with him for the rest of his life. He married again, disastrously, but separated from his wife after only a year and a half with their daughter under his custody.
During the week that followed that momentous autumn lecture, Ampère managed to work out and measure Orested’s effect, but he went further. He quickly constructed a delicate, current-carrying coil which could be suspended with the axis of the coil horizontal. When current flowed and a bar magnet was brought near, the coil pivoted and was attracted to or repelled from the magnet. The coil has a left and right side, like poles—you can again use your right hand and wrap your fingers in the direction of the current and your thumb will now point in the direction of a “North” pole-like direction.
So the coil of current behaves as if it were itself a bar magnet! From this he quickly hypothesized that all magnetism is due to “molecular” current coils and that there must be circular currents in the center of the Earth to produce the Earth’s magnetic field.
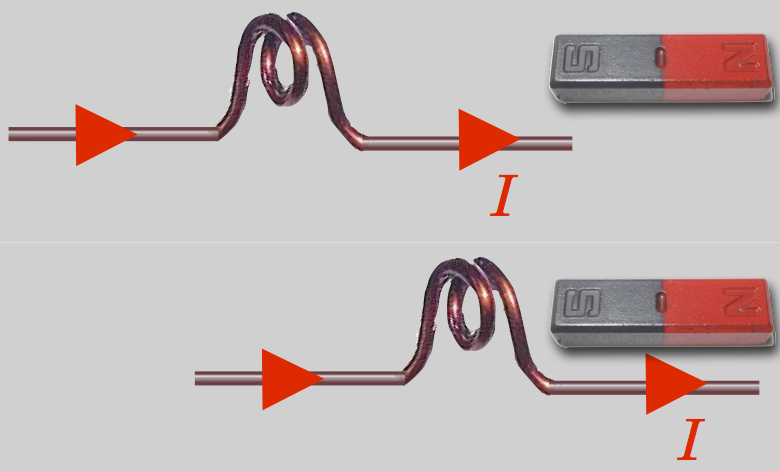
Figure 11.17: A current-carrying coil behaves like a magnet and is attracted or repelled depending on the direction of the current.
A coil of wire carrying a current behaves like a bar magnet.
Not content, he went further: he further reasoned that if currents cause magnetism, then one current ought to influence another current, just like magnets influence other magnets. By producing very high currents he showed that two parallel wires experienced a force between them—attractive when the currents are parallel and repulsive when opposite:
Currents exert a magnetic force on other parallel currents causing them to attract (if the currents are aligned) or separate (if the currents are anti-aligned) .
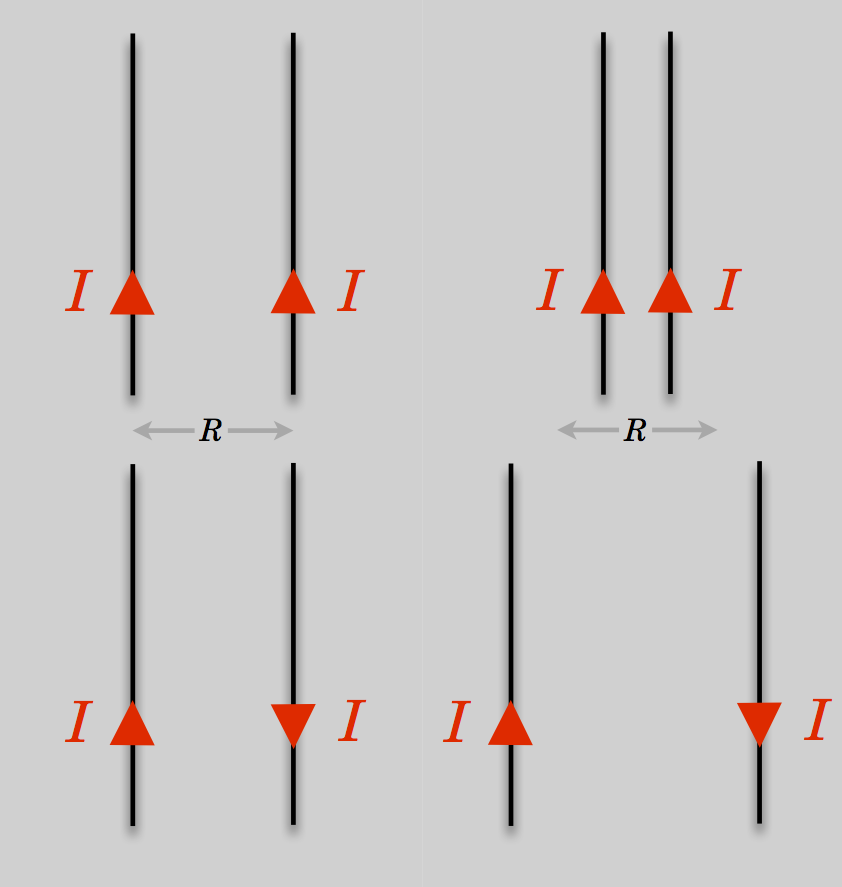
Figure 11.18: Currents in parallel wires will create an attractive force (above) when the currents are parallel and repulsive force (below) when antiparallel.
With his mathematical skills, he was able to work out the force on one wire due to another, which is related to what we call Ampère’s Law. He did this work extraordinarily fast and used a procedure that’s not generally used today. By November, he had a complete Model for magnetism: magnetism as due to the collective action of little, molecular currents. He came to this through experimentation as well as his mathematics. Ampère’s reputation was secure and he was able to create a course in “Electrodynamics” in which Ampère furthered his researches into the relationship between electricity and magnetism with both inspired mathematics and impressively precise experimentation. While his place in the history of physics was secure, his relationships with his surviving children were unpleasant. Consistent with his dark outlook, his son, a successful historian, and he were always at violent odds and his daughter was an alcoholic who lived with her husband in Ampère’s home. This was a life not made in heaven, one of constant turmoil, including frequent visits from the police.
11.8 Inverse Square “laws”
Now you’ve seen a very familiar behavior of two models in nature, Newton’s Gravitational law and Coulomb’s law. Both have the same abstract form: \[ F_{12}=\text{Constant}\frac{\text{Source}_1\text{Source}_2}{R_{12}} \] Here we’re to imagine two “sources,” named One and Two, which are separated by a distance \(R_{12}\) that experience a force, \(F_{12}\) between them. Obviously:
- Gravitational force: Source\(_i\) = \(M_i\), a mass, in units of kilograms
- Electrical force: Source\(_i\) = \(Q_i\), an electrical charge, in units of Coulombs
Some characteristic fundamental Constant sets the scale for how large such a force might be. If Newtons are our force units, then:
- Gravitational force: “Constant” = \(G=6.673×10^{-11}~\text{ Nm}^2/\text{kg}^2\)
- Electrical force: “Constant” = \(k_E=9 \times 10^9 \text{ Nm}^2/\text{C}^2 \nonumber\)
Perhaps you’re not surprised that there’s also an “inverse-squared” rule for magnetic forces? We don’t talk about it very often because it’s the force between two magnetic poles, which we don’t ever see isolated in nature.
But Mr Coulomb also studied that force with his sensitive balance by suspending a bar magnet from its center and then using the pole of a long second magnet to attract or repel the suspended one. So we then have:
- Magnetic source: Source\(_i\) = \(m_i\), a unit magnetic pole, in units of Ampere-meter
- Magnetic force: “Constant” = \(k_m=1 \times 10^{-7} \text{ N}/\text{A}^2 \nonumber\)
Okay. That’s unfortunate. Yet another use of the 19th letter off the alphabet, m. And, a current has crept into this discussion of magnets as we just learned, “Amperes” is a measure of electrical current (“amps”). So this is indeed a cumbersome item.
11.8.1 Thing One
Let me let the cat out of the bag (although in my opinion, bags are a good place to have cats…I know. Sorry.) by looking at these two constants, \(k_E\) and \(k_m\). First let me replace the unit of Ampere with its more basic unit of Coulomb/second. \[ k_m=1 \times 10^{-7} \text{ N}/\text{A}^{-2} = 1 \times 10^{-7} \text{ N}\text{C}^{-2}\text{s}^2 \nonumber \]
Let’s relate them now as a ratio: \[ \begin{align} \frac{k_E}{k_m} &= \frac{9 \times 10^9 \text{ Nm}^2/\text{C}^2}{1 \times 10^{-7} \text{ N}\text{C}^{-2}\text{s}^2} \tag{11.2} \\ &= 9\times 10^{16} \;\;\text{m}^2/\text{s}^2 \end{align} \] Can you see that this last line is the square of a velocity? If we take the square root of this: \[ \sqrt{\frac{k_E}{k_m}} = 3 \times 10^8\;\;\text{m}/\text{s} \tag{11.3} \] A particularly famous speed…that of light. So stay tuned for this as it will be a big deal in Lesson 14.
In fact, this will be the biggest deal of the 19th century and be the direct inspiration to Einstein and his Theory of Relativity.
11.8.2 Thing Two
Why is this inverse square such a thing?
Let’ suppose that you’re going to paint the inside of a beach ball by exploding a very precisely constructed ball of paint.
Wait. Why would you do that?
Glad you asked. It’s a metaphor to make a complicated mathematical calculation a simple mind-game.
You detonate your paint-bomb and droplets of paint fly out in all directions uniformly coating the inside. We could estimate the darkness of the paint covering by counting the number of little drops that uniformly stuck to the inside.
Wait. Again?
Glad you asked. Stop it.
Suppose that worked well and we want to do it to a beach ball that’s twice the size of the original, but using the same paint-bomb. Would the darkness be the same? Darker, or lighter?
Of course, it’s going to be lighter by how much? By a factor of 4 less. That’s because the area of a sphere (the area of the inside of the beach ball) is \[ A(\text{sphere}) = 4 \pi R^2 \] If you increase \(R\) by a factor of 2 then the area becomes a factor of 4 bigger. But if the paint drops uniformly coat the bigger sphere, then there are going to be 4 times fewer of them per unit area than for the half-sized beach ball.
That’s the essence of the “inverse square-law” for any of these three different models of physics. It implies something about an emanation (the “paint”) and it’s a statement totally about geometry, the fact that the area of a sphere is what it is for three space dimensions.
Suppose space had more than 3 dimensions? Up, down, in and out and…over there? Then that “2” in the denominator of each of those relationships would be something other than two. And boom. We’ve got a whole field of experimental research: trying to measure that exponent very well to check that we have 3 dimensions in space or something different.
11.9 Modern Ideas
Let’s remind ourselves of modern interpretations of these ideas—things you all know. The historical discussion above was about regular-sized objects that were electrically charged or magnetized. The idea of atoms was still highly speculative, much less electrically charged particles.
The sub-atomic objects in nature are either: positively charged, negatively charged, or neutral (zero charge). As we will soon see, the total electrical charge of any macroscopic object (your hair in winter and the comb that charged it?) can’t be just any value, but instead is a multiple of an apparently special amount.
🖥️
Please answer Question 9 for points: Forces on wires carrying currents
When electricity was first studied—Franklin’s time—there was no idea of an electron or a proton and their particular charges. Rather “stuff” was charged: everyday-sized things, the charge of which might be pretty large. The unit of charge is the “Coulomb,” (abbreviation is “C”), named for our Charles Coulomb of previous pages. He studied regular sized objects and so they had lots of charge. But when the 20th century came around and people started to study atomic-sized objects it became apparent that the most natural value of charge was not Coulombs…but nano-nano Coulombs: the fundamental electrical charge is that of single electrons and protons. It was a couple of decades into the 20th century when the value of the discrete, fundamental charge was finally measured as the charge of the proton, which in magnitude is the same as the charge of the electron. Here it is. Lot’s of zeros: Let’s look at this number. There’s a lot of information in it—beyond just its value. The first thing you notice is that it’s tiny, as I warned:
\[e = 0.0000000000000000001602176487(40)\mbox{ C}.\]
The second thing you notice is that there are lots of non-zero numbers to the right of the decimal point! That is, it’s measured to very high precision, which should suggest to you years and years of patient, careful measurements by lots of hard working people. The third thing you notice is the \((40)\) at the end of that string of numbers which are the only digits in the string of 12 that are considered to be slightly uncertain. So the precision to which this number has been measured is \(0.00000000040/1.602 176 48740 = 2.49 \times 10^{-8}\) percent! You would correctly conclude that knowing this number must be a pretty important thing. It’s precision is much higher than that of the other fundamental physical constant that we saw earlier, the Gravitational Constant, G.
Electrical charge appears as multiples of a fixed, fundamental amount called \(e\).
We use the symbol \(e\) to represent the value of this fundamental amount of charge (so we don’t have to carry around all of the decimal points!). So in this way, we would say that the electrical charge of:
- an electron is \(Q_e = -e\text{ C}\),
- a proton is \(Q_p = +e\text{ C}\), and
- a neutron is \(Q_n = 0 \text{ C}.\)
You might wonder why they are the same value? We don’t know. Franklin had a 50-50 chance of guessing which direction current flowed, and he got it wrong since the objects that move in a wire—that are an electric current—are negative electrons. So we’re stuck with his assignment.
Wait. Why is there a fundamental unit of electrical charge?
Glad you asked. We’d love to understand this and it’s an object of speculation and research. Well, guess what. Just when we thought we’d nailed down the fundamental unit of charge in Nature…quarks happened. We’ll talk a lot about these fundamental entities later, but they have the surprising property of electrical charges which are not multiples of \(e\), but rational fractions, namely \(Q_{\text{ quarks}}\pm 2/3e\) or \(\pm 1/3e\). Quarks go together to make many of the particles that we understand to be composite by adding their fractional charges to make …whole multiples of \(\pm e\). We take \(e\) as the fundamental quantity primarily out of habit and because the electron has this fundamental, whole unit.
11.9.1 Electrical Current
Earlier I noted that we define the unit of electrical current as that necessary to cause a particular force to separate two parallel currents. But most of us think in practical terms: a “current.” An electrical current is a measure of how much charge passes a given point, during a given time. It’s measured in “Amperes” as you know. Here’s what an Ampere is:
\[1\mbox{ Ampere}= 1\mbox{ Coulomb per second:}\;\;\;\; 1 \text{ A}= 1\text{ C/s}.\]
You’ve probably all played with batteries and wires in school and you know that if you set up a little circuit with an AA battery, some wire and a bulb that after some trial and error you can make it light. We say that the current flows from the positive terminal of the battery to the negative terminal, but that’s Ben’s mistake: it’s actually the electrons that move in a wire and so the current is in the opposite direction from the actual charge motion. We’ve learned to live with that and we call positive current from the positive terminal of a battery.
An electrical current is rate in time at which electrical charge moves.
🖋 📓
Please study Example 3: How many electrons are in a Coulomb of electrons?
🖥️
Please answer Question 10 for points: Coulombs in a current
That’s more interesting, but maybe distressing: There are about \(10^{28}\) electrons in an average human body so how many Coulombs of charge are there in the average human body? An easy calculation: …which is a lot. Given our aircraft carrier example, why aren’t we each crushed by our mutual electrical forces? It’s because we’re neutral. For every electron in our body—and every other element—there is a proton. All of those little \(e-p\) pairs cancel and the net result is that we don’t repel or attract one another. In fact, it appears to be a law of nature that all electrical charge comes ready-made with something of the opposite electrical charge. There aren’t positively charged people, nor trees, nor stars, nor galaxies. This is a really important observation about the universe and we’ll talk about it later.
But it does point out an important point about electrical charge: the positive and negative electrical charges add as positive and negative numbers. Like arithmetic. So if I mix two charges together, say \(Q_1 = +10\) and \(Q_2 = -5\), then the end result will be a net charge of \(+5\).
The work of Coulomb, Ampere, Volta, Oersted and many others created a body of experimental knowledge and considerable confusion about the nature of electricity. Magnetism had been perplexing for centuries and while Ampere’s guess as to its nature was close to the truth, the real explanation was more than a century out of reach in the early 1800s.
What was required was someone to look at the evidence with fresh eyes. Someone with a natural instinct for experimental technique and a modern dedication to uncovering Nature’s secrets. What was required was a young man born in the extreme poverty of newly industrializing Britain with almost no education. Michael Faraday came along just at the right time to sort it all out and to intuit the strange solution. Almost miraculously, the young James Clerk Maxwell overlapped the mature Faraday and developed the mathematical power required to complete Faraday’s insight. One of the most incredible scientific duos in history brought about the beginning of Modern Physics.
11.10 What to Remember from Lesson 11
Let’s add up all of the new things in this lesson, in a slightly different order from how I introduced them.
- Elementary particles often have electrical charges. Electrons are negative, protons are positive, and neutrons have no charge at all, they’re neutral. We would say in our shorthand: \(Q_e = -e\), \(Q_p = +e\), and \(Q_n = 0\).
- \(e\) is the fundamental unit of electric charge and has a value of \(e= 1.6 \times 10^{-19}~\)Coulombs. Coulombs are an old unit of electrical charge.
- An electric current is electrical charges in motion…usually electrons (not always) and usually in a metal wire (not always). The unit of electrical current is the Ampere and it’s a measure of the amount of charge passing a point in a given time: \(1~\)A \(=1~\)C/s.
- A current sets up a magnetic influence in a pattern of circles centered on the current: currents cause magnetism.
- Does magnetism cause currents? (Gotcha. That’s for the next lesson.)