Lesson 10 Galileo’s Astronomy and Newton’s Gravitation
Galileo’s Big Mouth and Newton Explains the Solar System
10.1 Contents
10.2 Goals of this lesson:
- I’d like you to Understand:
- How to calculate the gravitational force between two masses
- How to calculate the weight of any object on any planet
- How to calculate gravitational potential energy
- I’d like you to Appreciate:
- How Galileo’s astronomical discoveries charted new ground in astronomy
- How Galileo’s approach to science laid groundwork for the modern version
- Newton’s argument regarding the Moon and the Apple
- What being in orbit implies about “falling”
- Escape velocity
- That gravitational potential energy is negative
- I’d like you to become Familiar With:
- The later lives of Galileo and Newton
- The importance of Galileo’s Letter to the Dutchess Catherine
10.3 A Little Bit More of Galileo
When we last left Galileo, he was in Padua working out the correct understanding of falling bodies and projectiles. He didn’t publish that work until he was under house arrest in his villa outside of Florence and had to smuggle it out of Italy to the Netherlands. How his arrest-story came about is legendary, and not necessarily how most people imagine it. First, some more science, then some of the back-story to his troubles with the Inquisition.
Galileo had been in Padua for 16 years when in May of 1609 he heard of a novelty that was being sold in France, Germany, England, and the Netherlands where it was invented. This was of course the telescope. He was good with with his hands and eventually employed an instrument maker. Together, within a month, from only a word of mouth description, he was able to grind and polish lenses and construct his own telescope. It was just 3x magnification, not as good as what was “out there.” But he improved on his technique and built 8x, 15x, and 30x versions. Here is one of his first prototypes from the science museum in Florence, Italy. He used it to look across the land and water and then…he looked up.

Figure 10.2: One of Galileo’s original telescopes from the wonderful Museo Galileo in Florence, Italy.
In August of 1609 he took his then 8x version to Venice and demonstrated it to the intellectual community, and also politicians. Galileo always had his family’s debts on his mind and he gave an exhibition from the top of the St. Marco tower and showed that one could see ships much further away than with the naked eye. Venice, was a maritime power and sometimes the target of naval attack from the East and so the Venetian Senate had a vested interest in this new early warning system. They were impressed, doubled his salary, and awarded him lifetime tenure at the university…but also froze his salary at the new level. Although he was now one of the most highly paid professors in the Venetian Republic, the prohibition of any raises for the rest of his life didn’t sit well with the ambitious 45 year old.
10.4 What Galileo Saw!
Through the next year Galileo observed things that nobody had previously imagined. In November and December of 1609 he carefully studied the Moon and with his excellent artistic abilities, drew detailed images showing the mountains and craters. This was revolutionary because the Aristotelian model required the celestial bodies to be perfectly unblemished spheres. By carefully mapping the shadows of the Moon, Galileo estimated the height of crater edges and found them to be Earth-like in size. Then a month later he studied Jupiter and found what looked like three bright stars, all in a line. He continued looking in successive nights and saw a fourth “star” peek out from behind the planet and found all four of them to be moving together! Subsequent observations convinced him that they were bound to Jupiter, and not stars at all: Jupiter has moons which today we call the Galilean moons. Opportunistically he named them the Medicean moons and realized that this Jupiter-moons system was Copernican-like. Finally, when he looked into deep space the stars multiplied. He found hundreds of stars that nobody had ever seen before.
In 1611 he published Sidereus Nuncius, or Starry Messenger, reporting these and other revolutionary observations and interpretations. This figure shows the elaborately constructed title page

Figure 10.3: The title page of Sidereus from a copy in the University of Oklahoma science library. One of the most respected science libraries in the world. The translation is from a 19th century. Notice that Galileo signed this copy.
and here are a few pages from the text.

Figure 10.4: Three of the many sketches in Sidereus Nuncius. The Moon picture is famous and meticulous. The middle drawing is one of many documenting the motion of Jupiter’s four moons orbiting the planet. The right figure is his sketch of the Pleiades constellation with its seven (‘seven sisters’) stars and then all of the new ones visible through his telescope.
The Moon has a rough surface with mountains and valleys. Other planets in our solar system have moons that move according to Kepler’s laws.
When he was at Pisa, he had become friendly with the Medici family, especially the the Grand Duchess Christina. A few summers while he was in Pisa he was brought back by her to Florence in order to tutor her young son, the young Cosimo d’Medici. His bold naming of the moons after his former student – by then the reigning Duke of Tuscany – and his dedication of Sidereus Nuncius to him was an obvious ploy to again improve his circumstances and to get a new job without teaching responsibilities. He was not above groveling before royalty when he needed to:
“…scarcely have the immortal graces of your soul begun to shine forth on Earth than bright stars offer themselves in the heavens, which, like tongues [longer lived than poets] will speak of and celebrate your most excellent virtues for all time.” A tad syrupy perhaps?
The figure above shows his sketches of multiple nights’ viewing of the Medician moons. What he had found was a miniature Copernican system within the bounds of our own solar system. In fact, Kepler’s Third law would hold, but for Jupiter there would be a different proportionality constant, say \(k_J\).
Further, Siderius described his discovery that Venus had phases like the Moon which explained why it appeared to change brightness periodically, just as Copernicus had predicted. And finally, the number of stars visible with the telescope dwarfed what everyone believed was the full compliment of stars that had been carefully tallied by the Babylonians, Greeks, and Tycho. The universe appeared to be a much more interesting place than anyone had imagined.
The effect of all of this news electrified Europe and overnight, Galileo became famous, and remained so for the rest of his life. The good news? He got the job back in Florence. And the bad news: Florence was within the sphere of influence of Rome and the Pope. In fact, there had been a number of Medici popes in the family. Venice was much more liberal and was often at odds with the Vatican over one or another issue. (Pope Clement V excommunicated the entire population of Venice in 1309! Interdicts – forbidding any ecclesiastical functions were instituted against Venice in 1202, 1284, 1480, 1509, and again in 1609.) Galileo’s…unusual views…were safe in Venice, but dangerous in Florence.
He negotiated the position that not only paid well, but also importantly, raised his stature: he was The Chief Mathematician of the University of Pisa and Philosopher and Mathematician to the Grand Duke. The last title was important, for it was Philosophers who ruled the academic roost and mathematicians were the least respected. Galileo insisted on this dual, contradictory title. He took multiple victory laps in Rome where he was celebrated by the College of Jesuits and where the then Cardinal Barberini took great pleasure in Galileo’s friendship. The 47 year old was riding high.
Other planets in our solar system have moons that according to Kepler’s model.
In years to come, Galileo studied many things and wrote books on Sunspots (He learned to train his telescope on the Sun, but a student taught him to project the image onto a piece of paper so that he would not damage his eyes. The result was another kind of blemish in a heretofore perfect celestial sphere: sunspots.) and buoyancy. Here he began to get himself in trouble as a respected Jesuit competitor disagreed with him on the origin of sunspots (were they just another set of planets?) and buoyancy…what caused things to float. In both cases, Galileo was over the top and ad hominem in his nasty criticisms of his scientific adversaries. This cost him support among some of his Jesuit colleagues.
The Sun has blemishes on its surface that change in time.
10.4.1 The Most Famous Letter in the History of Science
In 1614 Galileo was denounced by name from the pulpit of Santa Maria Novella – in Florence – by a conservative Dominican priest. He had begun to be suspected of heresy – was formally denounced to the Inquisition in 1615 – and there was a growing unhappiness with him within the most doctrinaire of the Church’s hierarchy. He reacted in what was to become the Galileo-way: a strong defense is always a strong offense.
In 1615 Galileo circulated a long, open letter to the Grand Duchess Christina purporting to explain a debate at a meal that he was not at, but where his views were the topic of discussion. It’s worth quoting in length, for it forms the rallying cry of the new approach of Natural Philosophy as it morphs into a real scientific attitude (emphasis mine):

Figure 10.6: Title page of the Letter to the Grand Dutchess. Galileo wrote it informally in 1616 which was passed around. It was eventually printed in Latin in 1636, three years after he was incarcerated.
“Some years ago as Your Serene Highness well knows, I discovered in the heavens many things that had not been seen before our own age. The novelty of these things, as well as some consequences which followed from them in contradiction to the physical notions commonly held among academic philosophers, stirred up against me no small number of professors–as if I had placed these things in the sky with my own hands in order to upset nature and overturn the sciences…”
“Showing a greater fondness for their own opinions than for truth, they sought to deny and disprove the new things which, if they had cared to look for themselves, their own senses would have demonstrated to them. To this end they hurled various charges and published numerous writings filled with vain arguments, and they made the grave mistake of sprinkling these with passages taken from places in the Bible which they had failed to understand properly.”
He’s just getting warmed up:
“Again, to command that the very professors of astronomy that they must not see what they see and must not understand what they know, and that in searching they must find the opposite of what they actually encounter is beyond any possibility of accomplishment.”
And the punch-line:
“Now, if truly demonstrated physical conclusions need not be subordinated to biblical passages, but the latter must rather be shown not to interfere with the former, then before a physical proposition is condemned it must be shown to be not rigorously demonstrated… and this is to be done not by those who hold the proposition to be true, but by those who judge it to be false.”
Finally:
“Inasmuch as the Bible calls for an interpretation differing from the immediate sense of the words, it seems to me that as an authority in mathematical controversy it has very little standing… I believe that natural processes which we perceive by careful observation or deduce by cogent demonstration cannot be refuted by passages from the Bible….The primary purpose of the Holy Writ is to worship God and save souls…”
The nub of the argument was:
“They know that as to the arrangement of the parts of the universe, I hold the Sun to be situated motionless in the center of the revolution of the celestial orbs while the Earth rotates on its axis and revolves about the Sun. They know also that I support this position not only by refuting the arguments of Ptolemy and Aristotle, but by producing many counter-arguments; in particular, some which relate to physical effects whose causes can perhaps be assigned in no other way.”
<His war with theology has begun. He’s saying: the Bible does not determine what is the case in the physical world. What’s observed does. In order to overturn a fact in the world, only another observation can condemn it, not scripture. His critics accused him of re-interpreting the Bible, which smacked of protestantism and was against Church law according to the defensive Council of Trent.
Only measurements can challenge observations about the physical world. Not a religious authority or text.
Galileo had become a Copernican and there’s some evidence that this evolution in his belief happened early, but it was first enunciated in a letter to Kepler in 1597 (“….Like you, I accepted the Copernican position several years ago”) but the letter to Catherine was his coming-out.
“All our Fathers of the devout Convent of St. Mark feel that the letter contains many statements which seem presumptuous or suspect, as when it states that the words of Holy Scripture do not mean what they say; that in discussions about natural phenomena the authority of Scripture should rank last... [the followers of Galileo] were taking it upon themselves to expound the Holy Scripture according to their private lights and in a manner different from the common interpretation of the Fathers of the Church...” Letter to a member of the Inquisition.
A council of advisors was established by Pope Paul V to review the theological aspects of Copernicanism. They reached conclusion on two issues: Does the Sun sit immobile? Does the Earth move?
On the first, they concluded that to hold that the Sun was immobile and at the center of the solar system: “…foolish and absurd in philosophy, and formally heretical since it explicitly contradicts in many places the sense of Holy Scripture.”
On the second, that the Earth moves: “…receives the same judgment in philosophy and… in regard to theological truth it is at least erroneous in faith.”
This led to a banning of Copernicus’ book until corrections were made. The figure below is a page of Revolutiononibus showing some of the Inquisitor’s corrections.

Figure 10.8: At the end of the paragraph, Copernicus wrote: ‘Tanta nimirum est divina haec Opt. Max. Fabrica.’ (‘So vast, without any question, is the divine handiwork of the most excellent Almighty.’) That was to be eliminated. The beginning of the next chapter entitled, ‘De hypothesi triplicis motus telluris eiusque demonstratione’ (‘On the explication of the three-fold Motion of the Earth’) was too much for the Inquisition and they suggested instead, ‘On the Hypothesis of the Three-fold Motion of the Earth and its Explication’ which is written in above by hand.
The consequences were not terribly significant. The Pope’s advisors reported to him on February 24, 1616 and Paul asked the respected Robert Cardinal Bellarmine (who had previously defended Galileo’s letter to the Grand Dutches to the Pope) to advise Galileo to not claim that Copernicanism as fact. This was in a written document signed by both that hypothetical discussions were okay. Galileo said, “okay.” He had a nice meeting with the Pope and went home. Some years later a letter surfaced that suggested that Galileo had been admonished to not speak of Copernicanism even in hypothetical terms, but there’s ample reason to suspect that this letter was fraudulent and created in order to create a legal case to silence or imprison Galileo.
It wasn’t necessary. Galileo was perfectly capable of creating his own problems, all by himself.
10.4.2 Unforced Errors
Paul died in fall of 1616 and was replaced by Cardinal Scipione Caffarelli-Borghese as Pope Greggory XV, who then was succeeded in 1623 by Maffeo Barberini who became Pope Urban VIII. This was good, thought Galileo. Urban was a personal friend! Barbarini had supported him with poems and a stipend…even supporting Galileo’s son.
Sixteen years after his meeting with Bellarmine and Paul XV, Galileo finally went to print with his definitive publication on Cosmology, Dialogue Concerning the Two Chief World Systems. He chose to write it as a “dialog” among three people: Salviati (an actual friend of Galileo’s) is the enlightened modern thinker who defends Copernicanism, Sagredo (an actual friend of Galileo) is an intelligent layperson who’s slowly convinced by Salviati, and Simplicio is an Aristotelian, whose name says it all. The figure below is the cover of Dialogo.

Figure 10.9: The cover shows from the right, Salviati (actually, Copernicus - notice the model he’s holding), who looks more like Galileo (in the next editions a more Copernicus-looking young person is depicted), Sagredo (actually, Ptolemy, hence the turban), and Simplicio (actually, Aristotle).
For some reason, Galileo puts Urban’s own words to him in the mouth of Simplicio and that was his undoing.
Within two months, the Dialogue was removed from all shops (it was in Italian, so laypeople could read it). On the first of October in 1632 the Inquisitor of Florence appeared at Galileo’s house with instructions that he was to appear in Rome within a month. That was attention-getting. It was only three decades ago that the friar Giordono Bruno was burned at the stake for expressing heretical views about Copernicanism. Bruno had to account for much, much more philosophy and blasphemy in his short, fiery career. In fact, Bruno was the top choice for the Padua position but was arrested and executed before he could take up his post. Galileo was the second choice. So he was intimately familiar with what the Inquisition could do.
He protested illness – and indeed he was sick all the time – but Urban demanded that he travel, sick or not. He’d thoroughly lost his friend, the pope. So after 23 days of painful travel he arrived and stayed in the Florentine embassy until he was arrested and taken into custody by the Roman Inquisition. The ambassador later wrote that, “…for two nights continuous…[Galileo] cried and moaned in sciatic pain; and his advancing age and sorrow.” It was only going to get worse.
10.5 The Apple Moment: Newton’s Gravity
Suppose you could go to a mountain and shoot a cannonball horizontally, like Galileo’s table-top. If you were to increase the charge so that the cannonball is given more and more horizontal velocity…it would go further and further and eventually – it misses the ground. The figure below is from the Principia is perhaps the most fanciful thing that Newton ever depicted. He surmised that if given enough velocity the cannonball would continue to “fall” around and around: it would go into orbit. This is a part of the famous idea that transformed physics forever. Yes, the Apple.
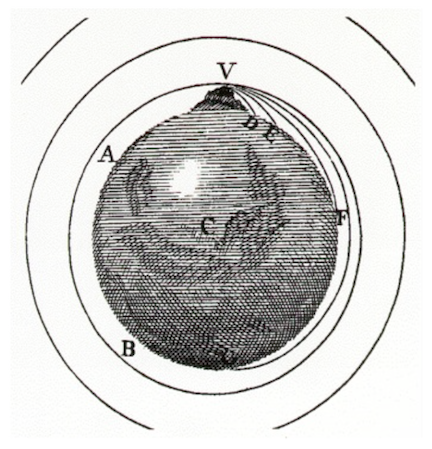
Figure 10.10: Newton’s depiction of launching a cannonball into orbit.
the apple changed everything
What I’m about to describe arguably changed not only natural science, but was the catalyst for the idea that not only science, but reason was the path to knowledge and progress. Everything we know today as how to think, how to govern, and the role of rationality in deciphering how the world works arguably stems from the “Age of Reason” the Enlightenment born in the optimism of the Newtonian synthesis.
There’s no way to overstate the importance of Newton’s Gravitational law. It made precise predictions about a number of physical phenomena, which were tested and shown to be confirmed. The very idea that a model of the universe would be quantitative and that predictions would be worth testing was itself a new idea.
Before Newton there was superstition. After Newton, there was science. Gravitation was the reason. The Aristotelian view disappeared. Ptolemey’s model disappeared. The solar system and the Sun’s rightful place was established, not to be unseated again.
There was the complication of Tycho’s model (remind yourself in Lesson 9) of the solar system which held the Earth stood still and the Sun revolved around it and the other planets revolved around the Sun. It’s geometrically the same as the Copernican model with the assumption that the Earth stands still. The stellar aberration observations necessary to show that the Earth really does move and that Tycho’s model was not correct waited until the early 1800’s when telescopes were finally precise enough.
During the 17th century the rules governing celestial objects were supposed to be different from those on Earth. Copernicus didn’t question this. Kepler hinted at a common set of rules. Galileo didn’t go there. And Newton was taught a full dose of Aristotle at Cambridge (which students rebelled against by secretly reading Descartes). But somehow he – unlike anyone before him – imagined that there was only one set of rules that governed Earth-bound and celestial objects. And he, first among all, figured out how to make a model and test it.
When he was at the farm during the plague he had a number of remarkable ideas, among which one presumably came from the apple story. There was (and still is) an apple tree at his childhood home and he surely watched many lose their grip and fall to the ground. There is one account of this famous story from his first biographer, William Stukeley describing a dinner he and the great (now old) man enjoyed in 1726:
“After dinner, the weather being warm, we went into the garden & drank tea under the shade of some apple tree; only he and myself…Amid other discourse, he told me, he was just in the same situation, as when formerly the notion of gravitation came into his mind. Why should that apple always descend perpendicularly to the ground, thought he to himself; occasioned by the fall of an apple, as he sat in contemplative mood.
Why should it not go sideways, or upwards? But constantly to the Earth’s centre? Assuredly the reason is, that the Earth draws it. There must be a drawing power in matter. And the sum of the drawing power in the matter of the Earth must be in the Earth’s centre, not in any side of the Earth.
Therefore does this apple fall perpendicularly or towards the centre? If matter thus draws matter; it must be proportion of its quantity. Therefore the apple draws the Earth, as well as the Earth draws the apple.”
There it is. That’s the story. Further, if the Earth has “drawing power,” maybe whatever it is about the Earth that draws an apple to the ground might also pull on the Moon. How much? Galileo thought that the force of the Earth on objects would be constant everywhere, but Newton guessed that it was not…that it should be diluted as one moves away from the Earth. He guessed (and later showed mathematically) that it could be presumed to be the center of the Earth.
He had to assume that the Moon moves in a (near) circle around the Earth. And he had to presume that the same rules governing objects moving in a circle on the Earth would hold for the Moon. He (privately in 1666) and Huygens (publicly in 1659) demonstrated mathematically that a centripetal acceleration must be pulling to the center and have the form \(v^2/R\). Maybe that causal force—the centripetal force—is the one and same force that attracts the apple. Hmm?
Wait. So did the apple hit his head as we’re all taught?
Glad you asked. He never made mention of it, so it’s another fable told by supporters later. Did Washington cut down the cherry tree? Does fresh fruit always figure into Great Person Myths?
With this set of ideas, he’s way outside of the normal way of thinking. He’s violating Aristotle’s principles and he’s violating his hero, Descartes’ principle of reasoning from first principles. He’s going to work out the consequences of such a guess, without first identifying the original cause.
Here’s what he wrote of his summer many years later:
“I began to think of gravity extending to the orb of the moon & (having found out how to estimate the force with which a globe revolving within a sphere presses the surface of the sphere) from Kepler’s rule of the periodical times of the Planets being in sesquialterate proportion of their distances from the center of their Orbs, I deduced that the forces which keep the Planets in their Orbs must be reciprocally as the squares of their distances from the centers about which they revolve & thereby compared the moon in her Orb with the force of gravity at the surface of the earth & found them answer pretty nearly.”"
What’s he saying here? (I’ll bet you didn’t know that “sesquialterate” means “…in a ratio of one and a half to one.” Neither did I.)
There’s some context here that’s fun. Remember in Lesson 6) the description of the challenge brought to him from Edmund Halley, Robert Hooke (his nemesis), and Christopher Wren? The question was: if the force of attraction of the Sun varied like the inverse-square of the distance, what would be the shape of the orbit? Newton answered, “an ellipse…because I have calculated it.” But he couldn’t find the calculation and Halley had to wait? Remember? This is the essence of what Halley received in those nine pages from Isaac Newton. And the beginning of…well, everything.
10.5.1 How to Support a Moon In Its Orbit
What’s coming in the next few paragraphs is the very definition of “game changer” and you know enough to be able to enjoy it with me. Let’s develop the most important physics chapter in the book of western science, step by step.
Newton’s mental picture of rotational motion – like the Moon orbiting the Earth – was one of a jagged motion like this:
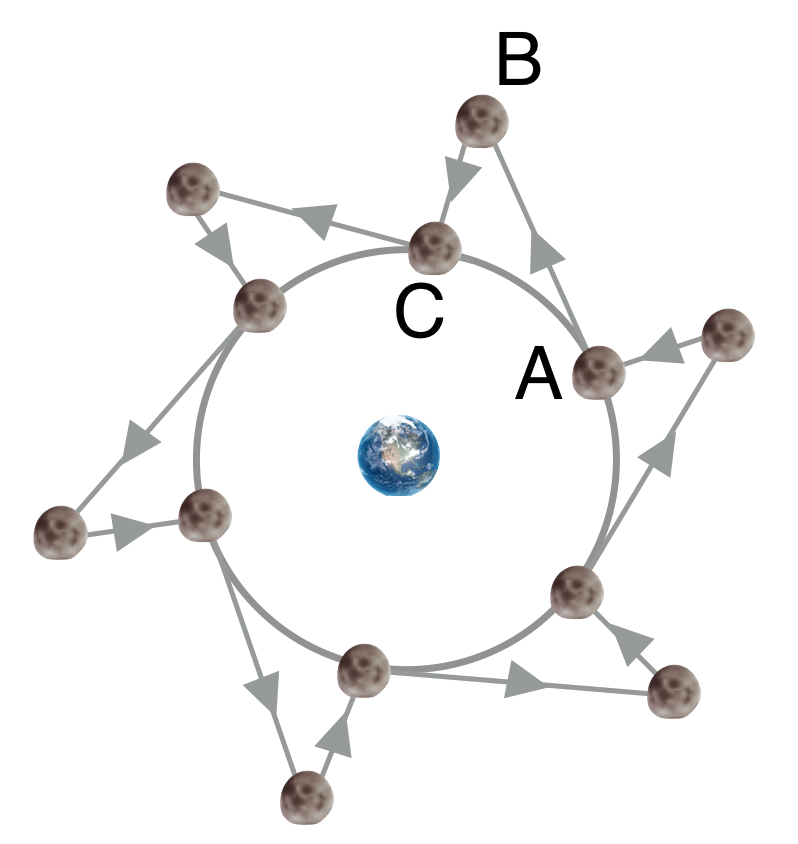
Figure 10.11: A circular orbit imagined as a sequence of straight line paths.
The Moon travels in a straight line for a bit (like AB), obeying his first law, then it’s tugged back by the Earth’s attraction (like BC) then travels in a straight line a bit…and so on all the way around.
Remember, by this point he’s got the germ of calculus in his mind so this jagged motion should approximate a circle when the little triangles get smaller and smaller. Picking out one of them labeled ABC, the AB length gets smaller and so the BC length gets smaller…keep making them smaller and the end result is that the BC length becomes zero and the AB lengths become infinite in number and a perfect circle results.
It’s this BC motion that interested him. That’s “falling” for him.
Wait. But isn’t there a force that keeps it moving in a circle. Where did that come from?
Glad you asked. Good question. If the Moon were just placed some distance from the Earth, it would start to accelerate towards the Earth (and the Earth toward it). But that’s not how the Moon was formed, rather it had some circular motion before it coalesced into the object we now see in orbit. Now Newton didn’t have a clue about the formation of the Moon (it’s even a question of active research today). But if you grant that the Moon was initially moving by the Earth and was captured by it, then you’d get the same picture as you would if it were just falling, where now that “fall” is the BC leg of this jagged journey.
What he reasoned was that when an apple falls to Earth from a branch, that the same force that causes it to fall directly down is the same force that causes the Moon’s BC motion. The Moon is successively falling as it goes around the Earth, and just missing the edge of the Earth as it does so. It’s precisely the cannon shot picture. The cannon ball falls but eventually misses and at that point it’s in orbit. I hope you can see how he quickly applied that to the Moon.
So he knows the acceleration on the Earth for the apple. If he timed an apple’s fall for, say 1 second, he could calculate how far that would be – Galileo essentially told him. The figure shows the situation, and what we want is the distance from D to E, \(y(E)\) for “Earth.”
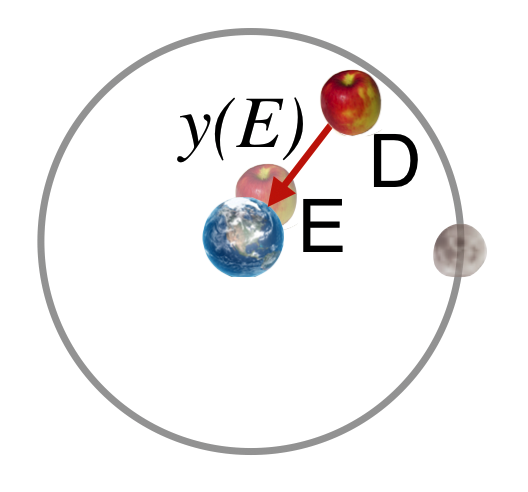
Figure 10.12: An apple falling to Earth (inside the Moon’s orbit – dare I say ‘not to scale’?).
It’s simply:
\[ \begin{align*}y(E) &= 1/2 gt^2 \\ y(E)&=1/2 (32 \text{ ft/s}^2)(1 \text{s})^2 = 16 \text{ ft.}\end{align*} \]
Remember that distance for the apple: 16 feet, or 4.9 meters in 1 second.
Now he considers the Moon’s fall. He knows quite a bit about the Moon’s motion as you’ll see. He wants to calculate how far the Moon falls in 1 second. That is, from the jagged figure above, what is that distance BC for a 1 second “Moon drop”? Seems hard to imagine, doesn’t it. Don’t underestimate Isaac Newton, he’s clever and he’s got a friend: he knew Kepler’s Third law. Let’s see how that guides him.
10.6 What’s the Moon’s Centripetal Acceleration?
This is an ingenious argument. Follow the example with your pencil out. It’s one of those moments in the history of physics where a monumental discovery is made that’s actually pretty straightforward to understand.
Here is the situation: the Moon orbiting the Earth at a distance of \(D_M\):
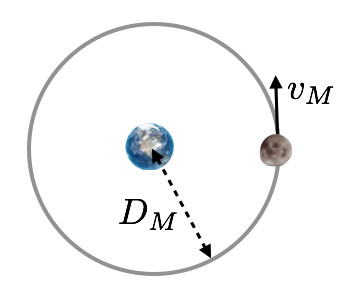
Figure 10.13: The velocity vector of the Moon is tangent to its circular path.
🖋
If it’s executing circular motion, then it has a centripetal acceleration. If it has a centripetal acceleration, then it experiences a centripetal force – his guess is that that centripetal force is due to the Earth pulling on it and if that’s the case, then that centripetal acceleration is the acceleration due to gravity – at the position of the Moon!
Is there any relation between our \(g\) on Earth and the Moon’s centripetal acceleration?
He needed to find the centripetal acceleration of the Moon using what he knows about the Moon’s motion. He knows that it takes about a month to go around the Earth and he knows Kepler’s Third law: \(T^2 \propto D_M^3\). Remember the centripetal acceleration from Lesson 6, here adopted to the figure of the Moon:
\[\begin{equation} a_C(\text{M})=\frac{v_M^2}{D_M} \tag{10.1} \end{equation}\]
How does he actually know the Moon’s speed, \(v_M\)? Well, that’s the easy part. The speed is the distance traveled — the circumference of the Moon’s orbit — divided by the time that it takes to go around, that is its period (1 month), which we’ll call \(T\). So the speed is
\[v_M = \frac{\text{circumference}}{\text{period}} = \frac{2 \pi D_M}{T}. \nonumber\]
which we can substitute into the centripetal acceleration relation, Equation (10.1) to get
\[\begin{aligned} a_C(\text{M}) &= \left (\frac{2\pi D_M}{T} \right )^2 \frac{1}{D_M} \\ \nonumber a_C(\text{M}) &= \frac{4\pi^2 D_M}{T^2}. \end{aligned}\]
Then he used Kepler’s rule from Equation (9.2) to relate the period and the radius:
\[\begin{aligned} T^2 &\propto D_M^3 \nonumber \\ T^2 &= k_ED_M^3. \end{aligned}\]
where I’ve inserted a constant of proportionality, \(k_E\), which is different from Kepler’s value which was for the planets-Sun, not Moon-Earth. Newton picked out the physics idea and applied it in a way that Kepler never intended and inserts a new proportionality constant for the little Earth-Moon system.
Substituting \(T^2 = k_E D_M^3\) for the Moon’s orbit into the denominator of the centripetal acceleration equation gives us:
\[ \begin{align} a_C(\text{M}) &= \frac{4\pi^2 D_M}{k_ED_M^3} \nonumber \\ a_C(\text{M}) &= \frac{4\pi^2}{k_E}\frac{1}{D_M^2}. \tag{10.2} \end{align} \]
Stand back and admire this! It’s an historic moment. He’s shown that the centripetal acceleration of the Moon is proportional to the inverse square of the distance from the Earth to the Moon: \(\frac{1}{D_M^2}\).
That means that the force would vary as \(\frac{1}{D_M^2}\) or more generally, \(\frac{1}{R^2}\).
Kepler thought that there was a force from the sun on the planets (magnetic!) and that it diminished as the inverse of the distance from the sun. That whatever the force is might diminish as the inverse of the square of the distance is something that many suspected about the planets, but nobody figured it out before this moment, much less for the Earth-Moon system. Keep it in mind. Newton also showed that if such an orbit (Sun-planets, Earth-Moon, Saturn-Moon!) were a circle, an ellipse, a parabola, or a hyperbola that the force of attraction would have to be? That’s right, \(\frac{1}{R^2}\).
The “inverse-squared law” is a standard thing in physics and we’ll meet it more than once as we move toward the 20th century.
🖋 📓
Please study Example 1: How fast is the Moon traveling in its orbit?
–> –> –>
10.6.1 How Newton Confirmed His Model of Gravity
Here’s one more conceptual leap required. Remember we’re worried about why an apple falls to the Earth. The left of the figure below looks like two entirely different circumstances. One of the core (see what I did there? apple? “core”?) results of his calculus is that all of the gravitational effects of an extended massive sphere are identical to the situation if the mass of that object was concentrated in a point at the center of that original sphere. Let’s shrink the Earth and do one more thing: let’s move the Moon to the original distance from the center previously occuppied by the Earth’s surface. The right figure does that with the dashed line denoting the original Earth circumference at a radius \(D_E\).
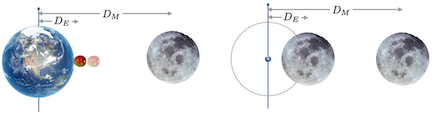
Figure 10.14: On the left, an apple peacefully falls to the surface and the Moon calmly lives in its orbit. On the right, a fanciful circumstance in which the apple is replaced with a moon orbiting at the Earth’s radius.
An apple falls, so Newton reasons there’s a force acting on it and he guesses that that force is directed to the center of the Earth. His guess is that the same force that governs the apple’s fall is the one that makes the Moon “fall” and here’s essentially his strategy to test that idea. The “Moon Argument” he called it in Principia. Here’s what he knew about the Moon:
- The velocity of the Moon, you figured out in Example 1. It turned out to be \(3.36\times 10^3\) ft/s.
- The distance from the Earth to the Moon had been known since the Greeks to be about \(60 \times D_E\) the radius of the Earth. That too had been known fairly well. The modern average number is \(D_E=20,902\) ft.
He’s already shown that the centripetal force of the Moon in its regular orbit: it’s Equation (10.1) above. This example fleshes out the conclusions that follow.
🖋 📓
Please study Example 2: Moon to Earth, including a famous quotation
🖋
If we put in modern numbers, we get that the centripetal acceleration of the Moon in its orbit is:
\[a_C(\text{M}) = 0.0089 \text{ ft/s/s}\]
Put on your seatbelt. He asked the absurd question; Suppose he moved the Moon to the radius of the Earth’s surface, what would its centripetal acceleration be? His earlier argument says that it should be larger by the ratio of the square of the distances:
\[ \begin{align} a_C(\text{E}) &= a_C(\text{M}) \times \frac{D_M^2}{D_E^2} \nonumber \\ a_C(\text{E}) &= 0.0089 \times \frac{(D_E \times 60)^2}{D_E^2} \nonumber \\ a_C(\text{M}) &= 0.0089 \times 60^2 = 32 \text{ ft/s}^2\tag{10.3} \end{align} \]
Remember that the acceleration due to gravity—how apples fall—“little \(g\)” is…Trumpets: \(g=32 \text{ ft/s}^2\)! He’s done an amazing thing!
Newton measured the acceleration of gravity on the Earth…by using the Moon!
Think about that.
He’s also shattered whatever pitiful remains are left of Aristotle’s physics. Good riddance.
This is rather remarkable and a brand new idea:
The same physical theories govern motion on Earth and the cosmos.
🖥️
Please answer Question 2 for points (there is no question 1!): The Moon feels what?
🖥️
Please answer Question 3 for points: Turn gravity off:
🖥️
Please answer Question 4 for points: Net force on the apple:
10.7 Now Think Big!
So during the plague, down on the farm in 1666 he used some incorrect numbers and was still working out the mathematics—inventing it as he went along. Even though he never published his results, he worked on the Moon idea off-and-on for years. But eventually, he started to think about the actual force that the Earth would exert on the Moon and the apple.
Now it’s model-building time with the crucial idea that the centripetal force that the Moon feels in its orbit is a “regular” acceleration. So with his Second law for the force that the Moon feels is:
🖋
\[F=m_Ma_C\] and using his derived centripetal acceleration from Equation (10.2), \[a_C(\text{M}) = \frac{4\pi^2}{k_E}\frac{1}{D_M^2}\]
we would find that the force of attraction by the Earth on the Moon is:
\[ \begin{aligned} F_{\text{Moon due to Earth}} &= m_Ma_c \\ F\text{ tentatively } &=m_M\frac{4\pi^2}{k_E}\frac{1}{D_M^2} \end{aligned} \]
But from his Third law, the Moon must exert an identical (in magnitude, but oppositely-directed) force on the Earth,
\[ \begin{align*} |F_{\text{Moon due to Earth}}| &= |F_{\text{Earth due to Moon}}| \\ & \propto M_E\frac{4\pi^2}{k_E}\frac{1}{D_M^2} \end{align*} \]
and the only way that can happen is if both forces are proportional to both masses:
\[ F_{\text{Moon due to Earth}} = F_{\text{Earth due to Moon}} = M_E m_M\frac{4\pi^2}{k_E}\frac{1}{D_M^2} \nonumber \]
Now let’s re-think the force on the Moon:
\[ \begin{align} F_{\text{Moon due to Earth}} &= m_Ma_C \nonumber \\ F_{\text{Moon due to Earth}} &= m_M \left[\left(M_E \frac{4\pi^2}{k_E} \right) \frac{1}{D_M^2}\right] \tag{10.4} \end{align}\]
in which everything in the square brackets is a constant…just a number.
The normal way of writing this is to take all of the constants in the smooth brackets in Equation (10.4) and give them a name: \(G\). And therein begins a long history of a constant of nature—still a fundamental constant: \[ F_\text{M-E}=F_\text{E-M}=G\frac{M_M m_E}{D_M^2} \]
10.8 Universal Gravitation
Satisfied that he’s on to something, he analyzed the motions of the moons of Jupiter and Saturn and eventually comets and showed that they obeyed Kepler’s Law, like Kepler’s planets and now, like the Moon. Suddenly, the whole solar system, including the moons of all planets hung together in a single mathematical system. One set of rules for the all of the celestial bodies in our visible universe and apparently fruit on our terrestrial home. But apples, planets, and moons…what’s special about them? Not much, but one quality is common to all of them: they have mass.
10.8.1 Breathtaking Leap
In Principia he made a breathtaking leap. He assumed that a gravitational attraction exists between any two objects with mass! Not just moons and planets. Right now you are being attracted by the Earth, but also by the sun, and the Moon, and Jupiter, but also…by the banana on your desk that you’re saving for lunch . All objects in the Universe attract one another according to his original planetary universal rule. For example:
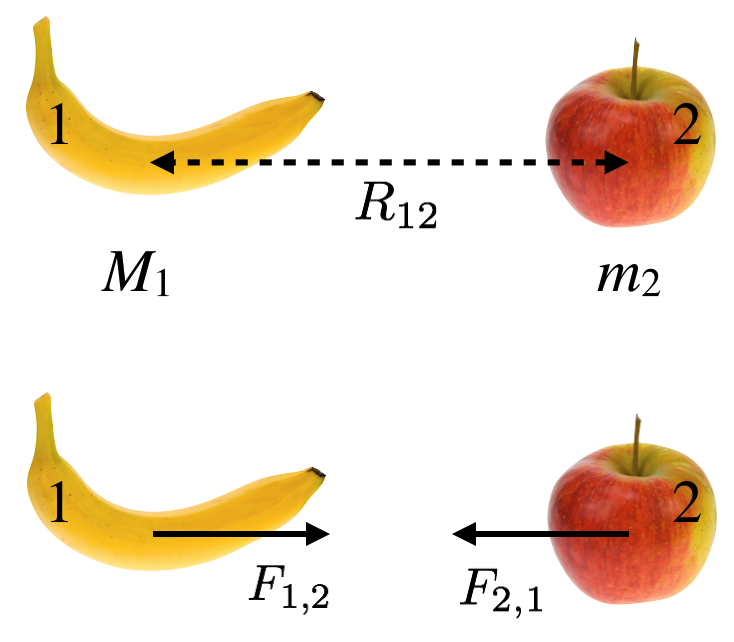
Figure 10.15: In the top, two objects, 1 and 2, with masses \(M_1\) and \(m_2\) , are a distance \(R_{12}\) from one another. In the bottom, they each exert a gravitational force on the other of equal magnitude, but opposite direction (according to Newton’s First law)
The force \(F_{1,2}\) that some object #1 with a mass \(M_1\) attracts some other object #2, with a mass \(m_2\)…and visa versa. This attraction is along a line connecting their centers which are \(R_{1,2}\) apart. The relation that describes this is just an abstraction of his original Moon rule: \[ F_{1,2} = G\cfrac{M_1m_2}{R_{12}^2},\tag{10.5} \]
the Universal law of Gravitation. The constant of proportionality, \(G\) is called Newton’s Constant or the Gravitational Constant and is very tiny and not known well. The uncertainty on that number is 0.021 out of 6.67, or about 0.3%. For a fundamental constant of nature, that’s not very precise.
10.9 The Gravitation Constant
Newton had no estimate for its value, rather he worked in terms of ratios of forces but it was measured in a laboratory by the very odd Henry Cavendish about a century later. It is a fundamental constant of nature. It. Just. Is. There’s no deriving it. Were it different by a little, our whole universe would be very different.
The gravitational force is very weak and characterized by a single constant of nature, \(G\).
Gravitation Constant: big G
\[G=6.67 \times 10^{-11}\text{ N m}^2\text{kg}^{-2}\] It’s also that collection of constants in Equation (10.5):
\[G=\left(M_E \frac{4\pi^2}{k_E} \right) \nonumber \]
Wait. What happened to \(k_E\)?
Glad you asked. Notice that our use of \(k_E\) gets swallowed up into \(G\). But there’s also \(M_E\) in there. Were we talking about, say the Earth-Sun system, then there’d be a different \(k_S\), but then the \(M_S\) would be upstairs and their ratio would still be the same as for the Earth-Moon. So the little \(k\)’s were placeholders for a bigger idea.
In Equation (10.5) the force of attraction on 1 due to 2 is \(F_{1,2}\) while the force of attraction on 2 due to 1 is \(F_{2,1}\). From Newton’s Third law? They’re equal in Equation Equation (10.5): \(F=F_{1,2}=F_{2,1}\).
🖥️
Please answer Question 5 for points: Space station weightlessness?
10.9.1 Little g Again
Now we can understand Galileo’s result from a modern point of view. With the Universal law of Gravitation and Newton’s Second law, the acceleration due to a gravitating body can be isolated from Newton’s rule by finding the “\(a\)” and the “\(m\).” To see what I mean, look at this figure:
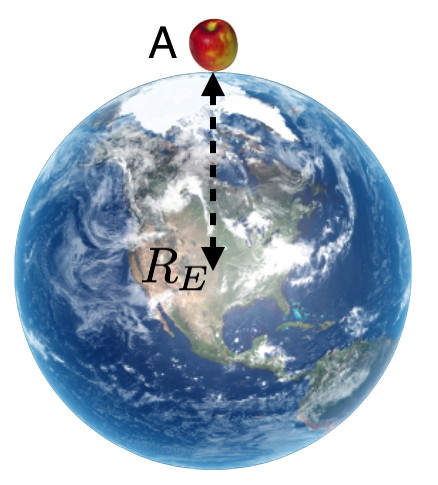
Figure 10.16: An apple sitting on top of the world.
Now you might be confused about the sudden rebranding of the acceleration of the Moon to the Earth when the Moon was brought to the Earth in Newton’s imagination. What happened to little \(g\)??
🖋 📓
Please study Example 3: What about \(g\) and \(G\)?
So in fact \(g\) is just an approximate acceleration that just happens to be the value of the Universal Gravitational acceleration for objects near the earth.
It’s where our weight comes from. The Earth attracts us with a force that’s \(F=mg\), which is a effectively a constant—on the surface of the Earth. When you step on a scale, it pushes back and is calibrated to read back how much spring-force is required to balance your weight.
Look at this drawing. (Yes, I know that’s not an apple tree. And yes, I know that trees don’t grow gigantically on the North Pole. It’s an analogy.)
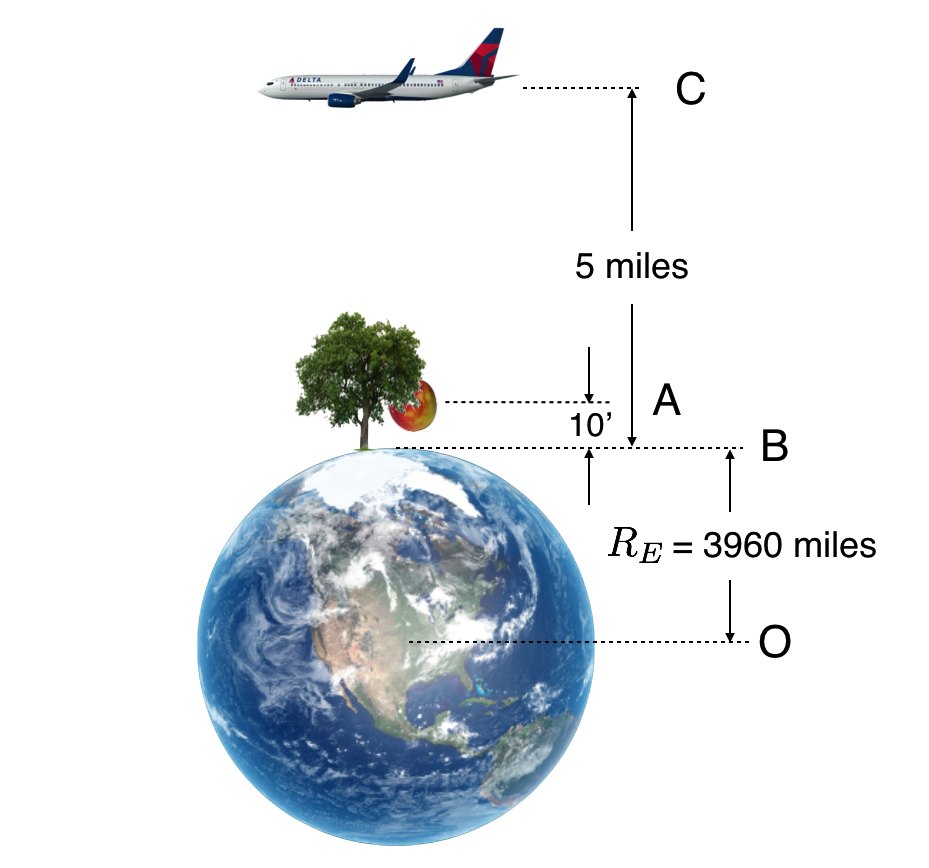
Figure 10.17: An apple, Earth, and an airplane (which might have an apple on board).
🖋 📓
Please study Example 4: An apple in a tree is further from the center of the Earth than one on the ground:
For all practical purposes? Even in a tree, the acceleration has not changed by much:
\[ a(\text{in a tree}) = g. \]
How far up do we have to go in order to see \(g\) start to get smaller? Let’s take a trip:
🖋 📓
Please study Example 5: What about as high as any of us will probably go?
🖥️
Please answer Question 6 for points: Astronauts’ weight on the way to the Moon:
🖥️
Please answer Question 7 for points: Satellite in orbit?
🖥️
Please answer Question 8 for points: Sun’s attraction to me:
10.9.2 Teachable Moment: Was Galileo Wrong?
Wait. We’ve been saying that Galileo showed that the acceleration due to gravity is a constant. Now you’re saying that it depends on how far away one is? Which is it?
Glad you asked. Yes. Galileo’s \(g\) is really not a constant, but it varies very little…even for large distances above the Earth. So for all practical purposes, we can consider it to be a constant.
Here we have a situation that’s going to repeat itself over and over in the history of physics. Galileo said that the acceleration due to gravity was constant. Then along came Newton who showed that this wasn’t right in the strictest sense: that the acceleration due to gravity varies as you move away from the gravitating object.
Was Galileo wrong?
If there ever was a Law of Nature, Gravitation was it. But then it was shown to be the case only in a restricted domain…in this case, when you’re close to the surface of the Earth. There’s really no circumstance that you or any of us (except for a handful of astronauts) will ever experience in which Galileo’s conclusion was practically incorrect.
This is the essence of a model: a model makes predictions about nature, but with the caveat that the precision of that prediction depends on one’s ability to measure.
The scenario runs like this: First, Theory A explains a feature of the world and establishes a fact of nature and a mathematical Model that uses it. Then along comes Theory B that shows that the facts and the models of Theory A are not universally applicable. Typically, the facts of Theory A and the models in Theory A are included in the facts and the models of Theory B within a domain of experience that’s smaller than the domain that Theory A describes. When this happens we’d say two things: first, Theory B is more inclusive than Theory A. It explains more about the universe and over a wider domain. And second, Theory A is still the case when applied to the restricted domain of experience that’s a subset of the domain of Theory B.
In this case, Newton’s theory (B) explains gravitation everywhere. Galileo’s theory explains gravitation only in the region near the surface of the Earth (A). We still happily—and reliably—use a constant \(g\) in the design of any structure or vehicle, for example.
In the Enlightenment, and for centuries after, if there ever was a Law of Nature, Newton’s Gravitation was it. It’s basically where the capital “L” idea for physics originated.
But, Newton’s gravitation Law…will become a “Theory” in a few hundred years at the hand of Albert Einstein.
10.10 Three Problems for Newton
The successes of Newton’s model for gravitation were many and astounding. It’s sometimes said that the Enlightenment was a direct result of his success of the naturalistic approach to explaining the world. Here are some of what his theory of gravitation demonstrated:
- He showed that the inverse-square rule for gravitation explained Kepler’s Laws, that they would accommodate circular, elliptical, and parabolic orbits. Famously, Hayley’s Comet was discovered and the predictions that Newton’s friend made were based on Newton’s rules. He simply assumed that the comet’s path was elliptical (but squashed) around the Sun as its focus and could then use Newtons’ Gravitation law. He was right…Halley’s Comet’s path takes it all the way past Neptune before it starts coming back towards the Sun. It’s a 76 year round trip.
- The Earth’s axis wobbles a tiny bit just like a top and Newton explained that, the “precision of the equinoxes.”
- He explained the twice-a-day, high and low tides as a feature of the Moon’s attraction for the ocean water closest to it as opposed to the water on the other side of the Earth from the Moon.
- Earth should not be a perfect sphere since it’s not an absolutely rigid mass. Because it rotates material closest to the axis through the poles (near the poles) would feel a different centripetal force due to the material inside of its radius from material furthest away from the axis of rotation (equator). So there should be a measurable difference in the gravitational attraction at different longitudes and this stimulated heroic teams of explorers who traveled very far north with pendulums to make measurements of \(g\) everywhere they could. Newton’s explanation worked.
- And of course his model explained all of the observed orbital motions of the known planets, a concept that was not even thought possible, or even desirable while Newton was a child. He determined the relative masses of the planets and the Sun.
Of course in addition, he had other unparalleled (including to this day) achievements:
- He properly conceived of the idea of momentum and completely described motion and dynamics.
- He correctly conceived of the theory of colors as mixing together to make white, in contradiction to the prevailing views led by Descartes.
- He invented and the pioneered the use of calculus.
By the time he died in 1726:
- Magic and superstition as explanations for nature were gone.
- Subservience to Aristotle was gone.
- Everyone believed that…everything could be known.
The very essence of the Enlightenment period in western history had begun.
But there were issues that were more philosophical that required his attention. Here are three.
10.10.1 Problem 1: Action At A Distance
Two distinct camps developed in physics. While a dominant belief in naturalism now reigned in Europe, the French followed the lead of Descartes while the British remained loyal to Newton. But everyone agreed that the actual mechanism of gravity was problematic. In a letter he wrote:
“It is inconceivable that inanimate brute matter should, without the mediation of something else which is not material, operate upon and affect other matter without mutual contact…that one body may act upon another at a distance through a vacuum, without the mediation of anything else…is to me so great an absurdity that I believe no man who has in philosophical matters a competent faculty of thinking can ever fall into it.”
Everyone agreed on the facts, but two opinions emerged about proper process. The Continental view was that until you can enunciate the mechanism of gravity and then reason deductively from that, you’re not doing acceptable science. By contrast, there was the British view—and the one that we all follow today—that what’s important is that if it works, that’s good enough.
The idea of “Action at a Distance” for any physical phenomenon bothered everyone and would today still be anathema.
But while bothered…Newton was undeterred. In many ways, Newton first differentiated the contrast between why a phenomenon occurs and how it occurs…and only an answer to how can be a mathematical model. He famously said: “I feign no hypotheses.” which even is its own Latin catch-phrase, “hypotheses non fingo” (Google it!). That’s his throw-down to the Cartesians.
No guessing, Newton’s modeling.
The bar to making progress that Descartes set up (the “Continental view”) is too high. One should “hypothesize” (I’d say model-build) and deduce empirical observables, test them and then refine your model. Then you’ve turned science into a Process that improves on its conclusions. Eventually—and gravity is a good example—one might find an acceptable why…but until that, how is good enough and makes progress possible. Descartes’ crowd could never get started and so he and his French followers were left in the scientific dust.
10.10.2 Problem 2: Stability of the Universe—Newton’s Cosmology
Newton wasn’t shy about how to apply his model. As described above, there were plenty of terrestrial and astronomical applications that were predicted and tested positive. But what about the whole enchilada? What about the whole Universe?
He recognized quickly that he faced a puzzle even more prickly than Action at a Distance. He couldn’t explain the improbability of why we’re here at all. Here’s the problem, which I can form as a question:
Is the Universe finite or infinite? His theory seems to suggest that the Universe must be infinite, with an infinite number of stars (all anyone knew about were planets and stars…no galaxies). Imagine this enormous space filled with stars, each of which is attracting every other object in it, and is in turn being attracted by every other object. The left hand picture below is a cartoon of such a situation. That one star on the right is being pulled on by everyone…and the fact that the Gravitation law varies like \(1/R^2\) means that there is an influence from all objects, all the way out to infinity. But it’s in balance since there are the same number (infinite!) of stars all around it and they are evenly distributed in all directions. So, great.
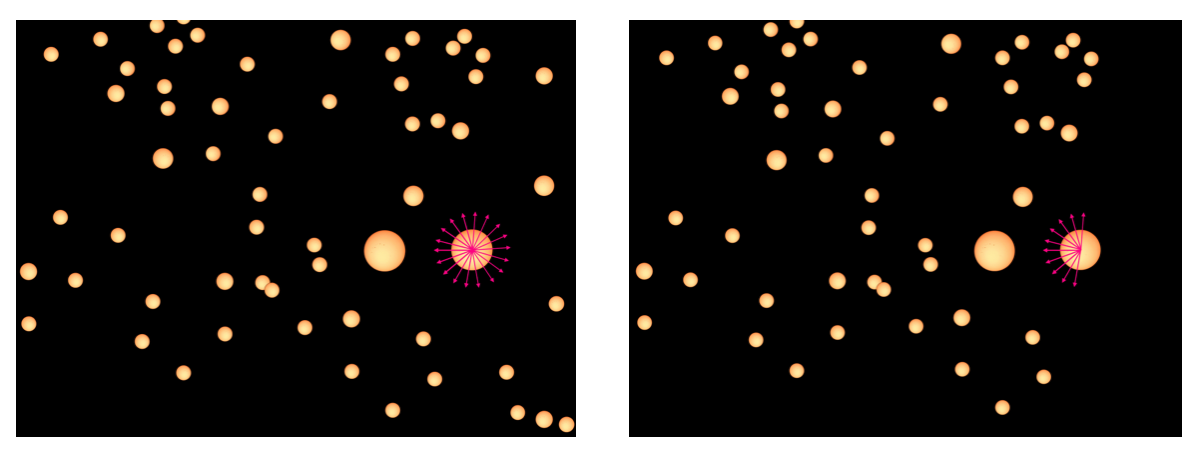
Figure 10.18: Two pictures of a universe. One that’s infinite and one that has an edge.
If the Universe had an edge, then the right hand figure would crudely be the story. Notice now that our target star is being pulled to the left and there’s no balancing set of forces to the right. That should start our star accelerating which would then pull on other stars differently as it moves and they’d start to accelerate—the end result would be a huge collapse of everything on top of itself. Yet: we’re here and so this hasn’t happened. Therefore the Universe is infinite. That’s the argument, but it’s flawed…or at least highly improbable.
Suppose the Universe is infinite and this incredibly delicate balance is at work. A butterfly could cause the whole thing to collapse, much less Jupiter orbiting the Sun. That is, the nature of his Gravitational law is such that the delicate balance that holds everything just right…has to be absolutely perfect. That seems improbable.
Newton had a famous correspondence with the leading theologian in Britain, Richard Bentley in 1692. Bentley was erudite and familiar with science and Newton took him seriously. He wrote to the reverend:
“As to your first query, it seems to me that if the matter of our Sun and planets and all the matter in the universe were evenly scattered throughout all the heavens, and every particle had an innate gravity toward all the rest, and the whole space throughout which this matter was scattered was but finite, the matter on the outside of the space would, by its gravity, tend toward all the matter on the inside, and by consequence, fall down into the middle of the whole space and there compose one great spherical mass. But if the matter was evenly disposed throughout an infinite space, it could never convene into one mass; but some of it would convene into one mass and some into another, so as to make an infinite number of great masses, scattered at great distances from one to another throughout all that infinite space. And thus might the Sun and fixed stars be formed, supposing the matter were of a lucid nature. But how the matter should divide itself into two sorts, and that part of it which is fit to compose a shining body should fall down into one mass and make a Sun and the rest which is fit to compose an opaque body should coalesce, not into one great body, like the shining matter, but into many little ones; or if the Sun at first were an opaque body like the planets, or the planets lucid bodies like the Sun, how he alone would be changed into a shining body whilst all they continue opaque, or all they be changed into opaque ones whilst he remains unchanged, I do not think explicable by mere natural causes, but am forced to ascribe it to the counsel and contrivance of a voluntary Agent.”
And again,
“The reason why matter evenly scattered through a finite space would convene in the midst you conceive the same with me, but that there should be a central particle so accurately placed in the middle as to be always equally attracted on all sides, and thereby continue without motion, seems to me a supposition as fully as hard as to make the sharpest needle stand upright on its point upon a looking glass. For if the very mathematical center of the central particle be not accurately in the very mathematical center of the attractive power of the whole mass, the particle will not be attracted equally on both sides. And much harder it is to suppose all the particles in an infinite space should be so accurately poised one among another as to stand still in a perfect equilibrium. For I reckon this as hard as to make, not one needle only, but an infinite number of them (so many as there are particles in an infinite space) stand accurately poised upon their points. Yet I grant it possible, at least by a divine power; and if they were once to be placed, I agree with you that they would continue in that posture without motion forever, unless put into new motion by the same power. When, therefore. I said that matter evenly spread through all space would convene by its gravity into one or more great masses, I understand it of matter not resting in an accurate poise.”
“… a mathematician will tell you that if a body stood in equilibrio between any two equal and contrary attracting infinite forces, and if to either of these forces you add any new finite attracting force, that new force, howsoever little, will destroy their equilibrium and put the body into the same motion into which it would put it were those two contrary equal forces but finite or even none at all; so that in this case the two equal infinities, by the addition of a finite to either of them, become unequal in our ways of reckoning; and after these ways we must reckon, if from the considerations of infinities we would always draw true conclusions.”
So Newton’s solution to this delicate balance was an appeal to God. God’s job is holding everything in place. Today we don’t do that in science.
The stability of the universe in much this same guise will come back and vex Albert Einstein and lead him into an intellectual cul-de-sac where turning around was his single, humiliating choice.
10.10.3 Problem 3: Absolute Space and Time
Newton’s mechanics led to big questions that required speculation about space and time…that is, Space and Time! He asked himself questions like this (although not this particular one).
Suppose the universe consists of only four objects: you, your friend, a rope, and a knife. You and your friend are connected by a rope. Are you stationary or are you rotating around the center point of the rope? Remember, the universe is empty but for you two. How could you tell?
This is sticky matter of relative motion. If I were to ask if you were moving linearly with respect to your friend, you could tell me that because you’d see your friend approach, pass you, and recede. Which would be really sad. (By the way, your friend would see exactly the same thing except in the other direction.) So you might not agree about who is moving and who is stationary, but you’d have no trouble believing that relative motion exists between you.
But rotation is a different matter and this question is specifically about an accelerated “frame of reference” since in order to rotate about that center point, a centripetal force through the rope would be required and so an acceleration is at work. Well, one of you has a knife and if you cut the rope one of two things might happen. Nothing! In which case you’d conclude that you were not rotating because the other thing that might happen could be that you’d immediately begin to separate meaning that: you had each been orbiting the center and that when the rope no longer connected you, you’d start straight line motion in accordance with Newton’s First law. And you’d become very lonely.
The question is…if you are rotating in this situation, with respect to what are you rotating? Newton felt that he needed an absolute measure for inertia and acceleration and he chose Space, with a capital S. Take everything out of the universe and space will still be there acting as an absolute coordinate system. All motion, constant velocity and accelerated, can be described mathematically with respect to this absolute coordinate system. To Newton, space was a thing, almost like a physical substance. Newton also insisted that there is an absolute clock…absolute Time, with a capital T.
Needless to say, there was also the Continental point of view, championed by Leibnitz who said that space was defined by the relative positions of things. Take away the things and there is no space…it’s completely relative…to stuff.
This argument is going to come back to haunt us a few more times before we reach the 21st century! But the important thing is that nobody talked like this; nobody theorized scientifically about the universe before Newton.
10.11 Cosmology Begins
This is an important point in the history of physics. It’s the beginning of quantitative, predictive science of the universe. This subfield of physics and astrophysics is called Cosmology: the study of the whole universe. (Cosmogony is another similar word that describes the origin of the universe. Formerly, thought to be outside of the province of science. Now…a regular part of physics. We tend to have expanded the word Cosmology to include origins.)
Cosmology
Cosmology is the scientific study of the large properties of the universe, including its origin, evolution, and future. Sometimes “Physical Cosmology” is used to distinguish it from religious or mythological origins stories. I prefer just plain Cosmology, where the descriptor “scientific” distinguishes it properly.
While Kepler came close, after all, he provided a formula that was descriptive of how the planets move. We understand Kepler’s law now as a logical (meaning: algebraic) consequence of Newton’s Gravitation…so it was eventually appreciated to be derivative.
Here we have Newton using an abstract (meaning: using a mathematical formula) explanation to describe the entire universe. The form of his equations insists that a gravitational force only goes to zero at infinity, so no matter how far away two objects with mass are situated, they will still attract one another. This presented a problem that needed explanation: his model was predictive, but not complete. His approach to this level of incompletion was to give up and require a deity. Our approach is to leave it open as a problem remaining to be solved. In that sense, we’re more Newtonian (“no hypothesis”) than he was!
10.12 Gravitational Energy
We say that the planets are “bound” in their orbits to the gravitational field of the Sun. That word “bound” really means what it says! If, like the Moon, the planets didn’t have their orbital motion – if they were just sitting still, they would fall to the Sun. They’re captured by it because of the infinite extent of the gravitational force. Look at the famous equation again:
\[F_{S-p} = G\cfrac{M_Sm_p}{R_{S-p}^2},\]
where here “S” stands for the Sun and “p” stands for any of the planets. That pesky inverse-square rule means that no matter how far away a planet is from the Sun, it’s always going to feel even a tiny bit of attraction. Take Jupiter out of the solar system and transport it to the Andromeda Galaxy and it will still feel the force of the Sun’s gravitational force (although of course it will feel much stronger gravitational forces from sources in its new neighborhood). Even if it’s at just a smidgen less than an infinite distance away: still a force.
Ah. But infinity is always interesting. Let’s think about this figure:
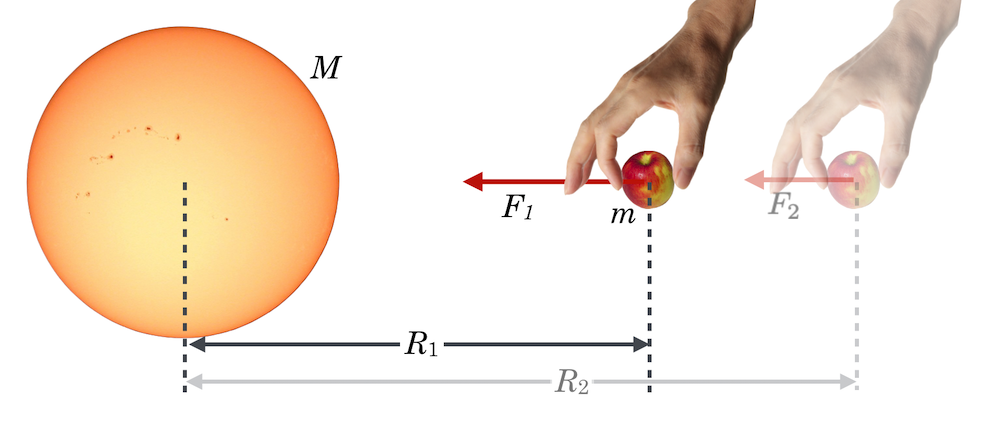
Figure 10.19: An apple in outerspace. Currently it’s at a distance \(R_1\) from the center of the Sun and it’s about to be repositioned at a distance \(R_2\).
Let’s place an apple (of mass \(m\)) at a distance \(R_1\) from the Sun’s (of mass \(M\)) center. It would feel the force of gravity from it (and the Sun from the apple) and it would have the value: \[ F=G\frac{Mm}{R_1^2} \nonumber \] Suppose we let go. What would happen?
Wait. Well, it would start to move.
Glad you asked. Right. It experiences a force and where there’s a force, there’s an acceleration, and where there’s an acceleration, there’s a change of velocity and that change would be toward the Sun.
Said a slightly different, way, in order for the apple to stay at distance \(R_1\), we’d have to hold on to it:

Figure 10.20: That apple wants to move.
Isn’t this like holding a mass above a table where it really wants to fall and could do work like drive a nail – translating its potential energy into kinetic energy and then to work?
One thing about our original \(U=mgh\) formulation of potential energy is that \(U\) depends linearly with the height. That’s because near the Earth we treated the force of gravity to be constant, so \(w=mg\) everywhere. Now we know that’s not the case, just that it’s a really (really!) good approximation. Newton taught us that the force of gravity actually changes with distance and so the gravitational potential energy will also.
So here we have the same situation. Letting go of that apple will cause it to gain kinetic energy so that were it to strike something in its way – it could translate that kinetic energy into work. Here’s what that Gravitational Potential Energy looks like:
\[U(R) = -G\frac{Mm}{R}.\label{gravpotential}\]
Wait. Um. A negative sign?
Glad you asked. Good eye. Yes, this requires some discussion and actually becomes a 21st century issue in cosmology.
The gravitational potential energy is indeed negative and here’s how we think about it.
Let’s reach in and move the apple further away to a distance \(R_2\). Would the force the apple experiences be larger than or smaller than at its original position. Of course, smaller. Here’s a logical reason to accept that negative sign. Follow along:
- When \(R_1 \to R_2\), \(F\downarrow,\) gets smaller.
- But if you released the apple at that further distance, it would gain more kinetic energy falling into the Sun than from the original position, so \(\Delta K \uparrow.\)
- But from Eq. the magnitude of \(\mid U\mid\) goes down, which is inconsistent with the kinetic energy going up.
- So \(U(R)\) must be negative so that a smaller negative number is translating into a larger kinetic energy.
Here’s the way we really think about this.
Let’s pretend (in a mathematic-y sort of way) that we can transport that apple all the way to actual infinity and let go of it. That would mean that \(R_{2}\to \infty.\) Now what happens if we just let go of it? From Newtons’ Gravitational law, \[ F=G\frac{Mm}{R_2^2} \nonumber \] when \(R_2=\infty\) the force is zero. That piece of fruit is now free of the Sun’s influence. We’d say that it’s “gravitationally unbound.” Now if that’s not creepy enough for you, let’s nudge it.
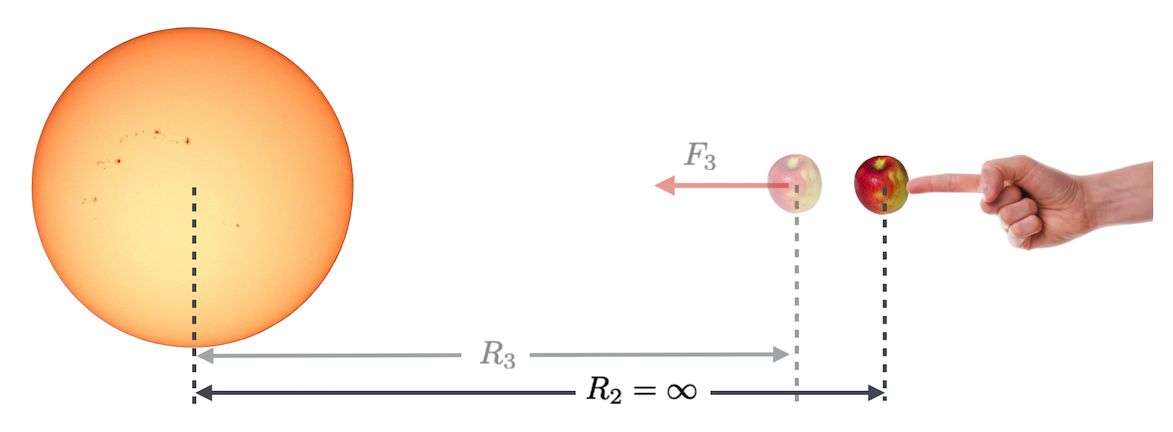
Figure 10.21: Moving that apple from infinity to just a hair less than infinity.
Imagine just gently placing it an infinitesimal distance toward the Sun to \(R_3\) just a tiny bit less than \(\infty\). While the force wouldn’t be much – it’s still a long, long way from the Sun – our lonely apple would then feel a tiny force. You know the mantra: if an object feels a force, it accelerates, if it accelerates, it increases its speed, and you can see that it will start to move slowly and then faster and faster (since the force increases at each moment) on its way toward the Sun.
🖋 📓
When we put the apple at infinity, it was unbound from the Sun, so it then has no potential energy which we can see from the gravitational potential form:
\[U(R) = -G\frac{Mm}{R}...\] Make \(R \to \infty\) and we get:
\[U(\infty)=0\]
and it’s sitting still at infinity and so it has no kinetic energy;
\[K(\infty)=0.\]
So, what’s its total energy, \(E_T\)?
\[E_T=U(\infty)+K(\infty)=0+0=0.\]
Energy is conserved! So if that’s the energy at infinity, then every point after it’s nudged should also have zero total energy. Here’s the energy conservation relationship for any point (any arbitrary \(R\)) along the path back to the Sun
\[E_T=0=U(\infty)+K(\infty)=U(R)+K(R).\]
We all agree that kinetic energy is always positive, and so the gravitational potential energy must be…negative. Here how this works in our time-honored, thermometer diagram especially suited for conservation situations.
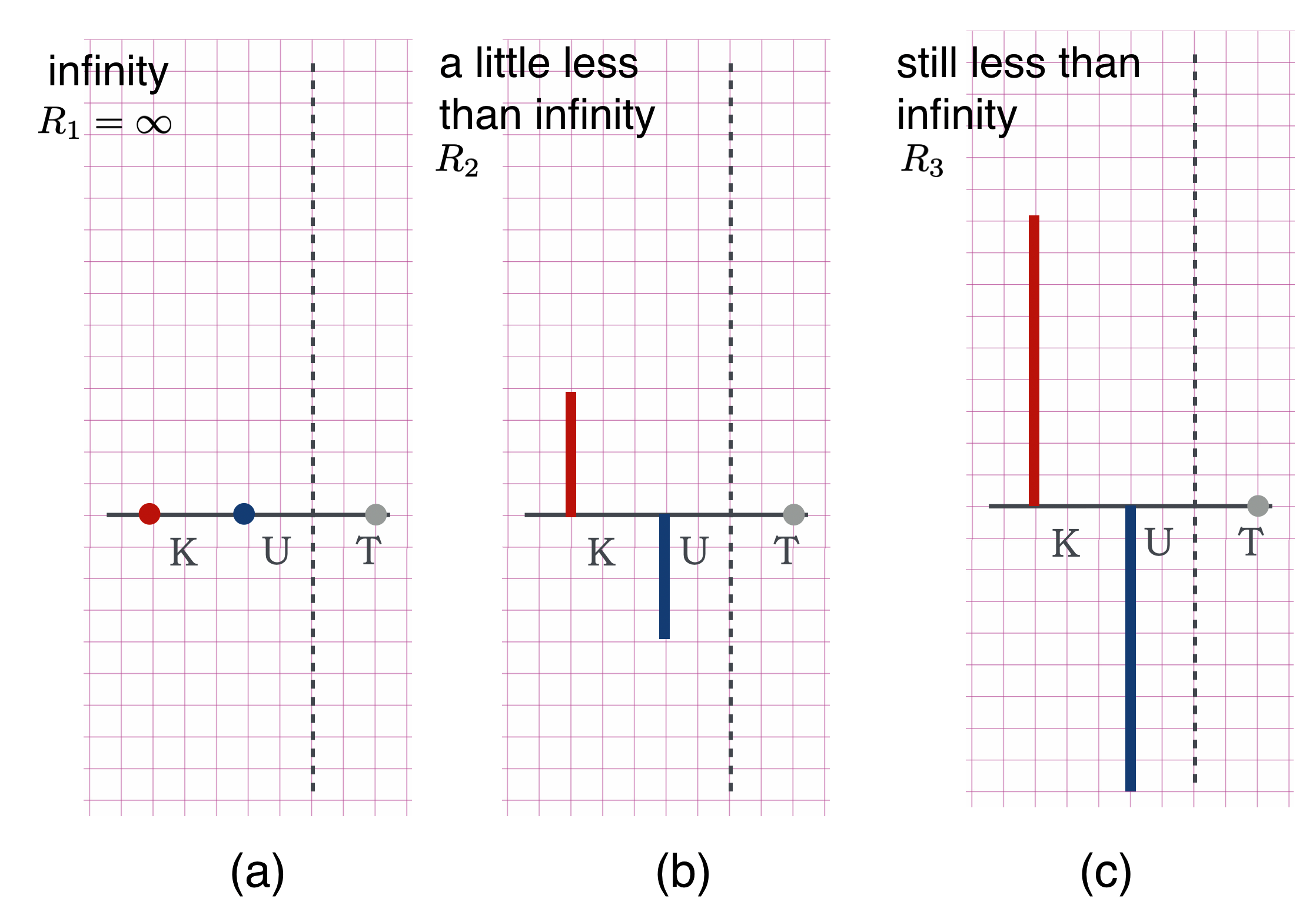
Figure 10.22: Kinetic plus Potential energies always cancelling at three different locations away from the Sun to give a total of zero energy at each.
The actual functional forms of these are also instructive:
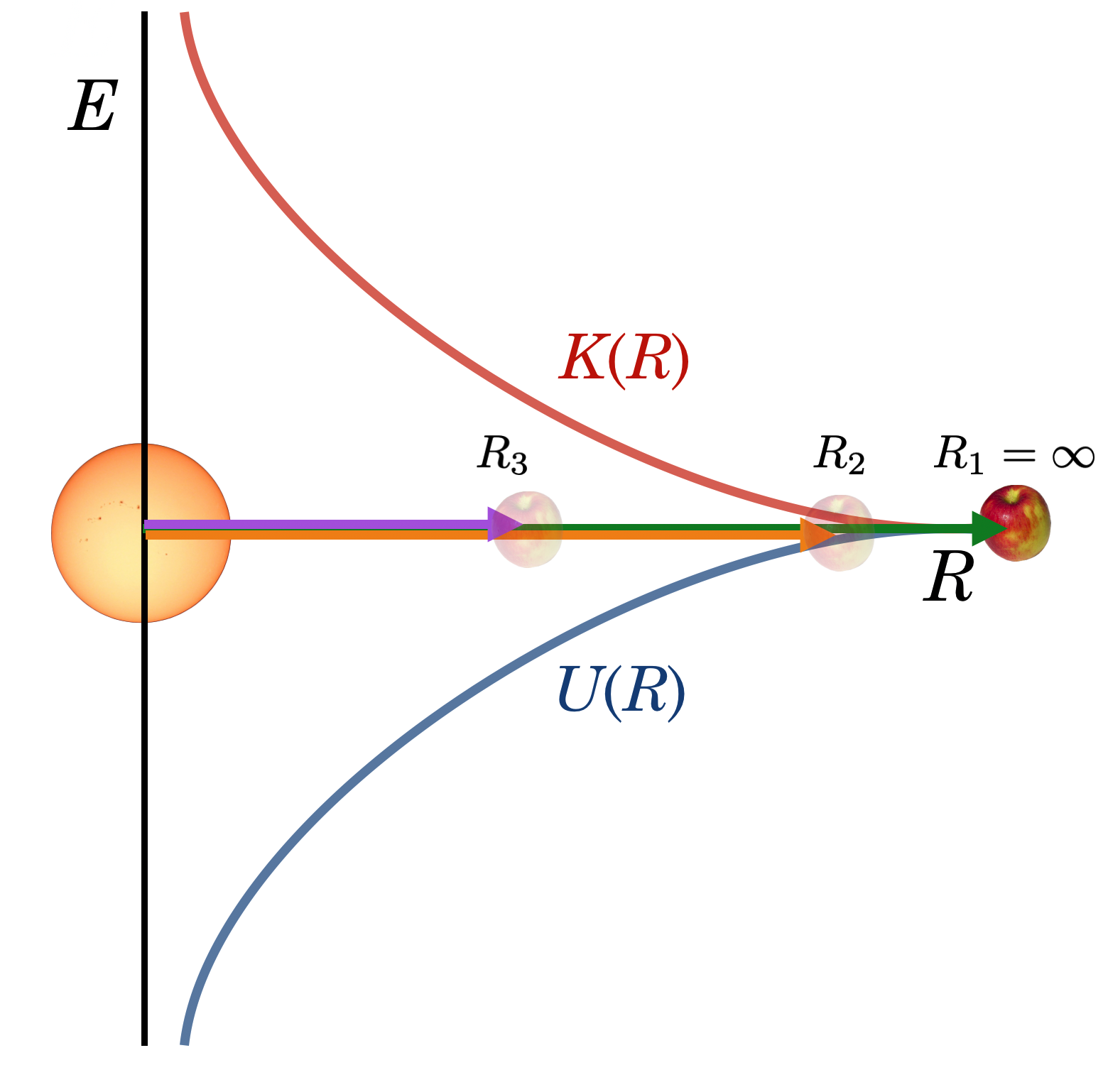
Figure 10.23: Kinetic and Gravitational Potential energies on the same graph…always summing to zero from infinity for each of the positions in the previous plot.
–> –>
📺
You might benefit from gravPotentialEnergy_v2.mp4 for review and wrap-up of these sections.
{: .dealclass}
10.13 What to Remember from Lesson 10
10.13.1 The Galileo Story
It’s sad, it was maybe inevitable. But he accomplished a handful of things during this post-Padua time in his life:
- Of course the mechanics that we’ve discussed were done before this, but it was only under house arrest that he smuggled out to Holland the publication that established his important work.
- He didn’t invent the telescope and his Moon observations where not unique to him but he “published” first and in a way that got everyone’s attention.
- His patient and detailed Jupiter, sunspots, Venus, and star observations – and publication – stunned the world and were indeed unique to him.
- His Letter to the Grand Duchess threw down the gauntlet about the relationship between the Church and scientific observation and modeling, sure. But it was also an important challenge to any authority that puports to regulate and restrice scientific facts through either dogma or political authority. We need to remember Galileo’s letter in the United States as we’ve slipped three and a half centuries in that regard.
10.13.2 Newtonian Gravitation
The Universal law of Gravitation was the single enunciation about how the world works that created modern science. His three laws of motion were important, sure. But Gravitation established forever more that there is one kind of rule for how things work and that single rule works on the Earth and in the heavens. Nobody ever went back to the old way.
Just to recap, for any two objects, “1” and “2”, the force between them is attractive and is: \[ F_{1,2} = F_{2,1} = G\cfrac{M_1m_2}{R_{12}^2}. \nonumber \] where
\[G=6.67 \times 10^{-11}\text{ N m}^2\text{kg}^{-2}\]
is the Gravitational Constant or Newton’s Gravitational Constant.
The Gravitational Potential Energy experienced by a massive body due to another is negative and is:
\[U(R_{12}) = -G\frac{M_1m_2}{R_{12}}.\]