Lesson 9 Early Cosmology
Wrestling With the Planets
9.1 Contents
9.2 Goals of this lesson:
- Understand
- Be able to explain what the important predictions were from Copernicus’ model and how they were confirmed.
- Be able to explain how Kepler’s, Tycho’s, and Copernicus’ models of the solar system are different.
- Appreciate
- The ancient and Hellenistic Greek models of the solar system.
- The Ptolemaic model.
- Be familiar with
- The lives of Copernicus, Kepler, and Tycho.
- The importance of Tycho’s systematic approach to measurement.
9.3 A Little Bit of Kepler
One of the most interesting and courageous scientists of the 17th, or maybe any century, was the German Johannes Kepler (1571 - 1630). His personal life consisted of one disaster and tragedy after another. His professional relationships ranged from tempestuous to subservient. His first non-royal employer, Tycho Brahe, was a tyrant and upon his death, Kepler “liberated” Tycho’s extensive observational data on the orbit of Mars and fought the Brahe family in and out of court for years. His relationship with Galileo was adolescent: Kepler always cheerful nearly begging for notice from the then famous Italian. Galileo basically ignored him unless he wanted something.
Kepler was continuously sick, perpetually destitute, a magnet for personal tragedy, formed by an awful childhood, lived in terrible environments, and was aggressively self-loathing.
“That man has in every way a dog-like nature. his appearance is that of a little lap-dog. Even his appetites were like a dog; he liked gnawing on bones and dry crusts of bread, and was so greedy that whatever he saw he grabbed; yet like a dog he drinks little and is content with the simplest food…He is bored with conversations, but happily greets visitors like a dog; but when something is snatched from him, he sits up and growls. He barks at wrong-doers. He is malicious and bites people with sarcasms…He has a dog-like horror of baths…” Self-description at 25 years of age.
The single common feature of Kepler’s adult life was the terrible Thirty Year’s War which killed as much as a third of the German population. Whole towns would switch allegiance to Catholicism or Protestantism overnight depending on which army had passed through last. Kepler as a Protestant, was sometimes tolerated and sometimes evicted.
He was incredibly prolific, writing many books on astronomy, mathematics, and optics. He wrote one of the first science fiction novels, a third-person autobiography and left volumes of correspondence with intellectuals and political leaders from all over Europe.
He was educated to be a Lutheran minister, but stumbled into astronomy and mathematics and learned Copernicanism outside of classes with one of the early supporters. He graduated but because of prodigious mathematics skills he became an atrocious math teacher at the Protestant school in Graz.
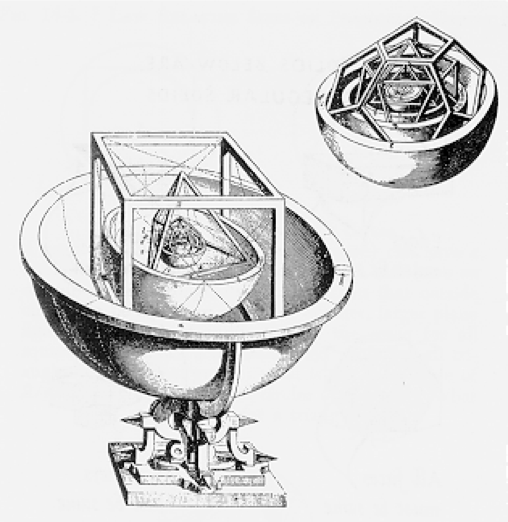
Figure 9.2: From Mysterium Cosmographicum showing how the different geometrical solids nest together with the orbits surrounding their inside and outside dimensions. Kepler commissioned a jeweler to make a solid model of the whole contraption.
He was plagued by many questions in astronomy: Why are there six planets? Why do the speeds of the planets decrease the further away from Earth? Why are they ordered in the way they are? He was obsessively detailed in his scientific writings and so we know that on July 9, 1595, while he was boring himself to death in his own lecture, he had a sudden realization. He thought he’d come on a beautiful description of the planets’ spacing. There are five so-called Platonic solids—all others can be broken down into combinations of the five: cube, dodecahedron, icosahedron, octahedron, and tetrahedron. What he found—he thought—was that if one imagined a sphere on the outside of each of the centered, increasingly bigger, and nested shapes in the order, octahedron, icosahedron, dodecahedron, tetrahedron, and cube…that the radii of those spheres correspond to the relative radii of the planets. Numerically, it was close. The figure above is the famous rendering that he inserted by hand in his eccentric 1596 book, Mysterium Cosmographicum (The Cosmographic Mystery). It’s madness of course. But in a nice way. Kepler’s writing style was unusual, essentially a narrative, describing his highs and his lows. His passionate enthusiasm was naive-sounding, but it was who he was.
“It is amazing! …although I had as yet no clear idea of the order in which the perfect solids had to be arranged, I nevertheless succeeded…in arranging them so happily… Now I no longer regretted the lost time. I no longer tired of my work; I shied from no computation, however difficult…day and night I spent with the calculations to see whether the proposition that I had formulated tallied with the Copernician orbits or whether my joy would be carried away by the winds…within a few days everything fell into its place. I saw one symmetrical solid after the other fit in so precisely between the appropriate orbits, that if a peasant were to ask you on what kind of hook the heavens are fastened so that they don’t fall down, it will be easy for thee to answer him.” Farewell! (Kepler, Mysterium Cosmographicum)
Not your standard scientific writing.
While this work was mostly fanciful at best, it set the stage for a number of similarly manic publications in understanding the motions of the planets that rhetorically meander their way to world-changing conclusions. He started working out the questions that needed to be asked.
“If we want to get closer to the truth and establish some correspondence … between the distances and velocities of the planets then we must choose between these two assumptions: either the souls which move the planets are the less active the farther out the planet is removed from the sun, or there exists only one moving soul in the center of all of the orbits, that is the sun, which drives the planet the more vigorously the closer the planet is…”
It’s not a spoiler to note that the idea of a force from the Sun in Newton’s hands led to our classical idea of gravity. Kepler was the first to imagine such a thing, a generation before Newton.
Wait. Doesn’t this sound like Gravity as we’ve all learned it?
Glad you asked. Yes, and that’s one of the neat things about Kepler: he was imaginative and ahead of his time in many ways. He envisioned that the Sun pulled on the planets with what he called a “Soul” but he also imagined that there needed to be a force pushing the planets around their orbit, and there he was mistaken.
The year after Mysterium, he married a rich, twice-widowed woman and began a family. Within two years their first two children perished, Graz was overthrown, and he and his family had to leave. It was in 1600 when he and Tycho Brahe’s paths crossed. By this time Tycho had been evicted from his island laboratory and moved his entire circus to Prague. As we’ll see later, Tycho hired Kepler and assigned him the “problem of Mars.” Kepler predicted that he’d work out the details of Mars’ orbit in 8 days and he succeeded, but 10 years later. This he did, by basically stealing the data in the immediate aftermath of Tycho’s death.
“I confess that when Tycho died, I quickly took advantage of the…lack of circumspection…of the heirs, by taking the observations under my care…”
Kepler got Tycho’s old job in 1601 as the Imperial Mathematician to the Holy Roman Emperor, His Highness, Rudolf II…who was quite unstable. He spent the rest of his life trying to actually collect his salary, which became years in arrears.

Figure 9.3: A NEW ASTRONOMY Based on Causation or a PHYSICS OF THE SKY derived from Investigations of the MOTIONS OF THE STAR MARS Founded on the Observations of THE NOBLE TYCHO BRAHE. Kepler’s Big Score.
Analytic geometry had not been invented when Kepler began working on the Mars orbit, so he relied on geometry, spherical trigonometry, and the newly invented logarithms, which can be used to simplify multiplication and division of large numbers (a slide rule is based on logarithms). Think about what he had to do. Tycho had thousands of individual position measurements of where Mars appeared as measured from Earth. We know that both the Earth and Mars are moving relative to the sun. Kepler’s research program—as a good Copernican—was to translate those data fro an Earth vantage point into Mars’ trajectory as viewed from the Sun. That’s a really hard calculation! It took him six years of heroic calculations. He struggled with circles—which didn’t work—then with an oval (!)—and then finally realized that the trajectory was an ellipse. He finally admits, in his Kepler-kind of way in Chapter 60 of his 1609 book, Astronomia Nova (New Astronomy):
“Why should I mince my words? The truth of Nature, which I had rejected and chased away, returned by stealth through the backdoor…I thought and searched…as to why the planet preferred an elliptical orbit…Ah, what a foolish bird I have been.”
This is one of the most important books in the history of astronomy. In it he enunciates two of “Kepler’s Laws,” which we’ll talk about below. But he also—for the first time in 2,000 years of recorded history—asserts that planets do not move in (the perfect) circles that everyone believed was absolutely required of the cosmos. Think about how intellectually courageous this was, just a few years before Galileo was severely punished for an even more revolutionary opinion than this.
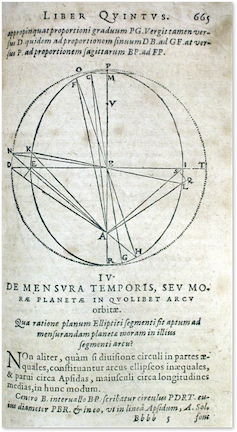
Figure 9.4: From Astronomia Nova showing one of Kepler’s diagrams comparing an ellipse with a circle and the small deviations that were the clues to his discovery.
In 1611, Kepler’s son died, as did his wife. Rudolf abdicated and his successor was not supportive and so Kepler had to move with his remaining children, this time to Linz. There he advertised for and set up interviews for a new wife, “hired” one, and had six more children.
But the weirdness never ends for Kepler: In 1616, his mother was accused of witchcraft and by 1620 the charges were so serious that she was in danger of torture and execution—eight women had been executed so far. Kepler dropped everything and moved from Linz to Leonberg, more than 500 km away and essentially became her defense attorney. He won the case, but not until a year had gone by.
In 1619, amid all of the disruption that was his life, he published Harmonice Mundi (Harmonies of the World). His mission was to understand the relative periods—how long it took for a planet to orbit the sun—and see if there was any pattern. Ever the mathematical-romantic he likens their motions to musical influences— the phrase “music of the spheres” comes from Pythagoras and was a way to emphasize what he and then Plato were convinced was an overall harmony of the celestial motions. Out of this conviction of harmony, or symmetry, came what we now call Kepler’s Third Law, which we’ll talk about below. This was a crucial motivation for Newton’s gravitational theory. Kepler found a pattern that all of the planets exhibit that relates their orbital periods to the distances that they were from the Sun.
His fight with the Brahe family resulted in a settlement that required him to publish Tycho’s data. He undertook this using his own funds, and so of course the printer’s facility burned to the ground in the process.
Kepler’s ability to rebound and find work was impressive, but sometimes he made judgment mistakes. His last employer was on the wrong side of a political divide and Kepler had to set out again looking for him in order get paid. The last we see of him, he is slowly and painfully riding a horse into the rough country of continuing warfare. He never made it, dying from illness on November 15, 1630 far from home in Regensburg, Germany. His final resting place, a church graveyard, was ravaged by the Swedish army and there is no remnant of his remains. Of the 12 children that he had by his two wives, only two survived.
Kepler is considered among the greatest scientists. In 1949 Einstein considered writing a biography of him—there are many, since he was such an appealing figure. He described Kepler as one “…who had devoted himself passionately to the pursuit of deep insight into the nature of natural incidents, and who, despite all inner and outer difficulties also reached his high aim.”
“In 1930, he wrote, “In anxious and uncertain times like ours, when it is difficult to find pleasure in humanity and the course of human affairs, it is particularly consoling to think of such a supreme and quiet man as Kepler. Kepler lived in an age in which the reign of law in nature was as yet by no means certain. How great must his faith in the existence of natural law have been to give him the strength to devote decades of hard and patient work to the empirical investigation of planetary motion and the mathematical laws of that motion, entirely on his own, supported by no one and understood by very few.”
Today we would call Johannes Kepler an astrophysicist, or a theoretical astronomer. He didn’t make observations, but he used (new) mathematics—inventing additional formalisms along the way—to interpret the data and make predictions.
But we’re ahead of our current story. Let’s turn the clock all the way back to the first scientists who thought deeply about the sky and recorded their thoughts. Of course, the Greeks.
Wait. Kepler seems like a sad guy.
Glad you asked. His life was a perpetual tragedy, surrounded by an unimaginably horrid war among neighbors. There is an old, but really gripping biography of him that’s very well known and somewhat controversial that you might enjoy, Arthur Koestler’s, The Sleepwalkers. It started out as a biography of Kepler, but in later form covered the cosmology of the Greeks, Copernicus, Kepler, Brahe, through Galileo (whom he didn’t like at all).
Here’s a different look at Kepler:
9.4 Ancient Astronomy
Admit it: everyone is awestruck by the spectacle of the sky on a dark night. It’s a basic human instinct and it links us to our ancestors of thousands of years ago. The rhythm of the variously repeating objects in the sky were easily mapped onto people’s everyday lives which also had daily, monthly, seasonal, and annual rhythms. It’s not hard to appreciate that they might have taken the sky’s patterns as responsible for Earthly events and so people put a lot of thought into it! As a result, Astronomy is probably the oldest intellectual activity in all of humankind. By questioning the skies, we evolved into modern scientists with our current need to understand all of the physical universe!
Wait. But what about astrology?
Glad you asked. Astrology is…unfortunate. When it’s used to make predictions or analyze a personality it means that someone is pretty guilible. And that an angel has lost his wings.
While most of us have not looked at where the planets and stars are night by night, month by month, recording these positions and motions was a serious activity for the Babylonians, Egyptians, and Greeks. The regular motion around what we would call the North Star15 as shown in a time-lapse image in the figure below was highly predictive but the motions of the planets, notsomuch. In fact the word “planet” comes to us from the Greek meaning “wanderers” which is what indeed the planets seemed to do.
Basically there are three kinds of regular objects and three sorts of motions: the background stars which were familiarly constant year after year; the planets, which were relatively constant, but which executed odd motions every once in a while; and the Moon and Sun which seemed to execute their motions daily with subtle variations. Eclipses were frightening events, although information from the Babylonians enabled pre-Socratic Greeks to predict when they might occur. Comets were likewise startling, but supernovae, while few and far between, must have been deeply troubling.

Figure 9.5: This is a long exposure of the sky around the North Celestial Pole, our North Star. The traces do suggest a circular path for each star, but we know it’s actually indicative of the Earth’s daily rotation on its axis.
While the Babylonian scholars were terrific recorders of events, the Greeks seemed to be the first to actually try to explain the cause of the stars and planets’ motions. The difference between “description” and “explanation” is evident, even if their results are hard to swallow.
9.5 Greeks, Measuring Stuff
Explaining motions in the sky for the Greeks came with conceptual baggage–“theory-laden” would be the philosopher of science’s term to describe their models. The mathematicians of the Pythagorean school greatly influenced Plato, for whom everything is a poor copy of otherwordly: you can draw a circle, I can draw a circle, but for Plato and his followers there is only one True Circle, and that’s the Ideal one. Circles were perfect in every respect–no matter how you orient them, they’re identical, which you can’t do with any other shape. So naturally (?) celestial motions had to be circular. Any explanation of the motions of the stars, Moon, and planets had to take this restriction as the starting place until our brave Johannes Kepler cast circles aside in the 17th century.
Look at the star trails above, a time-lapse photograph of the stars through a night. They appear to follow perfectly circular paths around the North Star.16
So it’s easy to believe that this observation on top of your predisposition to really liking circles, would lead Plato and others to extrapolate that motion to everything “up there.” Likewise, the Sun’s and Moon’s motions are arcs through the sky and also look to be close to circular. There was enough visual evidence that the Earth was a sphere (just a circle in 3 dimensions, right?)—understood a century before Plato and required by Aristotle.17 The explanation that emerged placed the Earth at the center of the Universe with all of the celestial objects in circular orbit around it.
📺
You might benefit from sky1greeks2.mov for an overview of the sky from an on-line planetarium.
{: .dealclass}
9.5.1 Describing and Explaining
🖋 📓
What did the Greeks observe? Well, of course they observed essentially the same things that we observe and the same things that the Babylonians and Egyptians observed. The Babylonians had a lot of data, but all they did was describe what they saw. The Greeks were the first to actually try to explain what they saw and for them, this was a job for Philosophers and Mathematicians. This is where they were first: using mathematical (meaning: geometrical) arguments to learn facts about the heavens. There were intellectual giants who set themselves on this task from the period between Plato (roughly 425 - 347 BCE) in Athens and Ptolemy (roughly 90 - 168 CE) one of many Alexander the Great’s cities called Alexandria…the one in Egypt.
Among their accomplishments were: * a determination of the radius of the Earth, which was pretty close; * an understanding of solar eclipses as a near-perfect blocking of the Sun by the Moon; * an estimate of the distance from the Earth to the Moon (\(D_M\)) in terms of the radius of the Earth (\(R_E\)): about, \(D_M = ~60 \times R_E\); * the creation of a very large and sophisticated star catalog, of course just positions of the stars as there were no telescopes.
The Greeks were very clever and invented the idea of not just describing Nature but trying to explain phenomena by interpreting measurements using mathematics. Explanation required some mechanism.
Wait. I gotta say that I don’t get retrograde motion. You need to do a better job.
Glad you asked. Hmm. Manners much? Okay. Here’s a clip of an old video that I made that shows another way of viewing this.
📺
Go to retrograde for review and wrap-up of these sections.
{: .dealclass}
9.5.2 About Those Circles
How did all of those celestial objects execute those motions? The first to publish a mechanism was a contemporary of Plato’s and another of the geometry giants of classical mathematics, Eudoxus of Cnidus (roughly 408 BCE - 355 BCE). He calculated that the stars, planets, the Sun, and the Moon were all attached to material spheres that rotated around axes that went through the center of the Earth. We can see through them, so he presumed that they were made of crystal: the “Crystalline Spheres.” Because many of the motions were somewhat irregular and complicated, he needed many spheres with their axes of rotation inclined differently among them all. For example the Moon’s motion alone required three such spheres to simulate the monthly and daily rotation and then a third to account for the fact that its orbit is slightly inclined to the horizon. Aristotle inherited this idea but took it a step further. Eventually his cosmos required 55 spheres, including one for the entire outer shell to which the stars were all thought to be collectively attached.
Make no mistake. This was not just mythology, although there was some of that in the naming of constellations. This was an attempt to describe what was actually happening. We know that because physical mechanisms were postulated in order to explain why adjacent spheres don’t rub against one another and impede the motions—he incorporation of little “ball bearing” like idler wheels were thought to be between spheres insuring smooth independent rotations. This was an idea of Aristotle’s.
🖋 📓
This model struggled to explain the data in three particular ways.
First, Venus and Mercury seemed to be related to the Sun, always very near it. That seemed hard to understand if the Sun, Mercury, and Venus all rotated around the Earth.
Second, Venus seemed to change its brightness in ways that no other planet did.
And, third, some planets appeared to suddenly go backwards!
This latter behavior is called “retrograde motion” and was very confusing. If you watch, say Mars (which is particularly obvious) night after night at the same time, it would appear to advance one way with respect to the background stars, and then reverse and advance the other. In the picture below, imagine that each row is a successively later (over days) observation of Mars (\(\odot\)) at the same time each night in relation to three background stars (\(\star\text{A}, \star\text{B}, \text{ and } \star\text{C}\)). In the first observation (top row), Mars is to the left of \(\star\text{A}\). Notice how,at the same time on successive nights (each row), Mars appears to move farther to the right relative to the background stars. But on the fifth observation…say a week or so later, that it starts appearing to move back to the left. Then, a few nights later, it turns around and goes back the way it originally was moving.
\[\begin{aligned} \odot \;\;\;\; &\star\text{A} & &\star\text{B} &\star\text{C} &\\ &\star\text{A} \;\;\;\;\;\;\;\;\;\;\; \odot & & \star\text{B} &\star\text{C} &\\ &\star\text{A} & &\star\text{B}\;\;\;\;\;\;\;\;\;\;\odot &\star\text{C} &\\ &\star\text{A} & &\star\text{B} &\star\text{C} & \;\;\;\;\odot \\ &\star\text{A} & &\star\text{B} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\odot &\star\text{C} &\\ &\star\text{A}\;\;\;\odot\;\;\;\;\; & &\star\text{B} &\star\text{C} &\\ &\star\text{A} & &\star\text{B}\;\;\;\;\;\;\odot\;\; &\star\text{C} &\\ &\star\text{A} & &\star\text{B}\;\;\;\;\;\;\;\; &\star\text{C} &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\odot\end{aligned} \]
Retrograde motion happens with all of the planets and it’s of course a function of our observing from the Earth. But the spheres couldn’t account for this bizarre behavior since they would have intersected with one another!
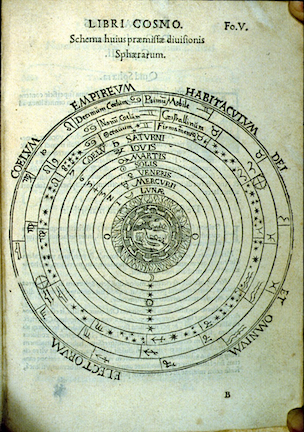
Figure 9.6: An engraving from the German mathematician and artist, Peter Apian, from a 1551 French edition of his 1524 Cosmographicus liber. Copernicus would surely have been very familiar with this popular book.
Nonetheless, the spheres-picture that came from Aristotle’s school was dominant. When Christianity took hold the Earth became the focus of everyone’s attention. When Thomas Aquinas (1227-1274) merged Catholic dogma with the all-the-rage Aristotle’s philosophy Aristotelian picture was actually embedded into Church doctrine. The figure above shows a 1534 engraving by Peter Apian which conformed to the Christian cosmology: all planets, the outer stars, the Sun and the Moon revolving around the Earth. The crystalline shells were a part of the reality-picture in the Aristotelian-Church model.
🖥️
Please answer Question 1 for points: Thinking about retrograde motion
9.5.3 Ptolemy
The original Greek-astronomy state of affairs lasted until a Greek-Roman-Egyptian by the name of Claudius Ptolemaios (“Ptolemy”) of Alexandria (approximately 90 CE – 168 CE), Egypt built a new model. We know him by his Roman-citizen’s name, Ptolemy, although he was Greek and worked in the amazing city of Alexandria, Egypt. His goal was different from his predecessor Greeks, and this is important: he wasn’t trying to explain how the planets moved, but was trying to build a model that would accurately calculate where they would be at any time. This is an important distinction.
🖋 📓
The figure below shows a model…of his model. The big circle is the planet’s main trajectory around Earth called the “deferent.” But the planet doesn’t ride on that circle, rather it revolves around a little circle – an “epicycle” – the center of which revolves around Earth, riding on the bigger circle. So all of the planets, the Sun, and the Moon all have epicycle parameters where he changes the sizes of the deferent and the rotational speeds to match what he saw. This idea of “epicycles” stays in astronomy until the early 17th century.

Figure 9.7: From left to right, the motion of a single planet around the Earth is shown where the planet “rides” on a little circular orbit (an epicycle) which in turn has a center that’s attached to a bigger circle (the deferent) going around the Earth. In this way, one can imagine periods in which the planet would appear to be going the other way, as seen from the Earth
Ptolemy was a good observer who took careful measurements of the positions of every object and the times of those observations. In fact his data were the best until the 17th century! Increasing precision showed him that his model needed tweaking, and so tweak he did: the figure on the right shows that the center of the deferents for each planet were not required to be at the center of the Earth—rather at a position offset from Earth, the “equant”—and furthermore the rates at which the individual epicycles moved around the deferents were not required to be uniform. Otherwise, his model would not match what he saw.
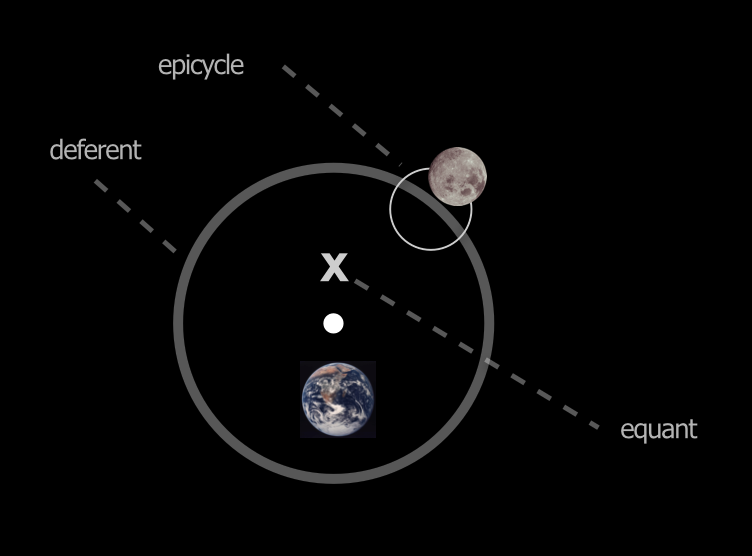
Figure 9.8: The addition of the equant and even non-uniform rate of motion was required in order to fit the data.
Ptolemy’s scientific work was far-reaching beyond astronomy, but it was his model that stood the test of time, indeed, 1500 year’s worth of time. The Arabs called his text, Almagest, meaning “the greatest” and it followed them into Spain, where it was eventually translated into Latin around the 14th century. The next figure shows a sketch of the whole solar system as he modeled it.
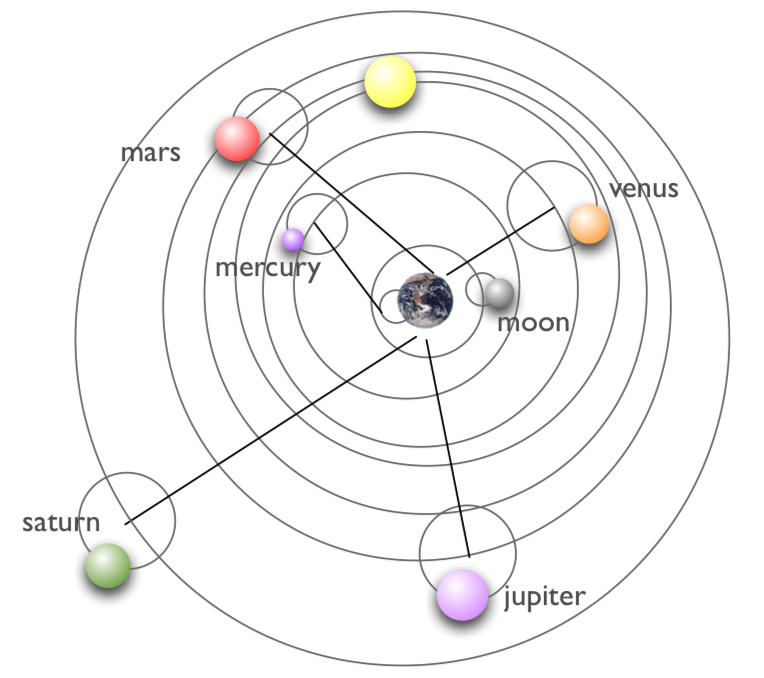
Figure 9.9: The Ptolemaic model of the solar system. The Sun is the yellow sphere, between the orbits of Venus and Mars.
If what you want is an accurate prediction of various astronomical or astrological events and you lived before 1600, then Ptolemy’s model is what you needed. You just turn the crank with all of his little circles moving mathematically at their individual rates, and out would pop the positions of everything. And since many agricultural and religious events were timed by particular, near-annual astronomical events, it mattered to you.
Wait. You mean that there was the model of planets in spheres and the model of planets in epicycles? They’re very different!
Glad you asked. Yes, these were two different – completely different – ways to model the solar system motions. The way that people (uneasily?) managed is that the model of Aristotle was how things really were. The model of Ptolemy was just a calculator…to make predictions without expecting that the planets actually moved in the way his model pictures.
What Ptolemy believed, is precisely what everyone believed: orbits of the extraterrestrial objects were circular18 and that the Earth was the center of the Universe and all of the planets and stars moved around it.
9.5.4 Aristarchus
Was everyone on board? There had been other models of the solar system, most memorably by Aristarchus of Samos (310 BCE - 230 BCE) (Samos is an island just to the west of modern Turkey) who lived during the time of Archimedes, who commented on his work. Aristarchus proposed that the Sun was the center of the Universe and that the Earth and all of the planets revolved around it. This idea had also been put forward as a logical possibility before even Plato’s time. But Aristotle insisted that the Earth could not possibly move since when an arrow is shot directly overhead it should land behind the archer since the Earth would have moved out from underneath. Or if the Earth moved, then it would leave its atmosphere behind.
🖋 📓
The more serious problem with an Earth revolving around the Sun can be tested while you’re reading this. Look across your room and close one eye, take note of where something in your foreground is relative to the far wall and then close the other eye and open the first. Go back and forth and you’ll see that the foreground object seems to hop from left to right depending on which eye you’re looking through. This phenomenon of your binocular vision is called parallax.
If your left eye plays the role of some hypothetical postion of the Earth and your nose is the Sun, then your other eye is the position of the Earth six months later, on the other side of the Sun. Nobody saw the presumably fixed stars appearing to move relative to the Earth at those extreme positions…so they concluded that the Earth is not moving. Or so the argument went, since for there to be no parallax the Universe would have to be so large as to be beyond comprehension. That was Archimedes’ argument: the Universe cannot possibly be so large! It was not until the 1838 that measurements could be made with telescopes precisely enough to confirm stellar parallax and hence the first demonstration that the Earth indeed moves around the sun. But Aristarchus had a fan.
📺
You might benefit from 5.2_cosmology1_q_v1.mp4 for review and wrap-up of these sections.
{: .dealclass}
9.6 Putting the Sun Where It (almost) Belongs: Copernicus
🖥️
Please answer Question 2 for points: who said that?
🖥️
Please answer Question 3 for points: Why did Greeks reject it?
🖥️
Please answer Question 4 for points: Ptolemy did what?
The Renaissance and the rise of humanism brought with them a freedom of thinking. Universities began to flourish, especially in Italy, Paris, and Oxford. A century before Galileo joined the faculty at Padua, an unassuming Pole also went to Padua to study medicine, for which it was particularly renowned, but similarly to Galileo, he couldn’t shake his fascination for mathematics and astronomy. Nicolaus Copernicus (1473-1543) was sent to Italy by his uncle who was the Bishop of Warmia to study canon law at Bologna but he actually studied in Padua, Rome, Bologna, and Ferrara. While in Bologna, he lived with the faculty astronomer and made many observations with him. (The primary job of a late medieval astronomy professor included teaching mathematics and astrology.) He eventually went on to Padua to study medicine and believe it or not, astrology was an important tool for doctors and so Copernicus was well-prepared. While he obviously had trouble “declaring a major” he did manage to receive his canon law doctorate degree and have sufficient training in medicine that he would be a practicing physician and personal assistant to his uncle for the rest of his benefactor’s life.

Figure 9.10: The late 1500’s saw the publication of a corrected version of Almagest by Johann Müller, known as Regiomontanus in 1497. This Epitome of Ptolemy’s Almagest was the textbook would have been familiar to every astronomer of the 15th century.
His uncle set him up with a local academic appointment, but with the stipulation that he never needed to appear on campus! He was solely detailed to tending to his uncle and as a canon19 with minimal bishopric duties.
Copernicus never took vows and so was a lifelong lay-clergyman. He took a mistress and his hobby: was astronomy. He had learned Greek in Italy and slowly began to question the Aristotelian and Ptolemaic pictures, being especially irritated with Ptolemy’s use of the equant, believing that it destroyed the symmetry. He knew of Aristarcus and began to think differently.
What intrigued him was that the order of the planets was arbitrary in the Ptolemaic system—he thought there should be some correlation of motion with the positions of the planets. In the figure above depicting the Aristotelean universe the planets ordering was Moon, Mercury, Venus, Sun, Mars, Saturn, Jupiter, and the stars. Sometimes people put Venus closer to Earth. What he knew however was that the years of each planet were ordered and perhaps the Humanist fascination with the Sun rubbed off on him a little. In any case, he made a stab at suggesting a Sun-centered picture with the planets in the order that we know them now, following the lengths of the years of each as one gets further away from the Sun. His little attempt was written some time before 1514 and distributed to friends and called Nicolai Copernici de hypothesibus motuum caelestium a se constitutis commentariolus, a “little commentary,” or Commentariolus. In it he lays out his plans in about 40 pages, but not logic. It made it to Rome and and it’s known that Pope Clement VII heard a lecture on it 20 years after its production and was intrigued. It listed Copernicus’ objections and a set of assumptions: basically, the Sun is stationary, the Earth moves around it annually, the Earth rotates on its own axis daily, and that retrograde motion is a natural consequence of the relative orbit of Earth and the other planets.

Figure 9.12: On the left is the medieval tower in cold, marshy northern Frauenburg on the Baltic Sea in Prussia (Poland) where Copernicus wrote his famous book. On the right is the picture that everyone thinks of when they think “Copernicus”…except it’s not quite so simple.
This went okay and high ranking clergy even offered to support him in the production of a more complete book. But there was enough criticism and it seems that Copernicus had thin skin and he waited almost 40 years to write the complete story: De revolutionibus orbium celestium (On the Revolutions of the Celestial Orbs (orbits)…the densest treatise on spherical geometry, maybe ever.
He came to produce Revolutionibus somewhat reluctantly. It took decades. It seems he required an odd companion.
9.7 Revolutionibus and Scandal
9.7.1 The Copernican System
In school you probably learned of the Copernican system of the planets. The Sun in the center of the solar system and the planets all orbiting in perfectly circular orbits. The right-hand figure above is familiar and indeed an image from Revolutionibus. In it, he criticizes the Ptolemaic system as a Frankenstein monster of sorts:
“…the true symmetry of its parts…they have been like someone attempting a portrait by assembling hands, feet, a head and other parts from different sources. These several bits may be well depicted, but they do not fit together to make up a single body. Bearing no genuine relationship to each other, these fragments, joined together, produce a monster rather than a man.” To him, there was no alternative than to order the planets according to the length of their years. “Thus we discover in this orderly arrangement the marvelous symmetry of the universe and a firm harmonious connection between the motion and the size of the spheres….”
Finally, the Sun, rather than just another orbiting bit takes on a central role:
“Behold, in the middle of the universe resides the Sun. For who, in this most beautiful Temple, would set this lamp in another or a better place, whence to illumine all things at once? For aptly indeed do some call him the lantern – and others the visible god, and Sophocles’ Electra, the Watcher of all things. Truly indeed does the Sun, as if seated upon a royal throne, govern his family of planets as they circle about him.”
Circles. Always circles.
Wait. We all learned that the orbits of the planets are not perfect circles, but the orbits are elliptical in shape. How did Copernicus get away with circles?
Glad you asked. He couldn’t! In fact, he required the use of epicyles as well as Ptolemy. His were not around deferents that went around the Earth, but rather the Sun. But clearly, he could not make circles work by themselves.
🖋 📓
But Copernicus needed help with his circles and that came in the form of as many epicycles as Ptolemy!
Was Copernicus afraid of the Church? Not really. Remember, he had supporters and he was respected in the Vatican. He dedicated Revolutionibus to Pope Paul III! Things got bad for Copernicus’ work long after he had left the scene…and after the Vatican home-office decided to reboot and reassert its dominance in opposition to Protestantism and the general corruption of its far-flung clerical satellite offices.
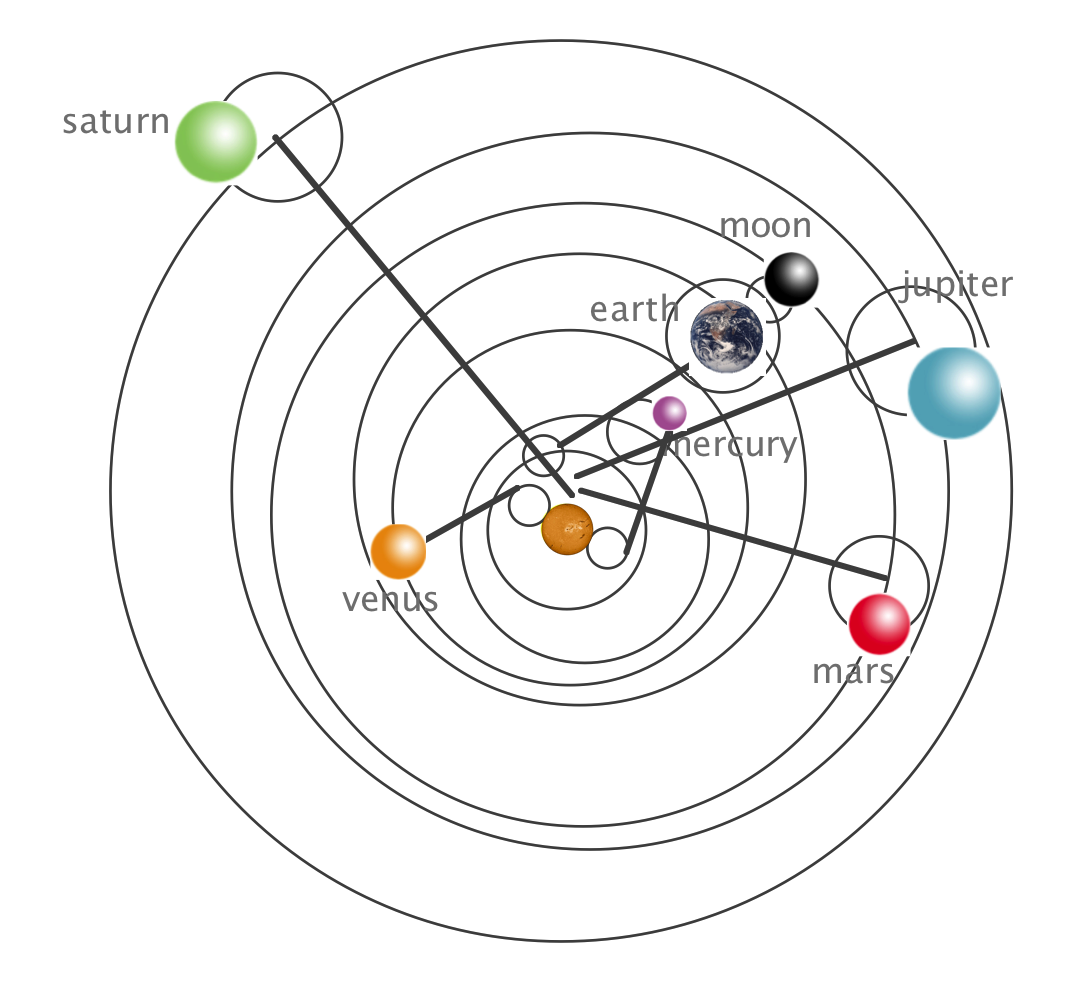
Figure 9.13: A rendering of Copernicus’ actual calculational model. Many epicycles, now to mimic elliptical motion, not to solve the retro- grade motion problem
When he finished the work, his assistant had to leave to go back to his home university. He took the manuscript with him, intending to drop it off at the publisher in Nürnberg, but left oversight with another Lutheran minister, Andreas Osiander, a dabbler in mathematics and familiar with this kind of publishing.
Protestant Osiander had been in communication with Copernicus and urged him to not state that the world was the way he presented it, but that his work was just a hypothesis. Catholic Copernicus ignored that advice. But Osiander did Copernicus a dirty trick. He added a preface of his own construction, which was a scandal:
“Since [the astronomer] cannot in any way attain true causes, he will adopt whatever suppositions enable the motions to be calculated…. For hypotheses need not be true nor even probable. On the contrary, if they provide calculations consistent with the observations, that alone is enough…. Different hypotheses are sometimes offered for one and the same motion (for example, either an eccentric or an epicycle model will explain the Sun’s motion). The astronomer will adopt whichever hypothesis is easier to grasp…. So as far as hypotheses are concerned, let no one expect anything certain from astronomy… lest he accept as truth ideas conceived for another purpose, and depart from this study a greater fool than when he entered it.”
Copernicus surely didn’t know that this had been added to his book as he’d suffered a debilitating stroke and died at the age of 70 on May 24, 1543. The touching legend is that he was presented with the published version on his deathbed, but that’s unsubstantiated.
Where he was buried was a mystery until 2008 when archaeologists found a skeleton under the Frombork Cathedral floor. DNA from grave matched DNA from hair found in a book that Copernicus owned. He was given another funeral in 2010 in the Cathedral, where his grave is now adorned with a handsome replica of the idealized Solar System as we know it today.
Copernicus came along at the right time and in the right place to re-imagine the planets in orbit around the Sun. His arguments were not driven by data – his model wasn’t more accurate than Ptolemy’s. Rather his argument was basically one of symmetry and philosophy. He thought that Ptolemy had described an ugly circumstance and could not explain the order of the planets.
The planets of our solar system orbit the sun.
🖥️
Please answer Question 5 for points: Copernican system accuracy
📺
You might benefit from 6.1_cosmology2_copernicus_v1_.mp4 for review and wrap-up of these sections.
{: .dealclass}
9.8 Astronomy, If It Ain’t Baroque, Don’t Fix It: Tycho
Not much notice was taken of Copernicus’ work. The most dismissive was Martin Luther, as the new Protestantism was literal in Biblical interpretation. Copernicus’ work was taught in a few places, but mostly “after school” by individuals who might lecture on the standard Aristotelian model during the day, but privately instruct students off-hours. One such instructor was Michael Maestlin at the University of Tübingen. He taught Ptolemy and Copernicus and one of his avid pupils was the young Johannes Kepler who became a Copernican as a result. He was studying for the ministry, but his mathematical skills were unusually advanced and upon graduation he was recommended for a position as mathematics instructor Protestant school in Graz, which he accepted.
As we’ve seen, Kepler was an amazing specimen, but physically and emotionally…a wreck…all of his life. He was an extreme Platonist, or even Pythagorean. This means that he believed deeply that the universe was governed by perfect mathematics – that the universe actually is mathematics – and this fit his deeply religious, almost mystical inclinations. His devotion to the curious model of the Platonic solids and their seeming relationship to the planets’ orbits made perfect sense to him. A believer in the reality of math.
He worked for various bigger-than-life people in Germany, Austria, and Czechoslovakia. His first big employer was the very unusual, Tycho Brahe.
9.8.1 The First Laboratory Director: Tycho Brahe
The Dane Tycho Brahe (1546 - 1601) was, like Copernicus, another nephew of a powerful man who directed his education. However, unlike Copernicus who’s father had died, Tycho’s uncle actually kidnapped him to raise as his own. Tycho was not exactly a shy guy. Yes, the famous nose story is true: he was sent to the University of Copenhagen and as a 20 year old got into an argument over mathematics which led to swords, and he lost the tip of his nose. Because everyone defends mathematics to the death. For his entire life he famously wore a nose made of metal – gold, silver, brass – that he would attach with glue. He’d be talking, his nose would fall off…and he’d reattach it like it was a normal thing. Well there was nothing normal about Tycho. You can just make out this odd attachment in his portrait.20
Tycho had become a particularly astute observer of the positions of the stars and planets and even though his uncle wanted a lawyer, he was fascinated by astronomy. His uncle died and then his father, and another uncle helped him to build an astronomical observatory. This family was extraordinarily wealthy.
9.8.2 Shattering the Crystaline Spheres
On November 11, 1572 he observed a new star in the constellation Cassiopeia. This object was so bright that it would shine during the day, which must have been unnerving. By this point in his development he was an expert observer and by measuring positions carefully he determined that there was no parallax, and that hence this nova stella (new star) was far outside of the Moon’s orbit, and likely with the distant stars. His designation of “new star” is how we get our name “supernovae” and the event that he witnessed, and wrote about in a popular book, is called now Tycho’s Supernova, or in astrophysics-geek-speak: SN 1572. The figure below on the left is from his book, De nova stella.

Figure 9.15: On the left is Tycho’s Supernova as he drew it in his publication. It’s the star labeled “I” in the constellation Cassiopeia. On the right is the image of the remnant today as observed by the orbiting Chandra X-ray telescope. (Only very powerful optical telescopes can see it now.) The blue edge is X-rays emitted from a very hot shock wave that’s still expanding at a ferocious rate. The red are lower energy X-rays. It’s about 55 light-years across and 13,000 light years from Earth. This is a Type Ia supernova which will become an important class of exploding star when we study 21st century cosmology.
With this observation the cracks began to form in Aristotle’s model that the planets and stars were firmly attached to real, rotating, crystalline, Earth-centered spheres. Here’s the first problem for Aristotle for which evidence suggested otherwise.
This analysis vaulted Tycho into celebrity status in Europe as a result of his dramatic explanation. The heavens were not permanent! He further observed a comet and showed that it too had to be outside of the Moon’s orbit. One of the absolute certainties in Aristotle’s cosmos was that every celestial object beyond the Moon was permanent. Tycho had demonstrated convincingly that this couldn’t be true since a new star was born, literally before everyone’s eyes.
The King of Sweden, fearing losing him to another country, gave him the island of Hven in Oresund. And built him a laboratory in 1576 that was unlike anything since Alexandria. Tycho inherited not only the land, but the people who lived on the island. Uraniborg was a complete national laboratory. It had more than a hundred lab assistants, carpenters, machinists, gardeners, a police force, a printing office, and the best instruments in the world. And there for the next 23 years, every night, he and his assistants recorded the positions of 1000’s of stars and full orbit positions for all of the planets over two decades. And, he came up with a model of the solar system that was Copernican, but not Copernican.

Figure 9.16: Breaking News: A rendition of the 1577 comet.
🖋 📓
The next shoe to drop was the Great Comet of 1577. Tycho again made meticulous measurements and found a number of startling things. First, the comet seemed to be related to the Sun—its tail always pointed away from it. Second, it was also clearly outside of the Moon’s orbit among the planets themselves with an apparently varying speed. Somehow this object pierced the crystalline spheres – without any effect in its motion – while following a new circular path. Maybe those fanciful planet-carriers didn’t exist?
“Now it is quite clear to me that there are no solid spheres in the heavens, and those that have been devised by authors to save the appearances, exist only in their imagination, for the purpose of permitting the mind to conceive the motion which the heavenly bodies trace in their courses.”
He had a model.
The cosmos changes and is not perfect.
and the comet observation and measurements show that
Aristotle’s model of crystalline spheres could not be correct.
The Tychonic “System of the World” was a clever way to solve some of the problems that Copernicus’ system also solved. In his picture, shown here:
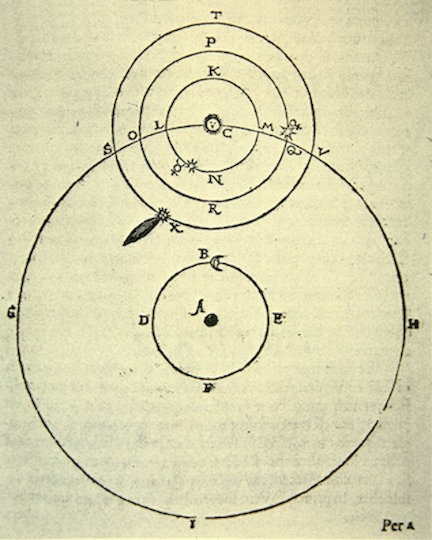
Figure 9.17: Tycho’s model of the solar system is geometrically the same as Copernicus’ but has the Earth still while the Sun orbits it with all of the planets then orbiting the Sun. (Notice the comet in its own little Sun-centered orbit). Note: No crystalline spheres here.
His thinking was that the Earth is too ponderous to move and so it’s indeed stationary with the Sun and the Moon orbiting around it in a circle. All of the other planets then revolve around the Sun. This way Mercury’s and Venus’ relationship to the Sun was fixed and likewise retrograde motion was also accounted for and the changing brightness of Venus is solved. His objection to Copernicus was both scientific and religious. He was able to determine from measurement that if the Earth were orbiting the Sun that the lack of retrograde motion required the stars to be more than 700 times the distance to Saturn. While a long way, he was not motivated just by the sheer magnitude of that distance, but the fact that the stars appear to have a size and that size could not be so bright if they were that far away. Now of course the stars do have a size, but not that we can see from Earth. Optical effects give the impression that they are extended. Notice how the crystalline sphere idea can’t work in his model. They’d overlap and crush one another.
Tycho’s was a legitimate competitor with the Copernican model until stellar parallax was definitively observed in the 19th century. The Catholic Church loved it as we’ll see. But that wasn’t enough to save Uraniborg. The new King of Denmark would not sustain funding for his lab – which was costing about 1% of the entire national budget – and so Tycho had to move. His entire menagerie, including his pet moose, moved to Prague where he became the Imperial Mathematician to the Holy Roman Emperor, Rudolf II. Yes, the Lutheran Tycho was employed by the Roman Catholic Emperor. Tycho’s moose drank too much beer and died falling down some stairs and Tycho drank too much at a state dinner and because of protocol would not leave the table. Later his bladder burst and he died painfully in 1601. And then a fight broke out.
📺
You might benefit from 7.1_cosmology3_tycho_v2.mp4 for review and wrap-up of these sections.
{: .dealclass}
9.9 Kepler’s Battle With Mars
When Kepler went to work for Tycho in Prague it turned out to not be a marriage made in heaven. Kepler inherited Tycho’s job as Imperial Mathematician and a long headache of law suits. Tycho was possessive of his data and Kepler wanted desperately to get his hands on it and was frustrated at it being fed to him piecemeal. He was determined to solve “the Mars problem,” namely the retrograde motion problem and Tycho’s decades of precise Mars data was just out of his grasp. However, Tycho’s mishap at the banquet left Kepler with an opportunity, which he took. Or rather, he took the data, only to be hounded by Tycho’s heirs for nearly the rest of his life. In a legal decision, he agreed to publish Tycho’s data in a book dedicated to the Emperor and the Rudolphine Tables were eventually published, but not until Kepler had thoroughly analyzed the data. He won the battle of Mars.
🖋 📓
Remember that circles were an unquestioned feature of all of astronomy for two millennia. What Kepler found was that the orbit of Mars would just not fit a circular path. After anguishing over this, in heroic calculations, he determined that the orbit was elliptical with the Sun, not at the center of the ellipse, but at one of the foci. This was an intellectually brave conclusion given the dominance of the circular prejudice. In 1609 he published these ellipse results (Kepler’s First law) in Astronomia nova (New Astronomy) along with his discovery that the planets sweep out equal areas in equal times as their speeds change as the approach and move away from the Sun (Kepler’s Second Law, but it actually came first). Notice in the figure that the area A is equal to area B, so that the planet is going faster close to the sun.
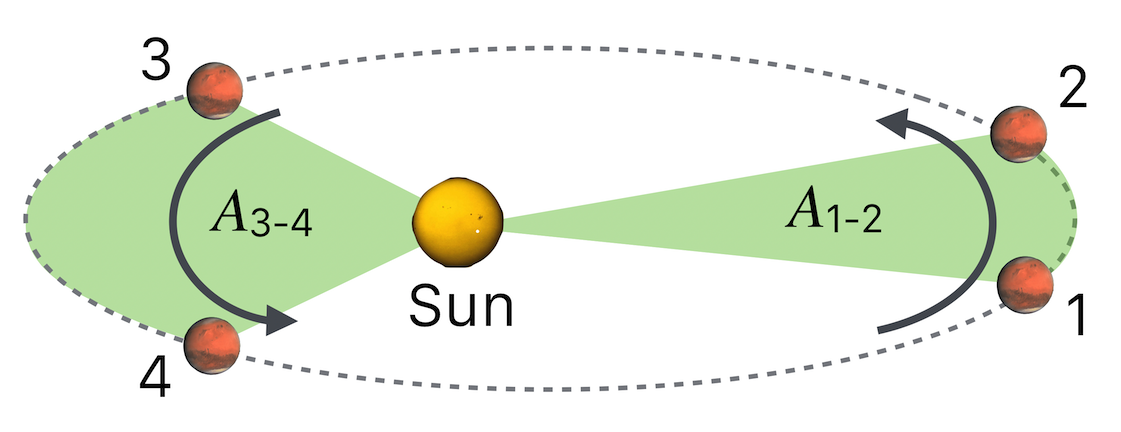
Figure 9.18: Four instances of Mars in its orbit around the sun. Note that this is highly exaggerated! The time that it takes for Mars to go from position 1 to position 2 is the same as to go from position 3 to position 4. Think of each slice of time to be a “Mars month,” (which makes no sense since Mars doesn’t have a moon, but you get the point). During each of these equal intervals, notice that the path that Mars sweeps out is much different at its farthest from the Sun (1-2) than the path closest (3-4). Keplers Second law says that the areas that are swept out by the planet (\(A_{1-2}\) are equal: \(A_{1-2} = A_{3-4}\)
The planetary orbits are in the shapes of ellipses.
Later in 1619 he published an extension of his cosmology in Harmonices mundi libri, Harmonies of the World. Plato’s solids were still there as was a considerable amount of new mathematics, and his Third Law: for any two planets the ratio of the squares of their periods21 is proportional to the ratio of the cubes of their average distance from center of their orbits. Said in symbols, where \(T\) is the period and \(R\) is the mean orbit radius:
🖋 📓
\[\begin{equation} T^2 \propto R^3 \tag{9.1} \end{equation}\]
This can be turned around into an equation by creating a constant of proportionality, \(k_S\), for “sun.” Then:
\[ \begin{equation} k_S = \frac{T^2}{R^3}. \tag{9.2} \end{equation} \]
Using modern numbers for a few of the planets:
| planet | period (s) | average distance (m) | \(k_S\) |
|---|---|---|---|
| earth | \(3.156 \times 10^7\) | \(1.4957 \times 10^{11}\) | \(2.977 \times 10^{-19}\) |
| mars | \(5.93 \times 10^7\) | \(2.278 \times 10^{11}\) | \(2.975 \times 10^{-19}\) |
| saturn | \(9.27 \times 10^8\) | \(1.427 \times 10^{12}\) | \(2.957 \times 10^{-19}\) |
Notice that they all have the same value for \({T^2}/{R^3}\), what I’ve called \(k_S\). This agreement is universal for all of the planets…and as we’ll see, any “Copernican-like” system. Such as the moon-earth? Stay tuned.
All told, he proposed 3 rules, which of course are called Kepler’s laws:
- The law of Orbits: All planets move in elliptical orbits with the sun at one focus.
- The law of Areas: A line that connects a planet to the sun sweeps out equal areas in equal times. You can see this in the figure above. Notice that this requires that when a planet is near the sun it’s moving faster than when it is away from the sun.
- The law of Periods: The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit. This is written just above in a simple proportionality. The planets are truly elliptical, but not very much so that \(R\) can be treated as the average radius of the orbit with little error.
Kepler was quite amazing. While considerably under pressure of family and health he came close to inventing calculus (in trying to calculate the volume of wine casks), conceiving of gravitational attraction as the source of planetary binding (he was familiar with the work of Walter Gilbert in England who determined that the Earth was a large magnet and imagined the Sun as emanating a magnetic attraction to the planets), optical telescopes (he worked out the correct geometrical optics of concave and convex lenses after Galileo’s publications), and fiction (as I mentioned, he wrote the first science fiction novel).
📺
You might benefit from 7.2_cosmology3_kepler_v3.mp4 for review and wrap-up of these sections.
{: .dealclass}
Kepler is one of my personal scientific heroes. He, before anyone, was intellectually brave enough to abandon circles as the path of the planets. He followed the data, rather than authority.
In some ways, he straddles the Renaissance and the birth of modern physics and astronomy. So in the next chapter we’ll take the leap into the Scientific Revolution with Galileo’s telescope and Newton’s enormous intellect.
🖥️
Please answer Question 6 for points: getting off the bandwagon
🖥️
Please answer Question 7 for points: speed near the sun
🖥️
Please answer Question 8 for points: comparing planets
🖥️
Please answer Question 9 for points: and again, but different
🖥️
Please answer Question 10 for points: ranking our astronomers
9.10 What to Remember from Lesson 9?
There is much misunderstanding of the history of early cosmology up to just before Galileo (whom we’ll revisit in the next lesson). Here are some takeaways that speak to some of the legends.
- There were Greeks who proposed models (we talked about one) in which the Sun was at the center of the solar system. These models were rejected for perfectly sane empirical reasons.
- The “crystaline spheres” model of Aristotle, and hence all of the West up to the Baroque period was not compatible with the epicyles model of Ptolemy. In fact almost nobody believed that there were real epicycles, rather that the Aristotelian picture was how things really were. But if you were a doctor and needed to predict the motions of the planets, Ptolemy’s model gave you correct answers. It’s really remarkably contradictory!
- The picture of the solar system that’s taught to every child and credited to Copernicus of all of the planets moving in circles around the Sun is not what Copernicus’ model actually said. It couldn’t have been his model since we know that the orbits are elliptical, not circluar. So Copernicus would get the wrong answer. He knew that, so he built in his own system of epicycles – as many as Ptolemy – so that his model would predict planet positions correctly. It was no more accurate than Ptolemy’s and so everyone pretty much kept using the Egyptian’s model, not the Pole’s.
- Kepler is a true intellectual hero in the history of science. Not one person conceived of the orbits being other than circular. They look circular. Circles matched a preconception of the perfection of the heavens. But Kepler all alone proposed that this was wrong.
Kepler’s three laws are essential to an appreciation of a more modern view of planetary science.
- His First law: the planets travel in elliptical orbits around the Sun, which is positioned at one of the foci of the ellipse.
- His Second law: The speeds of the planets in their orbits are not constant. They move faster near the Sun than away from the Sun. What is constant for their orbits is that in the same amount of time, a planet always “sweeps” out the same area between it’s orbit and the Sun.
- His Third law: in words…The square of the period (the time to complete one orbit) of a planet is proportional to the cube of the mean distance of the planet from the Sun. This proportionality is written as an equation:
\[ \begin{align*} T^2 &= k_S R^3 \\ k_S &= \frac{T^2}{R^3} \end{align*} \]
The constant of proportionality is explicitly written with the subscript “S” since it refers to orbits around the Sun. Anything– a planet, an asteroid, an artificial satellite – that’s gravitationally bound (using a Lesson 9 phrase!) to the Sun obeys precisely this relationship with the same value for \(k_S\) as the planets.
Kepler went very close to imagining a force created by the Sun to cause this almost-circular motion to take place. He called what we refer to as a force, a “soul.” He also assumed that there must be another forcee that points along the trajectory, which we know is not required or possible in circular or any non-straight motion. He anticipated Newton in many ways.
Marishal College was merged with another university and Maxwell was deemed “redundant” because there is only one “professor” in any subject.↩
This is completely arbitrary! The North Star – Polaris – just happens to be near the apparent axis around which the stars are traveling in a night. During the time of the Greeks, there was a different star and later, no star. This is because the Earth’s spin is actually precessing – wobbling like a top – and over long times things like this happen. Enjoy Polaris’ useful spot while it’s available!↩
Remember, he insisted that all Earthy matter would head for the center of the Universe, which was the center of Earth. So from all directions, the built-up mass that is our terra firma, would create a sphere. Also it was well-known that the Moon shines because of the Sun’s light and the phases of the Moon were a reflection how the Moon was oriented towards the Sun. So nobody of Greek influence believed that the Earth was flat.↩
although he clearly had to do some strange things to preserve circles!↩
Which is a secular position.↩
Recent exhumation and analysis suggests that the nose was brass. Legend suggested precious metals. Oh well.↩
The Period is the time that it takes for any repeating motion to come back to its starting point. So the period of the Earth’s orbit is one year.↩