Lesson 6 The Big Mo, Force and Momentum
6.1 Contents
- A Little Bit of Newton
- Impulse
- Newton’s Mass
- The “Quantity of Motion”: Momentum
- Newton’s Famous Three laws
- Newton’s Second law
- Weight
- Finally, Nothing: Forces in Balance
- Circular Motion
- What to Remember from Lesson 6?
6.2 Goals of this lesson:
- I’d like you to Understand:
- How to calculate a force required to produce a particular acceleration in one dimension.
- How to calculate the average change in momentum induced by the application of a force through a finite period of time.
- How to calculate the centripetal force and acceleration for an object moving at a constant, circular speed.
- I’d like you to Appreciate:
- Forces create accelerations.
- That if a momentum vector is changing in direction or magnitude, a force is the cause.
- That an object moving in a curved path must have had a force applied to it perpendicular to the trajectory.
- I’d like you to become Familiar With:
- Newton’s third law
- Newton’s Life
6.3 A Little Bit of Newton
I’m always saddened when I think of this young man’s childhood. Imagine a 3 year old abandoned by his newly-married mother and forced to live with grandparents who didn’t want him. That’s the beginning of the biggest scientific life of all: Isaac Newton’s. His childhood was a mixture of pain and some accidental fortunate associations. His father was a farmer in Woolsthorpe, not far from Nottingham and a little more than 100 miles north of London. Isaac senior died before tiny, premature Isaac was born. When he was 3 years old, his mother, Hannah—a semi-literate woman for whom the farm and manor was a big job—married the 63 year old Rector of North Witham who wanted nothing to do with a frail toddler who was then left in the care of his maternal grandparents and female cousins. Seven years later, Hannah, a widow yet again, returned with two young children in tow. While she had been away, young Isaac had been sent to school, a privilege that might not have happened had his father been alive. He’d have become a farmer. But a bad one.
When he was 12 years old, Isaac was sent to a Free Grammar School in Grantham where the emphasis was Latin (“Grammar,” after all), which was the language of intellectuals and in which he wrote his great works. He lived with the apothecary, another lucky break as that family indulged his precocious abilities with tools and crafts. In what must have been one of the most frivolous activities of not just his adolescence, but his entire odd life, one night he constructed dozens of kites with firecrackers, which he flew over the town at night “…wonderfully affrighting all of the neighboring inhabitants for some time, and causing not a little discourse on market days…”
He was a loner then, and for most of his adult life. “His school fellows generally were not very affectionate toward him. He was commonly too cunning for them in everything. He who has most understanding is least regarded.” When he was 17 years old Hannah tried to turn him into a farmer, but he was a disaster. She gave up and sent him back to Grantham to prepare him for university…as the only outlet for his increasingly apparent, unusual mind.
He was sent to Trinity College at Cambridge University where he was enrolled as a “Sizar,” which was essentially the role of servant to an upperclassman. He was 18 years old, older than most of the students and as a studious person, different from the mostly carefree student body. He made a single friend, a most unlikely event for the difficult Newton. One day he met a fellow lonely student on a park bench. John Wickins and Isaac Newton found commomn interests and became roommates—for 20 years until Wickins married. Wickins was Newton’s assistant as he began his life of changing the world.
The curriculum at Cambridge was reliably old-fashioned: Aristotle, from top to bottom. But René Descartes from the Continent was all the rage and was read and secretly discussed by students. To Descartes, the world was mathematical in a manner beyond what Galileo might have imagined. It was he who blended geometry together with the brand new algebra so that equations could be presented as curves and equivalently, curves as equations. Of course we call our axes, “Cartesian” after their inventor.
Descartes was also a mechanist: meaning he believed that matter’s mechanical interactions caused all motion. Nothing spiritual, nothing occult, nothing random. God originally inserted overall motion into the universe, and apparently then abandoned his creation in order to pursue other interests? In any case, Descartes believed that original motion persisted as the universe formed and that God did not drop in and adjust things. Even the planets moved by being carried by vortices of invisible spheres. His world was predictable according to Laws (yes, capital L for Descartes’s purposes), and he proposed to start with them and draw observable conclusions—deductions. Mechanical modeling was his goal, and analytical mathematics was his tool. Very top-down was Descartes: postulate the principle idea and causes and draw conclusions deductively. Without that original cause, the conclusions can’t happen. Always: the causes of things had to come first.
Descartes was all about Why. Newton weaned us from Why to How.
The young, inquisitive Newton ate Descartes up. Here was an escape from Aristotle and a systematic and mathematical way out—right up Newton’s alley. But Descartes’ conclusions and his method were problematic for Newton and much of what he later wrote was in reaction to this unrequited disagreement.
But the Frenchman’s mathematics stuck and the neo-Platonists at Cambridge carried Descartes’ mathematics program forward. The leader of that movement was Isaac Barrow, the first “Lucasian Professor of Mathematics.” Isaac Newton was the second (Paul Dirac, who we’ll meet later, was 15th and Stephen Hawking was the 17th). Newton became a student of Barrow’s and eventually his beneficiary.
Disaster struck in London 1664 when the Bubonic Plague raged Before it was over, 20% of the population was dead. By 1665 London emptied out (one imagines frightened servant staff remaining behind to protect their masters’ homes while the families fled). Cambridge University closed and the 23 year old Newton went home to Woolsthorpe, where he worked by himself for more than a year. During that period he consumed all mathematics known at the time and went beyond. While at the farm, he essentially invented calculus, had his first ideas about gravity (the famous apple was to have fallen in his presence during this period), and reinvented the science of optics.
What did you do on your summer vacation?
“In the beginning of the year 1665 I found the Method of approximating series & the Rule for reducing any dignity of any Binomial into such a series. The same year in May I found the method of Tangents…, & in November had the direct method of fluxions & the next year in January had the Theory of Colors & in May following I had entrance into the inverse method of fluxions. And the same year I began to think of gravity extending to the orb of the Moon & (having found out how to estimate the force with which a globe revolving within a sphere presses the surface of the sphere) from Kepler’s rule…I deducted that the forces which keep the Planets in their Orbs must be reciprocally as the squares of their distances from the centers about which they revolve: & thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the earth, & found them answer pretty nearly. All this was in the two plague years of 1665 & 1666. For in those days, I was in the prime of my age for invention & minded Mathematicks & Philosophy more than at any time since.”
Among Newton’s discoveries during the plague years was that sunlight is composed of all colors, which was in conflict with the standard (Cartesian!) idea that white light was a color of its own and that the colors we see are mixtures of white and dark. He passed light through a prism and found that it spread out into a continuous spectrum of colors. This led him to experiment with light passing through glass and to grinding his own lenses for telescopes. Telescopes had become long and unwieldy and because glass lenses spread out the colors (“chromatic aberration”) precise images were difficult to achieve. Newton changed the design completely, using mirrors rather than lenses. The result was images of higher quality with higher magnification in a compact instrument. His original six-inch “Newtonian reflecting telescope” would magnify 40 times, which would have required a six-foot long conventional telescope resulting in a poorer image to boot. All telescopes today are off-shoots of the Newtonian design.
When he returned to Cambridge his mathematical skills exploded, surpassing those of all around him. In 1667 at the age of 25 he was named a Fellow (like an assistant professor) with a salary. In 1669, Barrow resigned the Lucasian Chair insisting on Newton’s appointment to this highest post in the college. (“Mr. Newton, a fellow of our College, and very young … but of an extraordinary genius and proficiency in these things.”) One of the few duties of the Lucasian Chair was to offer a single course a year, which he dutifully fulfilled, but often lecturing to an empty classroom since nobody could understand him.
The reflecting telescope and his explanation constituted his first entry toward membership in the Royal Academy of Sciences. His report on how it worked led to the explication of his theory of light, which the Curator of Experiments, Robert Hooke, thought was stolen from his (incorrect) ideas. They became bitter enemies for life, one of a number of such vicious rivalries that Newton suffered into—and beyond—old age.
So galling was this dispute and the criticism that his theory of colors attracted from all over Europe, that Newton went into nearly complete isolation, vowing to keep the products of his research secret, rather than ever again suffer such public antagonism. He communicated almost exclusively through voluminous correspondence, much of which still exists. Newton didn’t suffer fools well, and even a legitimate dispute would send him into a towering rage, or stony silence. His response to Hooke was to write a book on optics, which he inadvertently destroyed when a fire from an alchemy experiment went out of control. (He rewrote it many years later.)
That’s not all
Newton was an accomplished alchemist, damaging himself with the noxious chemicals that he inhaled and tasted. He had strange ideas about non-scientific things. For example, he believed that God had given first-knowledge of the physical universe to the Ancients (which they suppressed…whoever “they” were), and that among those ideas were alchemical discoveries still to be found. His lodging was near to his laboratory on the Cambridge Trinity College campus and a huge furnace fire was never put out as he single-mindedly attacked alchemy, the precursor to chemistry.
He also was an unusual religious fanatic. He learned Hebrew and translated the Bible from original texts and became convinced that fourth-century changes made the false claim of the divinity of Jesus. So he was a very un-traditional Christian, a believer in a God of Nature, but not the Trinity. He wrote much more about alchemy and his heretical religious research (unrevealed until after his death) than he did about science!
What we recognize as Newton’s enduring scientific work came as the result of a wager, and we’ll pick up that story when we study his law of Gravitation and the first-ever attempt at a scientific cosmology in our lesson on Gravitation. Everything he discovered about mechanics and gravitation is contained in one enormous, ponderously written, thickly Latin, often revised book.
The Book
Newton was in his 40’s when he basically sequestered himself in his rooms, working on his alchemy and intensely strange religious researches. In 1684 three of his colleagues the famous London architect Christopher Wren, the scientist Edmund Halley (of eventual comet-fame), and his arch nemesis Robert Hooke were trying hard to figure out the shape of a planetary orbit if the force of gravity varied like the inverse square of the distance from the Sun. Hooke claimed in his obnoxious way that he knew the answer, but he would not produce a calculation—because he couldn’t: he had no mathematical training. He prospered entirely on his remarkable instincts as an experimenter.
But, a little of Robert Hooke went a long way, and Wren and Halley got tired of listening to him so they deputized Halley to go ask Newton. He showed up unannounced at Newton’s messy room and asked him. Immediately came the recluse’s famous response: “An ellipse.” “Why?” asked Halley. “Because I have calculated it.” But, typical of the paranoid Newton, he’d not told anyone.
He’d worked out the mathematical rules for the motion of the planets and kept it a secret! While Halley waited, Newton searched but could not find his calculation, and Halley left empty-handed. A few days later, Halley received nine pages from Newton that showed: if the force on a planet varies like the inverse square of the distance from the center of the orbit at the Sun, then the orbit’s shape must be a conic (a parabola, ellipse, circle, or hyperbola). And he showed that if the orbit is an ellipse, that the force of attraction must be an inverse-square. This pamphlet became known as, De Motu Corporum in Gyrum (On the Motion of Revolving Bodies). De Motu, as it’s known, was a summary of the first book of his eventually triumphant work. The figure at the side shows a page of De Motu in Newton’s hand that he later prepared for his correspondent-friend, John Locke. This electrified Cambridge and London and set Hooke’s teeth on edge as he’d guessed some of the same conclusions and again insisted that Newton had stolen his ideas.
Halley realized what Newton had done and implored him repeatedly to write it all. Newton finally agreed and went into one of the historically most intense periods of concentration ever embarked on by anyone. For two years he worked night and day, forgetting to eat, wandering around Cambridge without regard to his surroundings. Thousands of pages of manuscript littering his quarters mingled with days’ worth of uneaten food. Two years! Eventually he emerged with the first book of what was to be three volumes of Philosophicæ Naturalis Principia Mathematica, or the Mathematical Principles of Natural Philosophy affectionately known ever after as The “Principia.” It was all there in Latin. His laws of motion and gravitation, but also of fluids and the strengths of materials and his own description of the scientific method. He’d pestered scientists and astronomers from around Britain for data on the planets and the tides.

Figure 6.3: A portion of De Motu in Newton’s hand in 1684, written for John Locke who was an early reader of Principia.
He’d made measurements of motion in his own lab. He let his alchemy furnace go out forever as he worked solely on his “system of the world.” The arguments were mathematical and constituted the first workable model of motion, kinematics and dynamics, and also gravity (later). He continued to hide his calculus, preferring to speak in terms of limits and extrapolations using geometrical constructions, surely backed up by his own private calculus-based calculations. Principia went through three editions after the original 1686 start, often with him revising his last chapter, which was more philosophical, but also with successive furious deletions of the names of rivals.
Halley had persuaded the Royal Society to act as the publisher of Principia and Newton dedicated it so. But the coffers of the Society were dry when it came time to print as they had used up their entire accounts in a lavishly illustrated two volume, History of Fishes.
So Halley took a deep breath and paid for the initial publication himself. This of course led to his active interest in encouraging Newton to push the book off at booksellers and libraries himself. Never was there a more generous gift to science than Halley’s unselfish gesture. And for a book that only a few people in the world could read, but a book that quite possibly initiated the Enlightenment and people’s relationship to our universe.
–>
6.4 Impulse: Getting Going
Newton’s mechanics and many of the concepts we’ll concern ourselves with, from electromagnetics to quantum mechanics to astrophysics, rely on the idea of a force. It’s a common word, one of many that bear responsibility for everyday speech as well as specific, technical speech. Your common experiences with forces are all around you and you’ve instinctively learned to use everyday forces to move around and compensate for forces that threaten you. But your experiences with technical forces are probably related to weighing yourself or other things (that is, measuring the force that the earth pulls on something) and putting air in your tires (measuring the pressure that your tire presses against the tire’s walls). There you deal with the US units of force, namely the pound (lbs), or in the case of your tires, pound per square inch (psi). We’ll need to dig deeper than this, but whenever you see “pounds,” you’re talking about forces.
In a conventional physics course, Newton’s Three laws of mechanics would be a major focus of study. In QS&BB we don’t need that depth, but we do need three important concepts…the ones that underpinned his system: the concepts of force, mass, and momentum. Let’s move:
In the previous lesson we laid out the rules that govern an object’s motion, including whether it moves at a constant speed or accelerates. What we conveniently avoided was what causes motion — on that score Galileo had nothing to say. (Remember that Descartes insisted on the cause of things before beginning to work on the outcomes? He explicitly denigrated Galileo’s work because Galileo explicitly avoided speculating on why an object would accelerate — its cause.)
Of course Aristotle had something to say about everything and as we saw in the last lesson he insisted that unnatural motion is not for free, that one always needs to apply a contact force to start something to move and then to keep it going. Natural motion is for-free for him. No explanation of how, just that weird desire that heavy, falling objects have for the earth. There’s so much that’s wrong with both of these ideas that it’s difficult to know where to start!
One of the many ways that Isaac Newton got into the textbooks was to argue with Aristotle: No. Constant motion is free. It’s only accelerated motion that requires payment in the form of the action of a force. Further, while Aristotle simply declared what his rules were, Newton built the first-ever mathematical model describing them. Remarkably, his model has functioned for four centuries and still forms the basis of mechanical and civil engineering — even NASA projects.
To start something moving from rest? Apply a force. To speed up or slow down something already moving? Apply a force! To cause something to deviate from a straight line? Yes. Another force. To keep something moving at a constant speed? No (net) force required, thank you.
Here’s what he said:
Whenever there’s a change of velocity, a force is at work: forces are responsible for acceleration.
These are Newton’s conclusion, but let’s start slowly and sneak up on this idea. Impulsively.
6.4.1 Impulse In Practice
Newton: To get something up to speed, you need to whack it or shove it — either a sharp collision or a steady push increases the speed of an object. Push harder? More speed. Push longer? Again, more speed. And as you know from any sport involving a collision, something that’s moving fast can in turn exert a bigger force than something that’s moving slowly.
So let’s codify that everyday notion into a model of forces and motion. Let’s imagine a force, F that pushes during some time interval, \(\Delta t\). A whack means that \(\Delta t\) is small (like a golf club hitting a ball) while a steady shove (like a rugby scrum) means that the force is slowly applied so \(\Delta t\) is larger.
Here’s what we know from experience: applying a force (\(F\)) to something for a time interval (\(\Delta t\)) results in the speed increasing in proportion, (\(\Delta v\)). We have the beginnings of a model:
\[\begin{equation} F\Delta t \propto \Delta v. \tag{6.1} \end{equation}\]
Increase \(F\), \(\Delta t\), or both on the left-hand side, and the speed goes up on the right-hand side. The quantity on the left side is called the Impulse. It’s the sports-quantity. Any game involving a ball involves impulse and exceptional athletes can control both the \(F\) and the \(\Delta t\). The quantity on the right implies that the speed changed and of course if the speed changed, then the object accelerated.
We need to refine the model. But first some units and language:
May the force be with you by so many different names
We will use forces many times in QS&BB, which is a common quantity in our lives because of “weight.” But if you’re from the United States, when you step on the bathroom scale it reports back to you your weight in the Imperial measurement system (or “customary measures system”) as too many Pounds, lbs. In a minute, you’ll see why that’s confusing when comparing to the rest of the world where the bathroom scale would report kilograms.
In any case, the unit of force in the International System of Units (SI), which includes the older “metric system” or MKS (Meter, Kilogram, Second) is the Newton, N. If you go to the gas station in Berlin, you’ll fill your tires to a pressure measured in Pascals, which is Newtons per square meter. Of course up the street from me, our Michigan gas station reports pounds per square inch for my pressure.
We’ll predominantly use the unit of Newton as the modern measure of a force — like the rest of the civilized world. `As I’ve said, we’ll not obsess with units and so I’m happy for you to rely on Mr. Google in almost all instances. Let’s practice:
🖋 📓
Please study Example 1: convert Newtons to Pounds
🖥️
Please answer Question 1 for points: Pounds into Newtons and flour
6.4.2 Inertia
Pressing forward (see what I did there?). Let’s think about pushing.
Suppose I apply a force of \(F=100\) pounds for 60 seconds to a Volkswagen and you apply a force of \(F=100\) pounds for 60 seconds to a little red wagon. We both begin our efforts at point A:
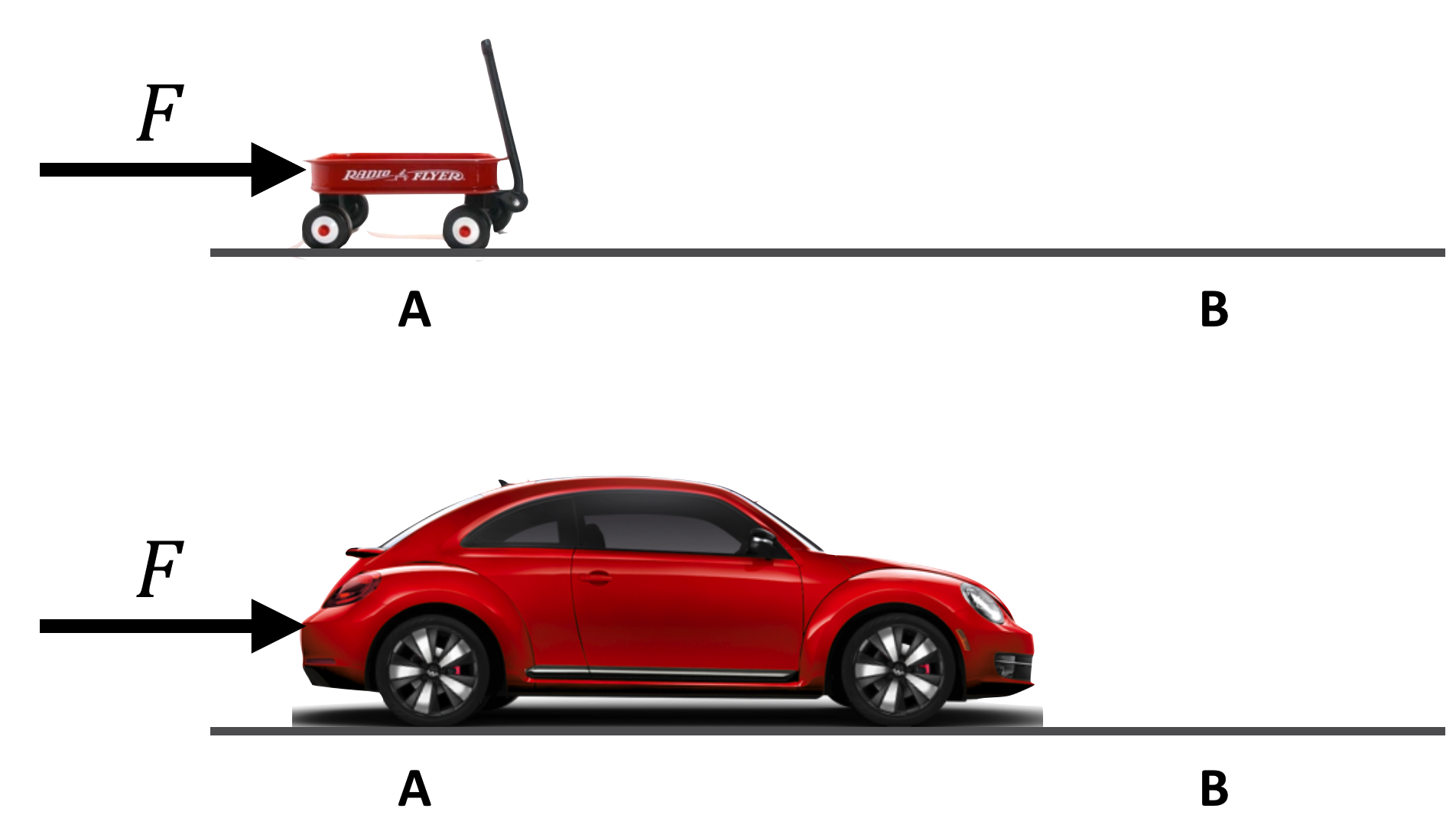
Figure 6.4: The same force applied to two red objects, of very different sizes.
Will the resulting \(\Delta v\) at point B be the same for both vehicles?
Of course not. The little red wagon will gain more speed than the Volkswagen (regardless of its color). The VW is more reluctant to be accelerated than the wagon. So Eq.(6.1) is not the whole story. What’s missing is just that reluctance that any object has to being accelerated, which has a name: inertia.
🎥
Have a look at this 6 min video example 1: the beetle and the wagon
Inertia is the resistance that an object has to being accelerated.
Wait. What if the VW had been blue rather than red
Did you really ask that? Stop it.
6.5 Newton’s Mass
Mass is a toughy and we’ll see over and over how complicated it is — to the current day. Here’s how he defined it in the Principia:
“Mass is the quantity of matter arising from its density and bulk conjointly.”
There you go. Useful? …no?
Wait. Doesn’t that seem circular?
Glad you asked. You might think so, yes. You know that density is an object’s mass divided by its volume and so to define mass…using mass…does seem so. I think it’s probably hard to invent your own science out of almost nothing! So word-explanations can seem a little strange. (There’s also some reason to think that “density” for Newton referred to specific gravity, but let’s not follow that.) You’re correct to be a little unsatisfied with this definition! But we can forgive him since “mass” becomes almost a theme in QS&BB. It’s really complicated!
In any case, you do perfectly well—at least in solving engineering homework or building bridges—to accept the idea that mass is the amount of the “stuff” in an object and that it’s also the quantitative measure of an object’s reluctance to be coaxed into changing its motion.
Here begins our love-hate relationship with mass. This much works:
Inertia is an object’s resistance to being accelerated and the measure of an object’s inertia is its mass.
This is the most profound and at the same time, the most mundane idea that Newton had! It’s with us today as a primary focus of particle physics research:
What is the nature of Mass?
At the deep level of elementary particles, mass confuses us, perhaps in a different way from how it confuses engineering freshmen. We think that mass may actually not be an actual property of object, but rather a result of an object’s interaction with a spooky field that sprang into existence just after the birth of the Universe. Now, in the 21st century, we’ve got a whole new set of neuroses about this subject, as understanding it occupies almost the entire Particle Physics community. So, Mass has been a problematic subject since its beginning in Newton’s hands.
And then, there are units. The MKS unit for mass is the kilogram, kg and we’ll use it almost universally. So remembering the bathroom scale discussion above, you can now see that US bathroom scales report a force while for everyone else in the world, their scales report people’s masses, kg. But their scales, like ours, are still measuring the earth’s force on us but their readings are calibrated to report back mass, not force. Their scales will not work to Mars without difficulty. We’ll come back to this.
With this “feeling” for pushing on big and little things, we can state the impulse proportionality as a full-fledged model — an equation.
6.6 The “Quantity of Motion”: Momentum
We just developed a sense that our hand-built, car-pushing formula, Eq. (6.1)has to depend on speed and mass and so we’ll just add it in on the right-hand side to get:
🖋 📓
\[\begin{equation} F\Delta t = m\Delta v \tag{6.2} \end{equation}\]
Being more explicit, when fleshed out impulse is
\[\begin{equation} F\Delta t = m(v - v_0) \tag{6.3} \end{equation}\]
There’s more to this story
To be totally correct, the right hand side of this equation can be written as \(\Delta (mv)\) which recognizes that the mass might change instead of, or in addition to, the velocity changing. This is how a balloon jumps from your hand when you stop pinching the nozzle, or how a rocket is propelled by ejecting burned propellent out the back. In each case, the mass of the moving object changes and that results in a thrust. But we’ll not encounter that in QS&BB.
This quantity on the right, \(mv\) is momentum.
6.6.1 Momentum In Practice
This was Newton’s second good idea: the concept of “momentum” which he called the “quantity of motion” — a nice description, I think. The idea that a moving object possessed something — some quality — was pretty hard to ignore. But, nobody could figure out how to describe it for 2000 years before him. Aristotle just denied it: “No,” a moving object doesn’t possess any quality. Galileo vaguely said “yes,” there is something “in” a moving body that he called impetio. Kepler seemed to say “yes.” Descartes definitely said “yes.” Newton agreed with his 17th century predecessors but made the idea useful.
🖋 📓
What he concluded was that the “quantity of motion” is momentum. Keeping with tradition by using the symbol “p” as its nickname, momentum is:
\[\begin{equation} p = mv \tag{6.4} \end{equation}\]
With this now we can continue the manipulation of Eq. and restate it one more time in terms of momentum:
\[\begin{equation} F\Delta t = \Delta p \tag{6.5} \end{equation}\]
Remember, sports with balls are delivery vehicles for impulse questions:
🖋 📓
Please study Example 2: Big Boat
🖥️
Please answer Question 2 for points: golf and impulse
How about stopping? Violent stopping? Besides, you’ve wondered when an apple question might appear.
🖋 📓
Please study Example 3: applesauce
🖋 📓
Please study Example 4: SpaceX docking at ISS
🖥️
Please answer Question 3 for points: more applesauce
We’re going to find that momentum is the most important quantity in our particle physics story.
We’ll use it over and over in different guises.
The sports quantity
Equation (6.5) works in three ways: either you know the force and you use the formula to calculate the change in momentum in a given time. Or, you know the change in momentum and you use it to calculate the total force in a given time, or you adjust the time for a given force.
Now you’ve gotten the formula that governs all sports involving whacking one thing with another, like baseball, golf, tennis, soccer, or football. Think about what you almost always want to do: you want to make the ball go faster after you hit it. That means, you want the change in the momentum to be the highest possible. So, Eq. (6.5) tells you how: you hit the ball as hard as you can (that’s a large \(F\)) and you get “good contact” (which means you hit the part of the bat or racquet or club where you can touch the ball as long as possible…which is the largest \(\Delta t\)).
This also explains how airbags and bumper-crumple zones in automobiles work. There, you know what the change in momentum is: \[F\Delta t = m\times (v_{after}-v_{before}).\nonumber \] That’s the change where the final velocity is zero (the car stops). The initial velocity is fixed and so \[v_{before}\] has to be divided up between the force and the time in \(F\Delta t\) where the force is applied, say to your bumper. High force is not good for the occupants inside the car, so this leads to the design goal of spreading out the time—large \(\Delta t\) so that the force will be smaller. This is the same reason that you bend your legs when you jump off a table and hit the floor!
6.6.2 Momentum Is a Vector
Because velocity is a vector, momentum is also. In the next lesson when we consider collisions, which is where momentum shines in QS&BB, the direction-part of the momentum vector will play a crucial role. For that matter, since momentum and force are vectors the actual general statement about Impulse is:
\[\begin{equation} \vec{F}\Delta t = \Delta \vec{p} \tag{6.6} \end{equation}\]
Here’s a buzz-word: “state.” If you give me the position and the momentum of any object—I know everything I need to know to predict where it will be at any subsequent time. In Newton’s world, which is good enough for us for a while:
An object’s position and its momentum are called its “state.”
6.7 Newton’s Famous Three laws
Newton’s momentum and mass are at the heart of his three laws of motion. Let’s go through them in words, and then one of them in more detail algebraically.
Newton’s 1st law of motion says that anything that’s moving at a constant speed (which could be zero) will continue in that way unless a force acts on it. That’s a statement about inertia—resistance to acceleration. (Newton inherited this idea from Galileo, Descartes, Isaac Beeckman, and Marin Mersenne, but gave it a quantitative meaning.)
Newton’s 2nd law of motion says that momentum is changed when a force acts on an object for a duration of time. Or, you might have learned it as a defining statement about “force” namely:
Force is equal to the rate of change of momentum.
Newton’s 3rd law of motion is subtle, and solely due to Newton’s ingenuity. It says that if you push on something—anything and with any amount of force—that object—will push back with exactly the same force. We’ll think harder about the 3rd law when we talk about collisions.
6.8 Newton’s Second law
Students in a physics class become intimately familiar with the 2nd law, which is all about momentum and how to change it. A simple arrangement of the (6.6) relation yields the real mathematical definition of Newton’s 2nd law:
\[\begin{equation} \vec{F}=\frac{\Delta \vec{p}}{\Delta t}. \tag{6.7} \end{equation}\]
\[ \vec{F}=\frac{\Delta \vec{p}}{\Delta t}. \label{second1} \]
Maybe you’ve maybe seen this equation but written in a different way. Inserting back the definition of momentum, \(p=mv\) (in one dimension, so we’ll drop the vector notation):
🖋 📓
\[\begin{equation} F=\frac{\Delta p}{\Delta t} = \frac{\Delta mv}{\Delta t}. \tag{6.8} \end{equation}\]
\[ F=\frac{\Delta p}{\Delta t} = \frac{\Delta mv}{\Delta t}.\label{second2} \]
Let’s assume that the mass of the object doesn’t change, so we can push the \(\Delta\) operation through the mass and let it act directly on the velocity and get
\[\begin{equation} F=\frac{m\Delta v}{\Delta t} \tag{6.9} \end{equation}\]
\[ F=\frac{m\Delta v}{\Delta t} \label{second3} \]
and what’s \(\Delta v / \Delta t\)? That’s nothing more than acceleration, so we finally arrive at the T-shirt version of the famous Newton’s Second law of motion:
\[\begin{equation} F=ma. \tag{6.10} \end{equation}\]
\[F=ma.\label{second4}\]
Notice that if you isolate the acceleration by dividing both sides by \(m\),
\[ a = \frac{F}{m} \nonumber \]
you get the force divided by the mass. There’s the “inertia” nature of mass making its appearance: the larger the mass (so that \(\frac{1}{m}\) is a small number) the harder it is to accelerate for a given force (the Volkswagen)—\(a\) is small. On the other hand, if that force is now applied to a light object (so that \(\frac{1}{m}\) is a larger number) then the acceleration will be greater (that’s the wagon).
🖋 📓
Stare at Eq. (6.7) : if you think about it, there are three ways for \(\vec{p}\) to change:
As we’ve just seen, if the speed changes, the velocity vector changes, so then the momentum vector changes. That’s easy and what you’d expect.
If the mass changes, then the momentum changes.
- If the velocity vector changes, but the speed stays the same? Ah. That’s interesting, and we’ll look at that carefully in section Circular Motion below.
#1 makes sense in our everyday lives. If you change the speed, the velocity will change. #2 is less obvious but think about pinching the opening of a balloon that you’ve blown up. The balloon’s mass consists of the stretchy material of the balloon plus the mass of the air inside. Held out in front of you there is no net force and it’s at rest in your hand. Puncture it with a pin and the air rushes out fast and so the mass of the air inside the balloon rapidly decreases. The consequence of that decrease in mass, a \(\Delta m\) in a time \(\Delta t\) all by itself results in a change in the momentum of the balloon! That’s how rockets work. For #3 we’ll wait a bit.
Let’s play with this on a trip:
🖋 📓
Please study Example 5: AIRBUS accelerating
6.9 Weight
I’ve been toying with you over units so let’s clean this up. Since we’re Earth-bound we tend to mix up the units of weight and mass at the grocery store. You’ll appreciate that in a bit.
A gram is a unit of mass, (1000 grams in a kilogram) while an ounce is a unit of force (16 ounces in a pound). A kilogram still a measure of mass and a pound is a measure of weight. But we get away with using both systems since we tend to buy things and compare them on Earth. If we had a Mars colony, well then there would be trouble. If you put that 5 Earth-pound bag of Gold Bond flour from Kroger on your bathroom scale which you transported to Mars, it would read back about 2 pounds. But in each location, the bag of flour would still have a mass of 2.27 kg. How can that be?
Weight is a special kind of force—still subject to being the “\(F\)” in Newton’s 2nd law, but called out as a unique characteristic of massive objects on the Earth.
What Galileo showed was that the acceleration due to gravity near the surface of the Earth is a particular value—he presumed it was a constant. If the ground disappeared beneath your feet, then because you have a mass, you’d start to fall towards the Earth’s center with that acceleration of g. But happily the ground pushes back and you are stable on the surface. (It’s a little confusing since you’re not moving but you’re still accelerated) So from Newton’s Second law, when we have a mass and we have an acceleration, we can calculate a force and we define that particular force of attraction by the Earth as the the object’s weight.
🖋 📓
Let’s call it w and we can write it out:
\[\begin{equation} w=mg. \tag{6.11} \end{equation}\]
Notice that this is just Newton’s 2nd law, but with a particular acceleration, \(g\) which leads to a particular force, \(w\).
Weight is the force that a planet exerts on an object on its surface.
We can measure an object’s weight by making use of the fact that the Earth pushes back with a force that’s the same value as the weight. When you “weigh” something, probably a spring is doing the pushing-back. There’s one in your bathroom scale which is calibrated in the U.S. to read that push-back in pounds. In France, that reading would be in kilograms (but it’s still a spring, so really measuring weight and converting to mass)! Basically everyone (else) in the world deals in mass terminology. We’ll see how the Earth does this in a bit when we get to Newton’s other law, that of Gravitation.
By the way, the acceleration due to Mars gravity, its “little \(g_M,\)” is about 4 m/s\(^2\), to compare with our “little \(g_M,\) of about 10 m/s\(^2\). That explains why that bag of flour appears to be light using your Earth-calibrated scale.
I have bad news: unfortunately in the English system, the unit of mass is “slugs.” Now I have good news. We’ll not use slugs for anything in QS&BB.
Wait. Seriously. Slugs.
Wish you’d not asked. I confess I don’t know the origin of the “slug.” One of life’s mysteries.
So we can collect our units appropriate to Newton’s Second law in this table below. In the last column, the standard abbreviations are shown as well.
6.9.0.1 Mass, acceleration, and force conversions
| English - MKS | |||
|---|---|---|---|
| acceleration | ft/s\(^2\) | m/s\(^2\) | 1 ft/s\(^2\) = 0.305 m/s\(^2\) |
| \(g =\) 32 ft/s\(^2\) | \(g = 9.8\) m/s\(^2\) | ||
| mass | slugs | kilograms | 1 slug = 14.59 kg |
| on earth | mass of 1 slug | mass of 1 kg | |
| = weight of 32.2 lbs | = weight of 9.8 N | ||
| force | pounds (lb) | Newtons (N) | 1 lb = 4.45 N |
Weighty conversions.
🖋 📓
Please study Example 6: my weight
🖥️
Please answer Question 4 for points: VW weight
Let’s go for a ride:
🖋 📓
Please study Example 6: to become a capa problem
🖥️
Please answer Question 5 for points: the BIKING EXAMPLE!!
6.10 Finally, Nothing: Forces in Balance
We’ve been dealing with Newton’s 2nd law as if there’s only one object and one force, but what it really says is more general (but where the mass remains constant):
\[\begin{align*} \text{add up all forces on an object } &= ma \\ F_1+F_2+F_3 + \ldots & =ma \end{align*}\]
Here are three example situations:
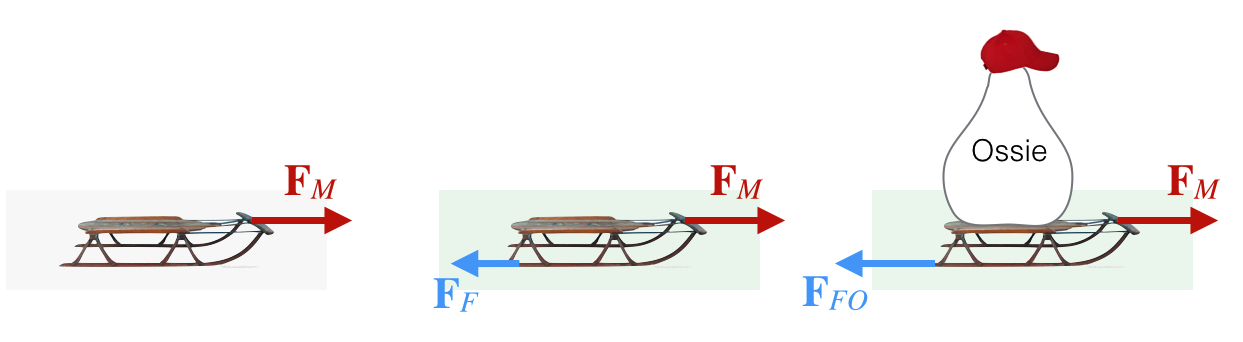
Figure 6.5: The left figure imagines a single force with no friction, like pulling a sled on smooth ice. The middle figure assumes that Mo is pulling the sled across grass, so there’s friction. The right figure imagines that Ossie is sitting on the sled which makes the friction more and adds to the overall mass. Notice the relative lengths of the two friction forces, with and without the added Ossie-load.
The simplest example: Mo is pulling his vintage wood & cast-iron Mickey Mouse Flexible Flyer sled across a frozen pond. He’s a strong guy and he can apply a pretty steady force, which we’ll call \(F_M\). In that case, while he pulls, he’s working out the acceleration in his head:
\[ F_M=m_Sa_S \nonumber \]
He pulls with \(F_M\), the sled has mass \(m_S\), and the sled accelerates at \(a_S\). Mo, while book-brainy is not too everyday-smart.
While he enjoys sledding in the winter, it’s too cold during that time so he prefers to do his sledding during the summer. In order to get to his favorite hill, he has to drag his sled across the grass. Carefully calibrating his force again, he pulls at the same value of \(F_M\) but doesn’t achieve the same enthusiastic acceleration as on the ice because of the friction which is responsible for a force that points in the opposite direction, \(F_{F}\). Now his acceleration is
\[ F_M-F_F=m_Sa_S \nonumber \]
So clearly the sled’s acceleration is less than in the cold months. The value of the frictional force, \(F_F\), depends on how hard the sled is pressed against the grass and scales just about evenly with the mass of the sled.
Mo’s friend Ossie prefers to not walk and so he rides on the sled and so the mass that Mo needs to work against is that of the sled plus Ossie, \(m_S+m_O\). Ossie presses the sled into the grass more so its frictional force, \(F_{FO}\), is also more and it just balances Mo’s steady, determined force, \(F_M\), so \(F_M=F_{FO}\), or:
\[\begin{align*} F_M-F_{FO} &=(m_S+m_O)a_S \\ F_M-F_{FO} &=0 \end{align*}\]
So when the forces balance, there’s no acceleration. When there’s no acceleration, the speed doesn’t change. So can Mo still get to his warm hill? Why yes, if he got the sled up to some speed (say Ossie doesn’t get on until it’s moving) then it will continue at that speed, which is another way to say that it does not accelerate. Which is another way to say Newton’s 1st law is at work.
You already have an intuitive feel for this force-balancing act. Because, tug of war:
🖋 📓
Please study Example 7: tug of war
🖥️
Please answer Question 6 for points: more tug of war
6.11 Circular Motion
In Eq. (6.7) the relationship of force to the vector momentum is subtle, but you use it and experience it every day. Suppose Hazel and Ira are a passengers in a car going around a curve. When they enter the curve, they’re moving north. When they emerge from the curve, they’re pointing west. Hazel is driving and watching the speedometer carefully in order to make sure that they remain at the same speed through the whole path. So did their speed change? No! Did their velocity change? Yes! Because, the direction of their speed changed. This is shown in the figure:
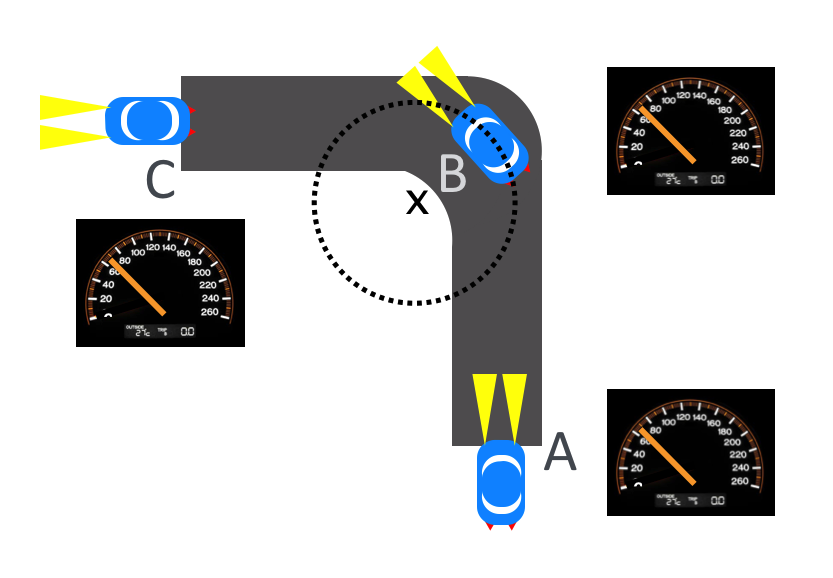
Figure 6.6: A car going around a curve at constant speed: at A, its speedometer reads 60 mph, at C, 60 mph, and as it’s going through the curve, also 60 mph. During the period when it’s going around the curve (when the steering wheel is turned), for a brief time it traces out a segment of the dashed circle with its center shown at x.
Let’s think in terms of momentum and this diagram shows the momentum vectors at A, B, and C:
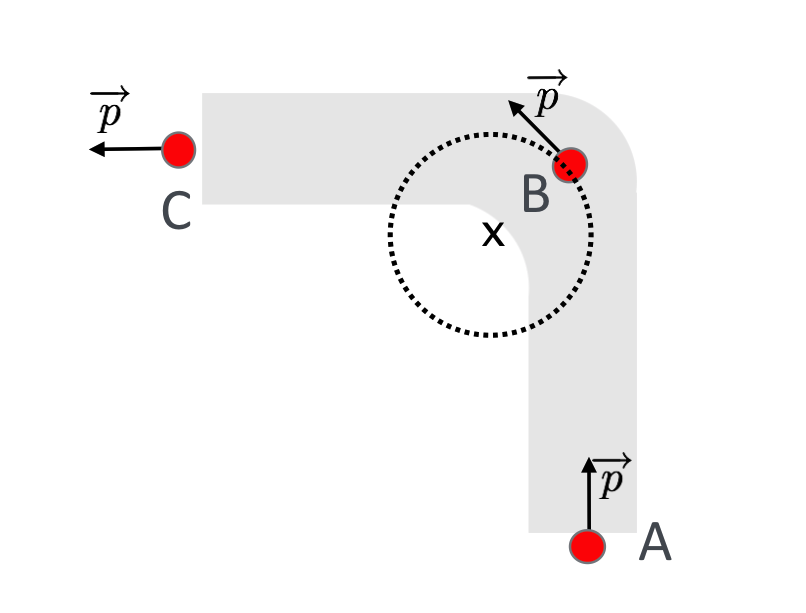
Figure 6.7: caption
Let’s recite the series of events that follow from going around this curve: Hazel and Ira both remain in the car, so somehow they are both “forced” to deviate from straight-line motion along with their vehicle. A variety of phenomena cause that to happen: Hazel’s smart and is wearing her seatbelt. That keeps her attached to the car as it turns. Nobody can tell Ira what to do, so he never wears a seatbelt and slides across the seat and is pressed up against his door and that keeps him moving in a circle. Each of these phenomena constitute forces that act in a direction pointing to the inside of the circle that their car is moving—the point labeled x in the figure. Let’s state some obvious, but subtle things about this simple act:
Their speed didn’t change.
But, their direction changed, so their velocity changed.
If their velocity changed then their momentum changed (from the definition of momentum, \(\vec{p}=m\vec{v}\).
If their momentum changed, there had to be an inward force applied to both of them. (from the 2nd law).
These various forces all caused them to go in the same circle as the car (Second law) while they are trying desperately to continue to go straight (First law!). (In fact, Ira had an apple in his hand and when the car turned left, he let go and the apple kept going straight north, out of the open window.)
The forces are:
- The seatbelt pulled on Hazel;
- Ira experienced a frictional force between his jeans and the seat but it but was not enough to keep him from sliding;
- so he slid until he pressed against the door and then the door applied a force;
- and the tires of the car also have a frictional force to the pavement and that points “in” as well…in fact, that’s the only way that a car ever turns a corner.
Each of these forces points “in” toward x, the center of the circle and they all do the same job: pull the objects towards that center. These kind of forcing-in-a-circle forces have a special name:
A force that causes motion to deviate from a straight line is called “centripetal force.”
Another pretty good idea of Newton’s (and Christiaan Huygens’).
6.11.1 Newton’s Reasoning
The essence of circular motion can be visualized in this cartoon:
where a figure is twirling a ball attached to a rope in a circle. Let’s ignore gravity for a second and concentrate on the motion in the plane of the rope and ball…and his fist. You know by now what would happen if he let go of the rope. Without the rope pulling in towards the center, there is no horizontal force and according to Newton’s First law, the ball would go straight. (That’s a sling-shot.) So the rope is causing the ball to deviate from a straight line. Can you agree that the rope is doing the same thing that the seatbelt and tire friction do?
🔎
Have a look at a deeper explanation for how the pull is to the center of the circle
Whenever an object deviates from a straight line path, there must be a force pointing perpendicular to that path. For the simplest such motion — moving in a circle — that force points to the center of the circle. Newton (and Huygens, see the next lesson) envisioned circular motion this way:
- the object tries to go straight
- it’s tugged to the center (the rope)
- it tries to go straight again!
- and again, it’s tugged toward the center
Over and over this motion can be thought of as jagged straight-jerk, straight-jerk…but if the tugs are infinitesimally close together in time, then the result is a smooth circle, and not a jagged path.
If there’s a perpendicular force to the center, then there’s also an acceleration toward the center. These are both special things and have their own formulas to represent them. They also have a special name: “centripetal.”
Why is there an acceleration? Even if the objects speed is constant? It’s because while the speed is not changing, the direction is. Here the vector nature of the velocity (or momentum) is a big deal and it matters!
6.11.2 Centripetal Force and Centripetal Acceleration
If this understanding of circular motion weren’t enough, Newton went a step further in his paranoid sort of way. He actually found a relationship for what the centripetal force would be and did it both using his new calculus and in a strictly geometrical fashion. The latter he published in Principia, and like other such derivations, kept the calculus version to himself. Why? He feared being scooped. Calculus was his (“my precious”) private tool for a long time.
I’ll just enunciate the result without his tedious geometrical explanation or the more complicated calculus explanation.
The essence of this is shown on the left and right figures here, where we see a representation of the momentum vector and the centripetal force, \(\vec{F}_C,\) on the left, and following Hazel and Ira’s experiences, pointing to the center.
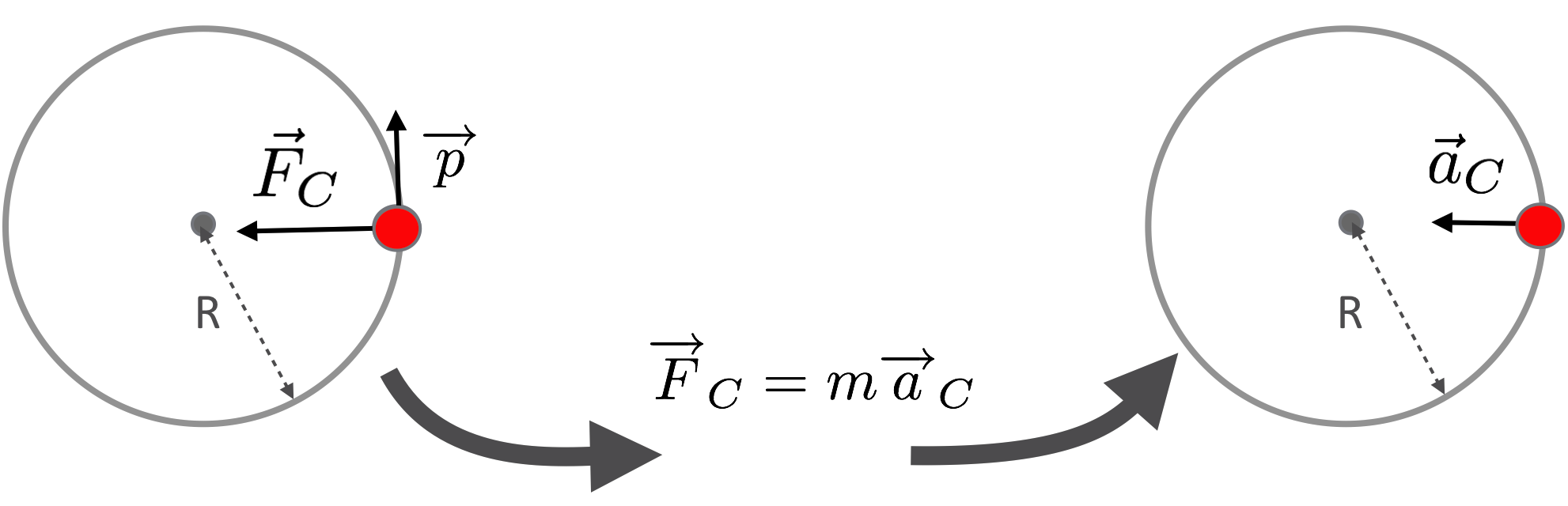
Figure 6.8: Centripetal force points to the center and centripetal acceleration does the same thing.
But where there’s smoke, there’s fire…or rather, where there’s a force, there’s an acceleration, because \(F=ma,\) right? The right hand side of the figure shows this “centripetal acceleration,” a different vector but pointing in the same direction as the centripetal force vector. So we have:
🖋 📓
\[\vec{F}_C = m\vec{a}_C.\]
Here’s the punchline for centripetal acceleration:
Centripetal acceleration is special and has a very particular form (found by Newton and his Dutch competitor, Christiaan Huygens) for all curvy motions. It’s
\[a_C=\frac{v^2}{R}\]
Here, \(R\) is the radius of that circle and \(v\) is the magnitude of the velocity. So, we have for circular motion only:
\[F_C=m\frac{v^2}{R}.\]
The speed of an object moving in a circle is of interest and it’s easy to model that by multiplying the \(F_C\) by \(R\) and dividing by \(m\):
\[v^2 = \frac{F_C R}{m}\label{vcentrip}\]
There are two ways to use this concept:
- If you want something to move in a curved path at a particular speed, you can calculate and apply a precise (centripetal) force—tug it—to make that happen. Depending on the curve (\(R\)) and the speed you want, you can dial up the \(F.\) This is instinctive…your muscle-brain connection does it all the time.
- If you see that an object is not moving in a straight line, then there has to be a centripetal force being applied somewhere! You should be able to find the cause, or infer a cause.
Sometimes identification of such a force is tricky. Remember that in Hazel’s car, what actually causes the car itself to go around a circular curve is the force of friction between the road surface and the four tires of the car—four little force vectors all pointing along the road-tire interface towards the center. Each little \(F_C\) adds together to equal the \(F_C=m\frac{v^2}{R}\) involving the speed and the turning radius. Here \(m\) is the mass of the car plus that of its occupants (less that apple that went out the window).
- Reduce the stickiness of the road (ice, snow, rain?) and that friction force is reduced on the left — we’ve all been there — and that available force is reduced, sometimes considerably. You instinctively know this, so you drive slower (reducing \(v\) in the numerator to match the \(F_C\) that can be produced by the tires and road given the conditions.
- Make the turn tighter and so the \(m\frac{v^2}{R}\) goes up and it better be balanced by the tires’ stickiness on the road.
If any of these limits are reached, you cease doing circular motion and Newton’s 1st law wins and you start going straight. Not good in most circumstances where the road curved.
🖋 📓
Please study Example 8: Everyone’s favorite playground device not requiring an apple
🖥️
Please answer Question 7 for points: Olympics…sort of
🖋 📓
Please study Example 9: NCAA hammer throw
🖥️
Please answer Question 8 for points: Centripetal force for hammer throw
6.12 What to Remember from Lesson 6?
This has been a big lesson with lots of ideas. Here’s what we’ll refer to in lessons to come.
6.12.1 Force and Acceleration
The T-shirt equation, Newton’s 2nd little-l law is simple and we’ll not require any sophisticated or tricky use of it:
\[F=ma \nonumber \]
If there’s a force on an object, then that object will accelerate. The larger is the mass of an object, the more force is required to accelerate it, or the smaller will its acceleration be. All common-sense ideas nicely packaged in this simple model for acceleration.
6.12.2 Mass and Momentum
Mass is the resistance to being accelerated—its nickname is inertia. You knew that, but now Newton’s 2nd law embodies it:
\[a =\frac{F}{m} \nonumber \]
big \(m\), small \(a\).
Momentum is the oomph that an object moving at a speed has. It’s a little bit of mass and a little bit of velocity and together they make momentum:
\[p=mv. \nonumber \]
6.12.3 Weight
Still going with \(F=ma\), but now for a particular acceleration, that of gravity near the surface of the Earth. That force is nearly constant and so the acceleration is nearly constant and we give it a special name, \(g\)…”little gee.” It’s actual value is \(g=9.8\) m/s\(^2\) but we can often get away with using \(g=10\) m/s\(^2\) and I’ll do that whenever I can.
6.12.4 Circular Motion
The model for circular motion will recur a number of times. Just remember that
\[F_C = ma_C = m \frac{v^2}{R} \nonumber\]
or its alter-ego,
\[v^2 = \frac{F_C R}{m}\]
which has the merry-go-round experiences encapsulated in this one-line formula. If the force is constant, for any object “making a turn” (or in an orbit!), the further it is from the center of its circular path, the faster it will go. For everyday life, where the centripetal force responsible for keeping an object moving in a circle (tires, seat belts, jeans-on-the merry-go-round, the rope overhead). These frictional or tension forces have a limit and when that’s reached, straight line motion is the result! We’ll encounter circular motion with a force that’s not constant, you just wait.
But first, let’s bang things together.






