11.4. Forces from Electricity: Coulomb’s Law#
Amounts of charge were very difficult to determine and of course their actual nature was unknown. Charles Coulomb was a French mathematician-military engineer who was exceedingly proficient with instruments and in 1784 succeeded in building a very delicate “torsional balance” of precisely machined metal balls. These he would attach across a lightweight beam, which in turn was suspended at its center by a thin wire. Gently pushing the balls in a plane around the center of the brace would twist the vertical wire and that twist could be precisely measured and converted into the force of the push. By charging the suspended balls and separatley, the fixed, external balls to create a push (or pull), Coulomb was able to determine the amount of force exerted by given amounts of charge, and the degree to which this force changed when the charges were separated.
Pencils Out!
Rather surprisingly, he found this force has a familiar form:
\(Q\) or \(q\) The letter \(Q\) is used for electrical charge. I’ll sometimes use \(Q\) or \(q\) to refer to the charge of a sub-atomic particle, when it matters.
which today we call Coulomb’s Law, the force between two charge collections \(Q_1\) and \(Q_2\), which are separated by a distance, \(R\) as shown in the figure. The value of the constant in front, \(k_E\), depends on the units employed. Using “Coulombs” as the unit for charge, along with meters for the distance, \(k_E\) can be determined in MKS units to be:
which is called Coulomb’s Constant.
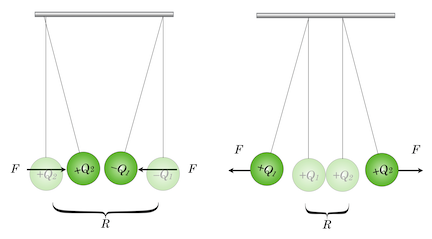
On the left, two charged insulating balls with opposite charges attract and on the right, with same-sign charges, repel.
Notice that Eq. 1 suggests that the electrical force depends directly on the magnitudes of the charges and the inverse square of the distance that charges are separated. The constant of proportionality, \(k_E\), is arbitrary until the units of charge and distance are specified. Notice that the sign of the charges matters here. Maintaining Franklin’s designation of plus and minus, if we make one of the charges plus and the other minus, then the force in the equation is algebraically negative. So, this means we have to be very careful about what force is on “whom.” Here’s how to think of it: If we draw an arrow from charge \(Q_1\) to \(Q_2\), then Equation @ref(eq:coulomb) represents the force on \(Q_1\) due to \(Q_2\) and if the charges are opposite in sign, then they are attracted to one another and the negative sign in the force equation is just telling you that the force is in the opposite direction of the arrow you just drew. The unit for charge that’s commonly used is the Coulomb.
A Coulomb of charge is an ENORMOUS amount of charge. For example, a lightening bolt will consist of only 10’s of Coulombs.
Wait. Then WHY use it? Glad you asked. The definition of a Coulomb is historical (hysterical?) and has almost no bearing on real-life. But we’re stuck with it. A couple of examples will make this clear.
Please study Example 1:
Are you kidding me? This force is 2 billion (with a B) pounds. If this were the weight of some object, it would have a mass of \(W/g = 9 \times 10^9/9.8 = 918\) billion kg. That’s the weight of 10 Nimitz-class super-aircraft carriers—the attraction of the Earth to 10 aircraft carriers stacked one on top of the other.
Just let that sink in…with the emphasis on “sink.” Let’s make it worse. How many Coulombs is the charge of an elementary particle?
Please answer Question 4 for points:
Please answer Question 5 for points:
Please answer Question 6 for points:
Please answer Question 7 for points: