Eager to Do Damage: Potential Energy

8.5. Eager to Do Damage: Potential Energy#

If kinetic energy is the act of causing damage, Potential Energy is just what the name implies…”the potential” for causing damage! Hold a barbell above your foot and let it go, it will change the shape of your foot when it lands, and maybe the floor as well. That suspended weight possess the potential for doing Work, which it does upon landing and slowing down…through your foot and the floor. Notice that because it is held above your foot, going back to that last bullet above, its position is the determining thing: its height above the floor. Until it’s released, it’s held back from falling.

Below is the picture you should have in your mind:

Here is a mass, $M$ which is suspended above a table by a height $h$. Nothing happening until it's dropped. But it has potential...for doing damage to the wood, through the nail's penetration.

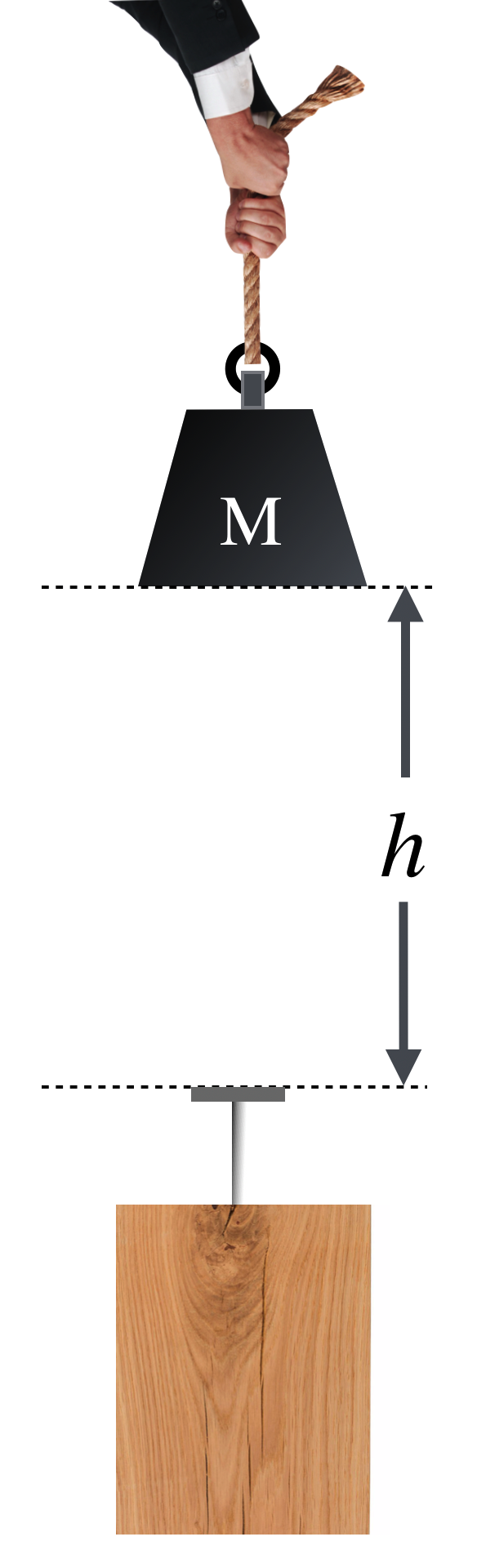
For dropping things in a uniform gravitational field, the Potential Energy (we’ll use the symbol $U$) is:

\[ U = mgh \nonumber \]

where $h$ is the vertical distance above the point defined to be the zero value of potential energy. Potential energy is a funny concept and I’ll have more to say about it when we talk about Einstein. It comes with a slippery feature that’s sometimes complicated to appreciate:

If I suspend the ball above the surface of a table, and if I assign the “zero” of potential energy to be that at the surface of the table, then when it falls to the tabletop, it has no potential energy left. But, if I take the zero of potential energy as that at the floor, then when it is done with its motion, still on the table, it still has potential energy left over relative to the floor — that associated with the height of the table. The difference between before (above) and after (the table) is still the same. Again, looking at the figure $h$ is the same distance whether it’s measured relative to the surface of the table or the floor. It’s the difference that counts.

**How much is potential energy? **

Let’s get a feel for the size of everyday potential energy. Remember that our 50 mph baseball had a kinetic energy of 35.1 J. Suppose I hold it over my head, which is about 8 feet, or 2.5 m above the ground. What’s its potential energy?

So the potential energy that the baseball has is

$$U=mgh = (0.145 \text{ kg})(10 \text{ m/s}^2)(2.5 \text{ m}) =3.6 \text{ J}$$

So Joules for potential energies are a pretty reasonable unit: few to hundreds of Joules in everyday life.

That’s sensible since $w=mg$ is the weight of the object, the force pulled on it by the Earth. So this too is a force times a distance, $U=wh$. The typical example of potential energy at work (no pun intended…or is there?) is driving a nail into a block of wood by dropping a weight from some height as shown below and above. Look at this carefully and understand the energy at each step, (a) through (e):

Let's bring Potential Energy home. In (a), can you drive the nail into the wood? No, there's no work done by $M$ just sitting there. In (b) we slowly raised it above the nail at a constant velocity to a height $q$ above the head of the nail and we hold it there. Then we let go so that as it falls, say at (c) it's gained speed and lost height. At (d) it has just reached the nail. It then drives the nail into the wood, stopping at (e).

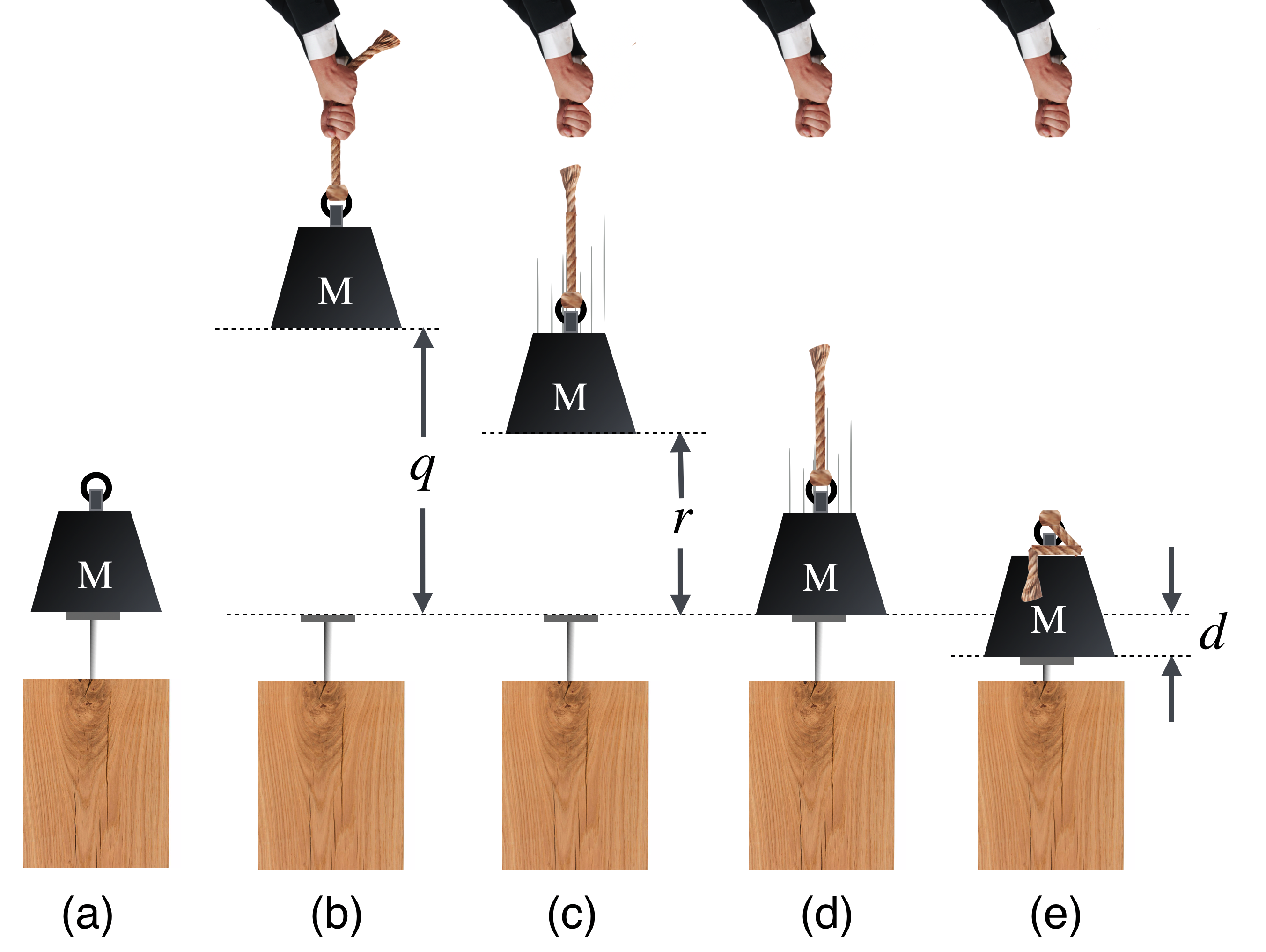
Here’s the energy progression:

We always have to define the point at which potential energy is zero: we’ll take the vertical position of the nail in (a) as $U=0$.
(a): $K=0$, because $M$ is not moving and $U=0$.
(b): Energy is put into the system by raising it: $U=Mgq$ because it’s now at a position where it could potentially do work but it’s constrained by the rope and $K=0$, because it’s not moving.
(c): $K$ is gaining, because it’s going faster and $U=Mgr$ is diminishing since $r<q$: it’s getting lower.
(d): $K$ is as much as it will be and $U=$ as it was in (a).
(e): Work has been done by $M$ on the wood and a force has been applied through a distance $d$ until it stops and all of the lost kinetic energy has warmed the wood and the nail. The work done is equal to the change in $K$ which is $K-K_0$ but since $K=0$ once the nail stops, the work done on the wood is numerically equal to the kinetic energy that $M$ had just before it touches the nail at (d).

Let’s work out the mathematical sentences that show the energy conservation in this process. In general, the potential energy at any height, $h$, is $U=Mgh$. We’ll describe the kinetic energy at any of the points as $K=\frac{1}{2}Mv(b)^2$, where $v(b)$ is the velocity at stage (b) in the diagram. Here we go:

\[\begin{split}\begin{align} K(b)+U(b) &= 0 + U(b) = K(c) + U(c) = K(d) + 0 = \bar{F}d \\ &= 0 + Mgq = \frac{1}{2}Mv(c)^2 + Mgr = \frac{1}{2}Mv(d)^2 + 0 \end{align}\end{split}\]

Here’s another approach to what we’ve done so far:

Please answer Question 3 for points:

Words fail me