18.4. Isn’t Anything Constant??#
Wait. So, isn’t everything relative?
Glad you asked: So it would seem. But it’s not quite like that and what’s really important is actually what is always constant. That’s where Einstein’s frustrated university mathematics instructor comes in.
As we learned from the introduction to this lesson, in 1908 Minkowski put Special Relativity on a sophisticated mathematical foundation. His formulation first frustrated Einstein who grumbled:
“[about] superfluous learnedness…” “Since the mathematicians have grabbed hold of the theory of relativity, I myself no longer understand it.”
But he soon realized the importance of “invariance” in physics and made use of that notion many times later.
Invariance
Invariance: something that is unchanged under some “transformation.”
I want to hint at some pretty mathematics from 50,000 feet. The idea of a mathematical “transformation” is a very important idea and in fact governs modern physics in a deep way.
Suppose we have a square in front of us. A perfect, mathematical square. Let’s pretend that we can mark the corners to keep track of them as we play. But the numbers don’t do anything but guide the eye. Each corner is identical to the others.
A transformation is here a rotation of the square around its center, C.
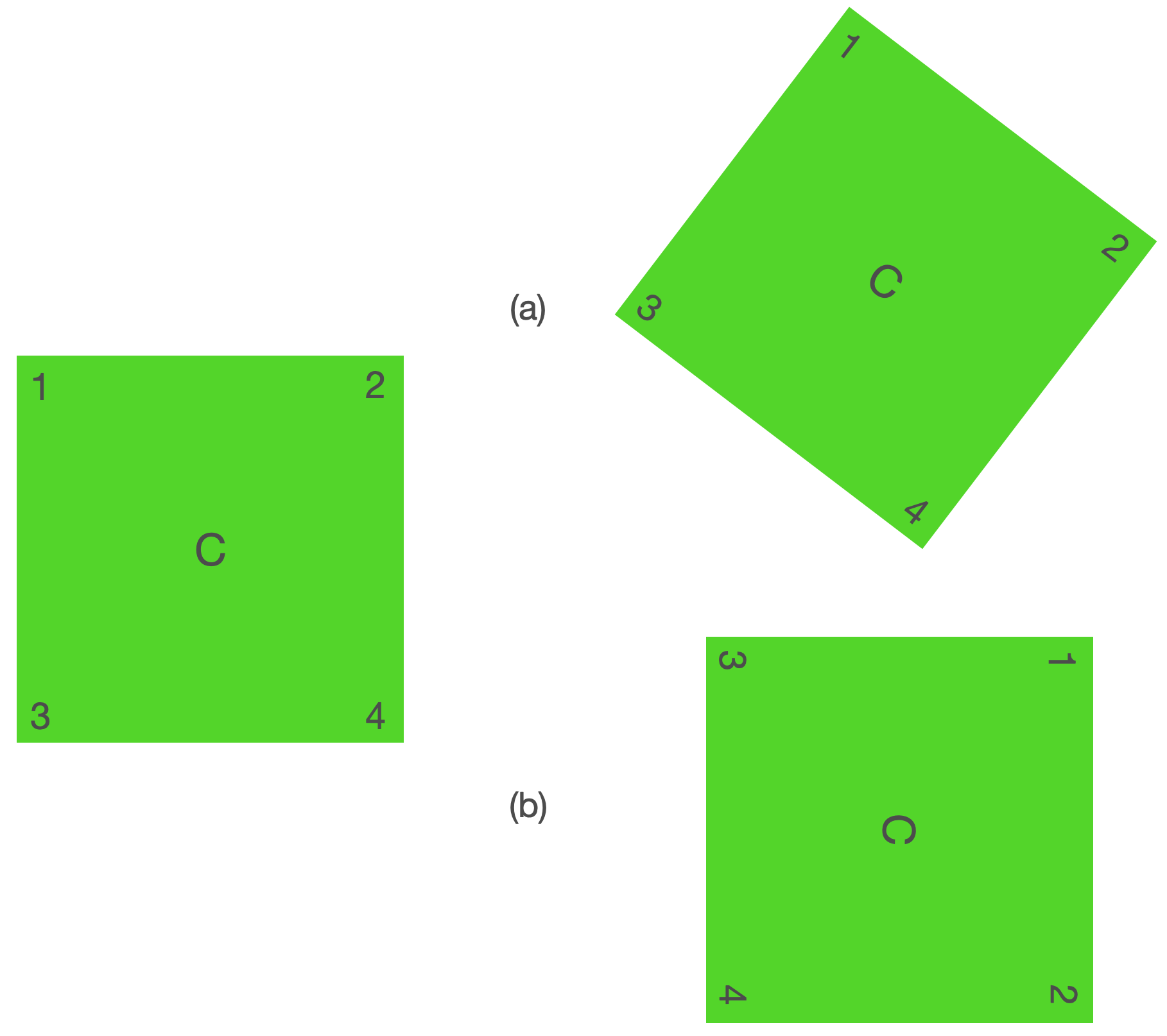
What kinds of transformations would leave the square “invariant”? That is, if I ask you to close your eyes and then I rotate the square around its center and ask you to open them, would you be able to tell whether it changed or whether it stayed the same?
If I did a rotation like (a) above, you’d say that the square was not the same. So we could conclude that a square is NOT invariant against a transformation of +45º about its center.
If I did a rotation like (b) above, you would not be able to tell that anything changed. Indeed, a square is invariant with respect to a transformation of 90º about its center. And 180º and 270º, 0º, and 360º. These are the only transformations that leave a square invariant.
Minkowski was an expert in the branch of mathematics called then, “Invariant Theory” and now “Group Theory” and he understood well that the manipulative description that I just gave could be constructed as math equations – functions – for which a transformation on the function leaves it unchanged in its form.
For example, remember that the equation for a circle is:
Suppose (in the same sense as you closing your eyes before the square manipulation) we transformed the \(x\) values that define the edge of a circle this way:
Every \(x\) becomes a minus \(a\). What is the new equation?
This has the same FORM as the original. It doesn’t matter what the variables are called. In this Group Theory game, what matters is the FORM of an equation. So a circle is invariant with respect to the transformation of its variables into their negatives.
18.4.1. Let’s Go to the Ballpark#
Have you ever thought about how major league baseball stadiums are laid out? No?
Seriously. Baseball parks?
Glad you asked: Stay with me. Invariance is afoot.
The MLB Rule Book says that…ahem:
Rule 1.04: “THE PLAYING FIELD: It is desirable that the line from home base through the pitchers plate to second base shall run East Northeast.”
Since baseball is not played in the morning, this orientation would minimize the likelihood that a batter would be staring into the sun. The advent of night baseball, indoor stadiums, and prevailing winds in various locations led to modern era baseball diamonds to be oriented in all sorts of different directions.
Here are two:
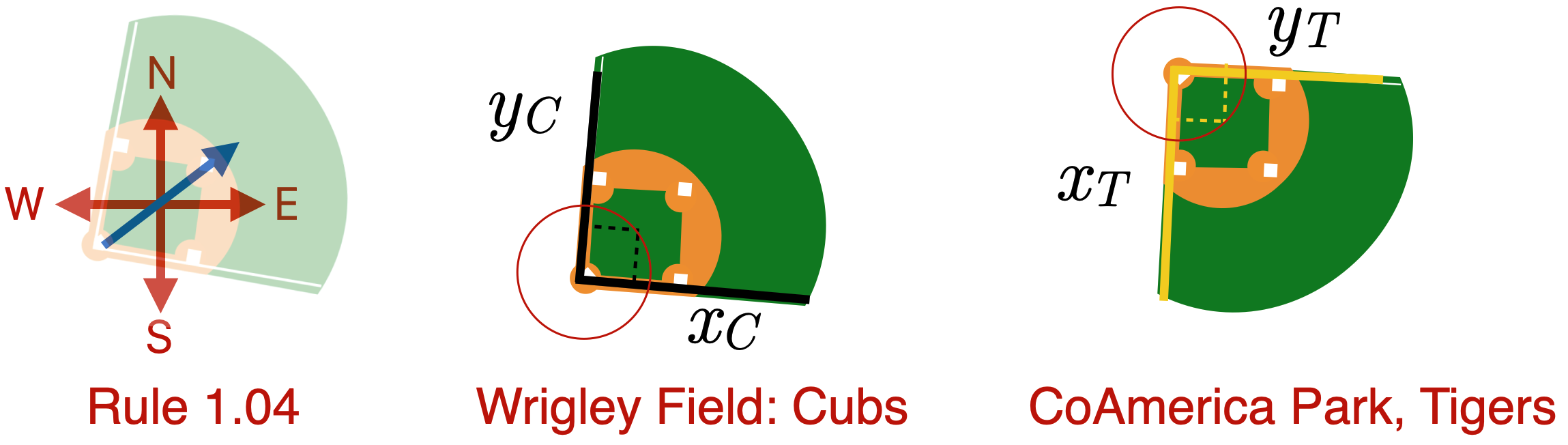
The left-hand figure is a picture of what the Rule Book demands and the elderly Wrigley Field in Chicago was constructed precisely that way, while the modern CoAmerica Park went its own way to accommodate its city streets. (Again, batters will face east, but southeast. Still no sun.)
Is everything relative in baseball? Well, no! The distance from home plate to the pitcher’s rubber is 60 feet, 6 inches in every ball park.[^pitcher]
There are so many strikeouts in the current game (2021) that there’s talk of taking some advantage away from the pitchers by lengthen the distance to the mound.
Notice in the figure above that there are two \(x-y\) axes drawn on top of each diamond, \(x_C-y_C\) for the Cubs and \(x_T-y_T\) for the Tigers. Notice too that a circle has been drawn centered on home plate – the origin of the two coordinate systems – in each of the parks. That circle has a radius of 60’ 6”.
Let’s write the formula that models that circle. There are two of them:
Clearly, these formulae look the same, and in the sprit of the above discussion it doesn’t matter what the names of the variables are, the form of the equations are identical. We would say that the length is invariant with respect to the choice of coordinate system since the \(L_P\) for each ballpark is the same 60’ 6”.
In a flat space of the sort you might have learned the geometry of in high school, for any number of coordinate systems, we could write:
where now the different coordinate systems are called 1, 2, or 3 and not Cubs, Tigers, Yankees…
This is very much like a well-worn example: Suppose a town hires two contractors to work on the creation of a set of streets in town. The first contractor uses magnetic north for his surveying jobs and the second contractor uses polar north for hers. The streets that they proposed to construct would be identical, street to street, corner to corner, house to house.
Let’s look at such a circle as described by three different coordinate systems.
That circle that’s traced out when the axes are aligned is called the Invariant Curve. You can see that an invariant length from your high school geometry class is represented by a circle.
What’s critical here is those plus signs. Any time that you find a length to be invariant and modeled by:
you know that you’re working in the high school geometry – called Euclidean Geometry – after the Greek mathematician who wrote the book that everyone learned from for 1500 years. Euclidean Geometry is the geometry that governs points, lines, and planes on a flat surface. This will become critical in Einstein’s future in more than one surprising way and we’ll draw the contrast more than once as we move through his work.
Here’s where Einstein’s frustrated math professor comes in. Let’s have a baby.
18.4.2. Minkowski’s Geometry#
What we’ve seen so far is that relativity is going to mix space and time.
We call the relativistic combination of space and time: Spacetime.
A natural question is what’s the “length” in space and time: Spacetime? What’s the invariant curve for relativity?
Note
What would that mean? It would be a way to describe an invariant interval as viewed from all possible reference frames. Following around the invariant curve would take you from Home to Away to another Away and another.
Let’s try the Euclidean Invariant curve for the “length” of space and time.
Note
Space and time are similarly dealt with so far, but they have different dimensions, right? Space might be measured in meters and time might be measured in seconds. Not the same. But we have a way around that. By convention we’ll use a “space” dimension for time by always multiplying t by c.
A proposal: We might guess that the “length” of a space and time interval (we use “\(\Delta s\)” to represent a spacetime interval) that the space and time coordinates would lead to a circle in Spacetime just like our “regular” space of ballparks and surveyors. For our “1” and “2” relatively moving coordinate systems, we might try
Seems reasonable, but let’s go to the hospital and think about what a Spacetime geometry of this sort might look like.
On the left of the figure below is then our proposal. (Notice that we can easily distinguish the future, with times greater than zero, from the past, where time would be negative given the choice of the origin.)
On the right is a “situation” for us to think about with that assumption.
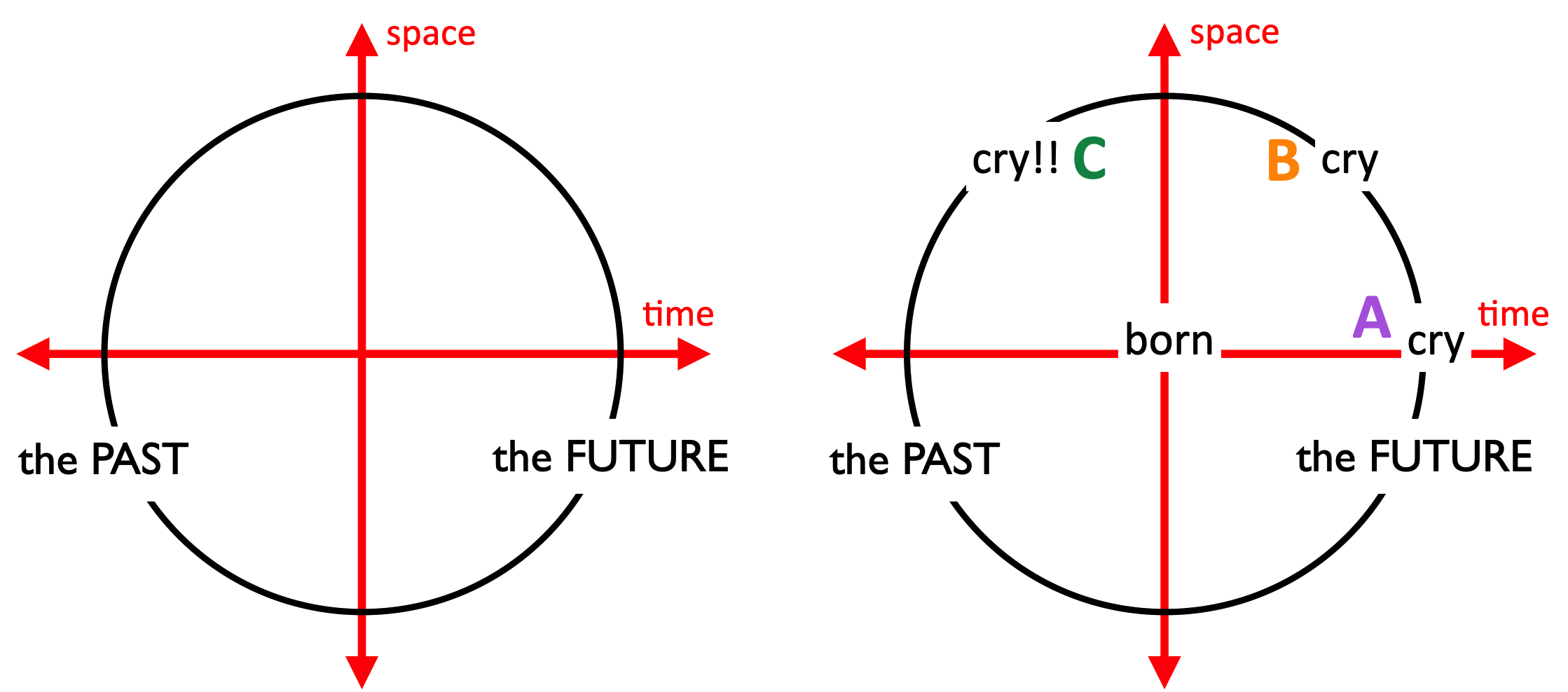
So we’re in the delivery room at a hospital. At the \(x=0\) point the newly born baby is first…well, born…and then some time later at that same space point, she cries, at the point labeled \(A\). Normal biological stuff. It’s a cause for celebration and little while later in time everyone in the family cries.
Suppose we’re driving by the hospital and somehow (don’t ask how) we observe that same blessed event. Now as time progresses, so does our distance from the origin, so we all agree that the baby is born at the origin but we see the first cry at point \(B\), since we’ve moved in our frame. That’s maybe not too hard to imagine.
Now we drive by in a different direction – a different frame, that Special Relativity should be able to describe. We again see the baby born at the origin but uh-oh. Before the birth, the baby cries. If the circle is the space and time invariant curve then the rules of relativity should work for all points on the curve – this proposed circle.
But that’s not how births happen! The first crying event for every newborn is after, not ever before, the birth. We have to conclude that the Euclidean circle is not the invariant curve for Special Relativity. In the abstract, this is not just a silly example, it implies a violation of cause and effect. Where an effect seems to happen before its cause. Not good.
While the maternity ward was not on Hermann Minkowski’s mind, he did figure out the correct kind of geometry to describe events in Special Relativity. It was a new geometry that he invented and today we call the space in which that geometry functions, Minkowski Space.