14.2. Wave Goodbye#
While the idea of an electromagnetic wave will change as we move into the late 20th century, there are some basic notions of waves that we’ll need. First doesn’t it make sense that we can think that all substances in the macroscopic world are either particles – or collections of particles – or waves.
Let’s think in terms of basics: the obvious features that distinguish particles and waves. It’s useful to think of idealized examples: an ideal particle will be one that’s infinitesimally small while an idealized wave extends in infinite directions and is perfectly repeating.
So, what is the most characteristic feature of a particle? That’s easy: Particles have a place, a definite location in space – it’s here. And furthermore, when it’s here, it’s also not simultaneously there. But a wave is everywhere, all the time. You can’t get much more different than that. It sounds almost like a distinction that only Aristotle could make, even if true.
But there are also tenuous similarities. Particles carry kinetic energy and transmit it through collisions with other particles. So too a wave is a disturbance that transmits energy. The tremendous destruction of a tsunami is terrible evidence of how energy can be imparted by waves. But the difference here is that the actual constituents of the wave don’t themselves translate but they stay put. This figure shows a finite disturbance like in a guitar string.

A “pluck” of a string transmits the potential energy of the displacement of the particles in the string through the tension and relaxation of the string. The disturbance moves away, while the bits of string stay put.
If you pluck a stretched string, you’ll create a disturbance that will actually move down the length of the string at a predictable speed where it would stop, or reflect and come back. If the string is attached to a bell clapper, it would ring. Obviously, energy and momentum have been transferred from your fingers through the string, sufficient to ring the bell.
Remember this:
Waves transmit energy.
It will be useful to think of waves as simple “sine waves.” That’s a simplification.(We will see later that any such non-repeating shape can actually be built up by a set of infinite sine waves of different wavelengths.) It’s also useful to contrast two kinds of waves: Longitudinal and Transverse.
Longitudinal Wave: A wave in which the disturbance is along the direction of motion.
Transverse Wave: A wave in which the disturbance is perpendicular to the direction of motion.
Longitudinal waves are compressional, like a slinky toy and appear in nature most readily in the propagation of sound. When a noise is made, the noisemaker vibrates and leaves a momentary compression or rarefaction in the surrounding air – a local high or low density region. This back and forth of high and low densities moves outward as the propagating sound wavefront. Actual molecules of the air don’t follow the wave all the way to your ear – local air molecules move and affect adjacent air molecules and that hand-off-disturbance is what propagates.
You eventually hear the sound, because that disturbance eventually reaches your ears and bangs on your eardrum like…a drum. Here is a cartoon showing two positions of a compressional disturbance along a spring-like substance.
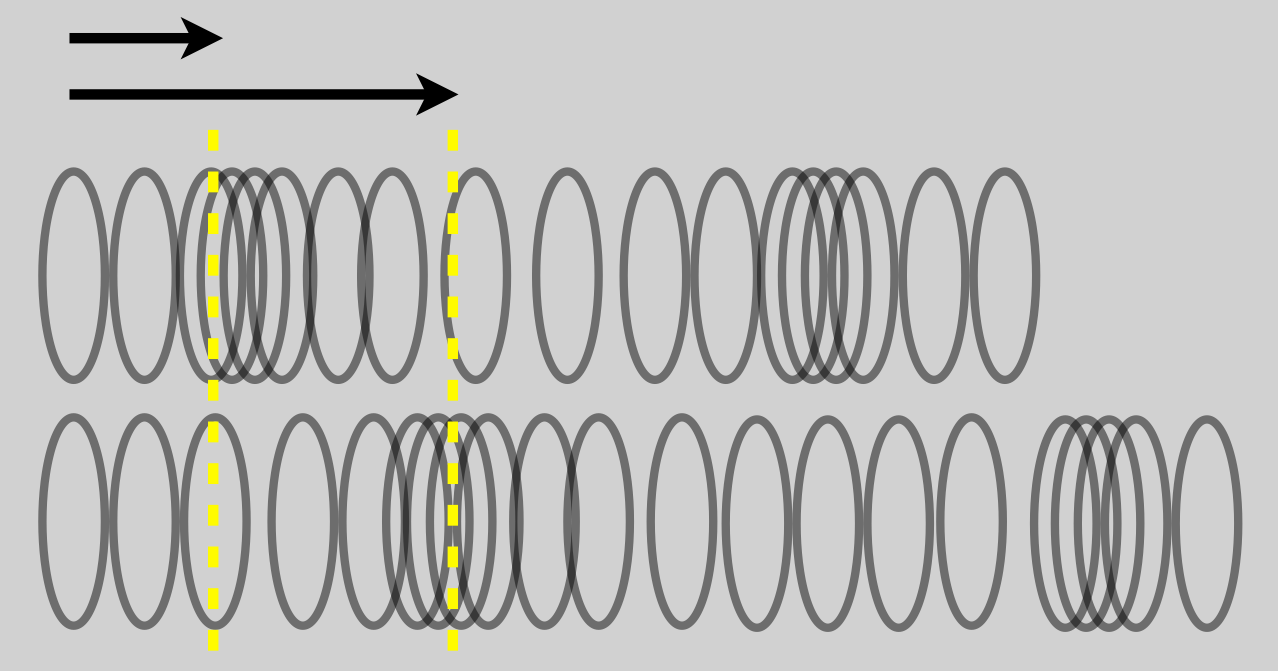
This is a longitudinal wave with the disturbance moving along the direction of the “slinky” and in the same direction as the speed of the wave.
Transverse waves are different in that the disturbance is not in the direction of the propagation, but perpendicular to it (that’s the definition of “transverse”). Water waves are the simplest example. If you toss a stone into a lake, the disturbance is the water going up and down but the wave propagates “outward” from the source in concentric circles. Again, the actual molecules of the water don’t move outward with the wave, the water molecules move up and down and affect adjacent water molecules through the tension in the water’s surface rubber ducky just bobs up and down, he doesn’t follow the wave. This is a typical, infinite transverse wave. This figure shows a typical (infinite) transverse wave.
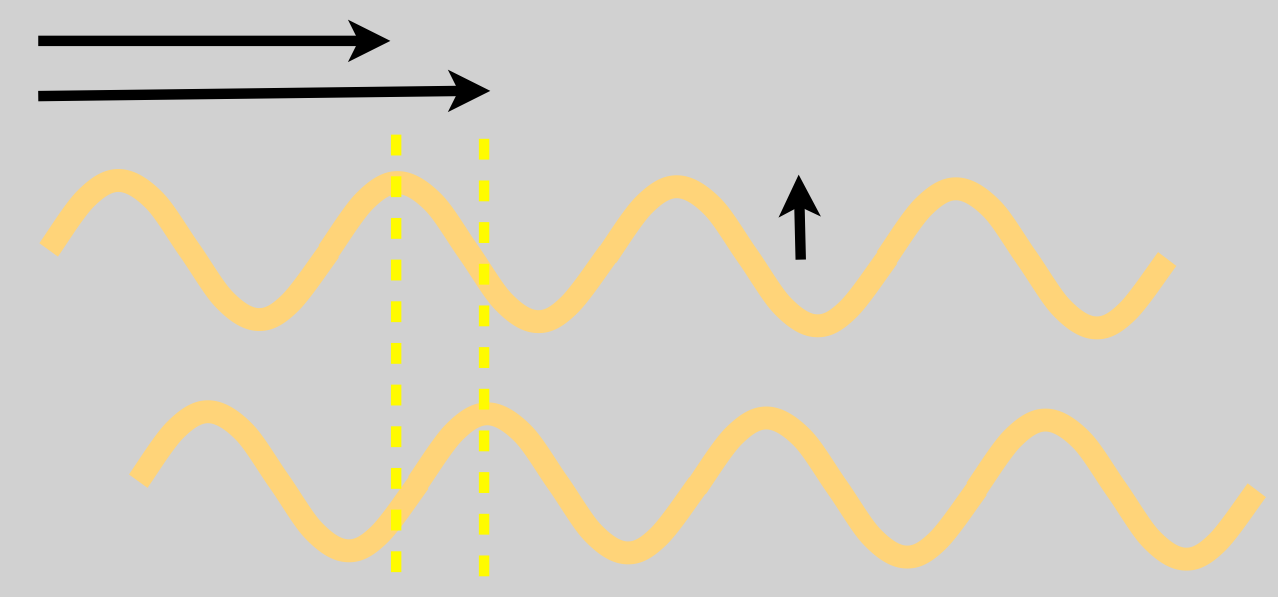
This is an example of a transverse wave where the disturbance is up and down but the propagation of the wave is along the length perpendicular to the disturbance, hence “transverse.” Notice that each peak (and valley…and every point in between) has moved to the right between the top and bottom snapshots of the wave.
14.2.1. Wave Parameters#
We can characterize a moving sine wave with only a few parameters, which are are familiar from everyday life: frequency, wavelength, and amplitude. Notice that a wave is oscillating in space – you see the water wave undulate where the peaks are all in a pattern outward from the disturbance. But also a water wave oscillates in time where each point on the surface of the water is rising or falling in rhythm with all of the other points on the surface. That means we could plot the wave as either a pattern in space or time and the functional description of a wave would contain \(x\) and \(t\) variables.
The next two figures show these two circumstances with three important features of waves indicated on each.
Representation as a function of distance, highlighting the wavelength:

As a representation over distance, the disturbance varies with distance in a periodic way and the length of that repeating distance is the ” wavelength,” \(\lambda\).
Representation as a function of time, highlighting the frequency:
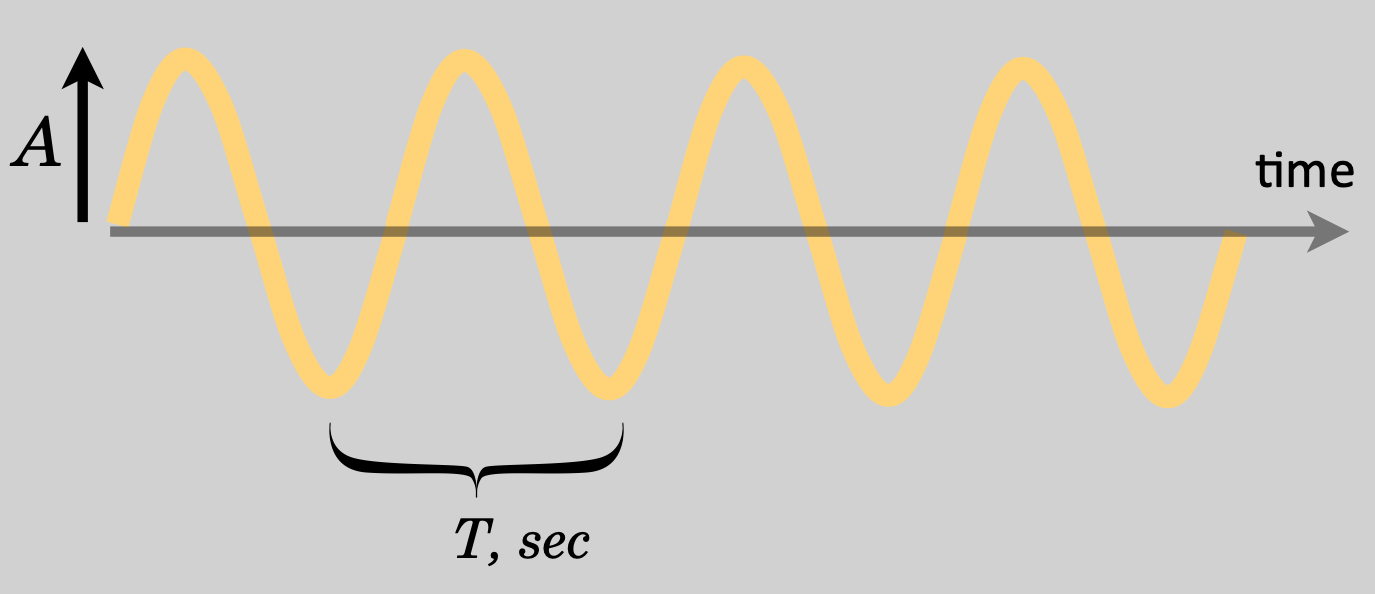
As a representation in time, the disturbance varies in time in a periodic way and the duration between points that repeat is the ” period,” \(T\).
The two most obvious parameters in the space picture are:
wavelength, which is the distance in space units between any two equivalent values of the disturbance along the length of the wave (using the Greek letter, lambda \(\lambda\)) and
amplitude, \(A\), the maximum disturbance which can be a length (like the height of water waves) or related to other measurable parameters like the value of pressure or light intensity or other not-so-obvious quantities like for electric and magnetic fields.
In the time picture there are also two obvious parameters:
period, usually represented as \(T\)—which is the time that it takes for any same value of the amplitude to repeat (which is measured in seconds) and
amplitude, the same amplitude as in the space picture!
The most common wave parameter – it’s on every radio dial – is the frequency which is the rate at which the wave repeats: the number of repetitions per unit time which has the units of \(s^{-1}\) or “per second.” This is given the name Hertz (Hz), after the great German physicist who first detected electromagnetic waves, Heinrich Hertz (1857-1894). House electrical current in the United States is a sinusoidal shape (alternating current, or “AC”) with a frequency of 60 Hz, or 60 cycles per second.
I’ll use the symbol \(f\) for frequency, although it’s also commonly represented as the Greek letter \(\nu\). (I don’t want to create any confusion with \(\nu\) for frequency and \(v\) for velocity.) Obviously, if the rate that the wave changes is \(f\) (“cycles per second”)and the time interval between the changes is \(T\) (“seconds per cycle”), then:
The space and time representations of the pictures of waves are connected by the actual speed of the wave (which makes sense since speed connects space and time!). This connection is the important relation (\(v\) is velocity!),
Here are all of the parameters and their relations:
With this introduction, let’s now see the light:
14.2.2. The Speed of a Wave#
The speed of a wave depends on the medium, its density, temperature, structure, and so on. But, to first approximation, the wave speed doesn’t depend on the wavelength or the frequency (or the amplitude), so if the frequency goes up for some wave (like sound) because the speed stays the same, the wavelength goes down. High frequencies mean smaller wavelengths, and visa versa.
Get used to \(c\):
The symbol \(c\) is reserved for that very special speed of light.
Electromagnetism is special. And this will be the rub for a really young Albert Einstein. The speed of electromagnetic waves in a vacuum is always (Here “always” will become a surprise.):
Wait. You’re always doing that: hinting at something to come.
Glad you asked: Yup. It’s a narrative trick, I guess. So many properties and features of nature were completely upended, that it’s fun to get you settled into something that’s comfortable and sensible and then rhetorically pull the rug out from under you later.
Please study Example 1 🖋 📓
Our concern will be with the “electromagnetic spectrum” and here it is in its full glory:
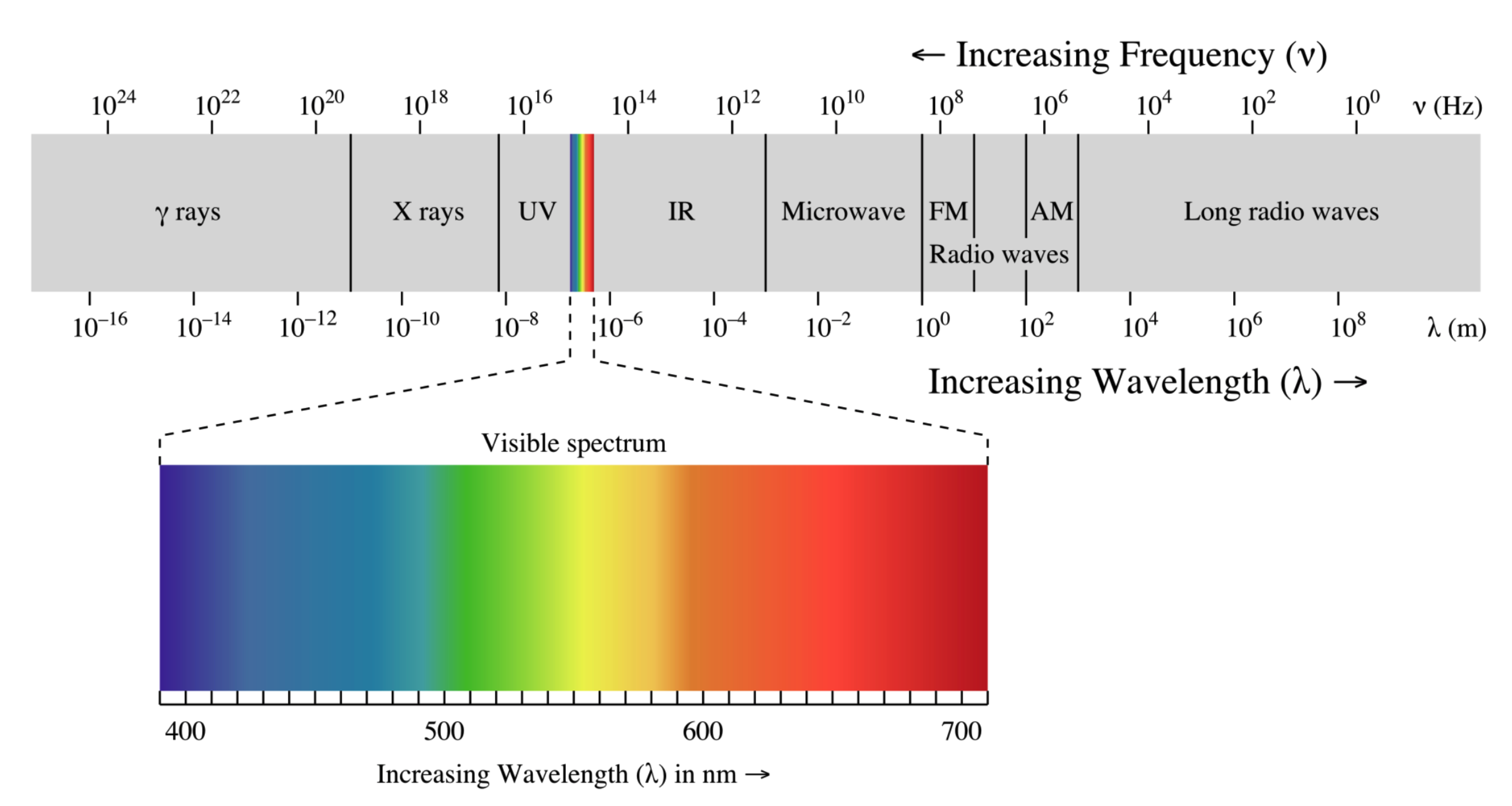
There are many phenomena that you have undoubtedly heard of and maybe didn’t realize we’re all the same thing. X rays, gamma rays, infrared rays, radio waves, and of course visible light waves…only differ by their frequency or by their wavelengths.
Electromagnetic waves all move at \(c\) so they can be characterized by either their frequency or their wavelengths. Notice that I wrote “rays” and “waves” which correspond to their everyday usage. This respects the history of their discovery as well see.
Wait. There you go again.
Glad you asked. \(\star\) crickets \(\star\)
Wait. There you go again.
Glad you asked: \(\star\) crickets \(\star\)