6.8. Finally, Nothing: Forces in Balance

We’ve been dealing with Newton’s 2nd law as if there’s only one object and one force, but what it really says is more general (but where the mass remains constant):

\[\begin{split}\begin{align*} \text{add up all forces on an object } &= ma \\ F_1+F_2+F_3 + \ldots & =ma \end{align*}\end{split}\]

Here are three example situations:

The left figure imagines a single force with no friction, like pulling a sled on smooth ice. The middle figure assumes that Mo is pulling the sled across grass, so there’s friction. The right figure imagines that Ossie is sitting on the sled which makes the friction more and adds to the overall mass. Notice the relative lengths of the two friction forces, with and without the added Ossie-load.

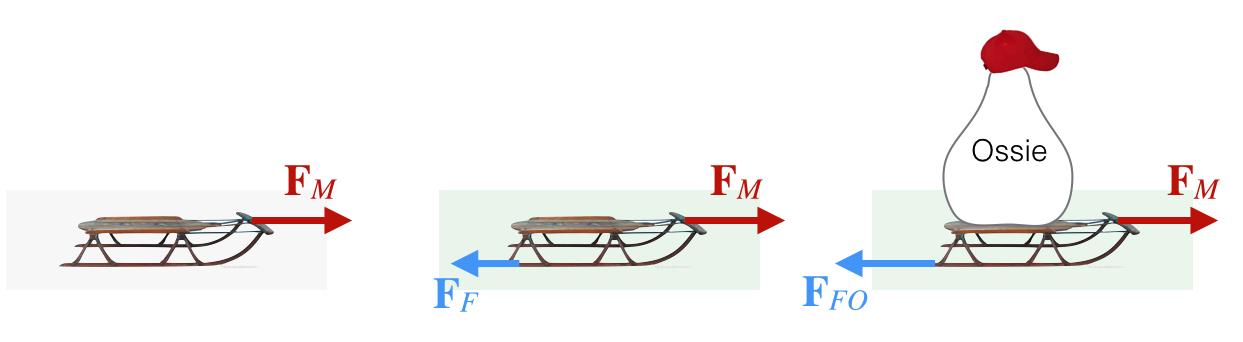
The simplest example: Mo is pulling his vintage wood & cast-iron Mickey Mouse Flexible Flyer sled across a frozen pond. He’s a strong guy and he can apply a pretty steady force, which we’ll call \(F_M\). In that case, while he pulls, he’s working out the acceleration in his head:

\[ F_M=m_Sa_S \nonumber \]

He pulls with \(F_M\), the sled has mass \(m_S\), and the sled accelerates at \(a_S\). Mo, while book-brainy is not too everyday-smart.

While he enjoys sledding in the winter, it’s too cold during that time so he prefers to do his sledding during the summer. In order to get to his favorite hill, he has to drag his sled across the grass. Carefully calibrating his force again, he pulls at the same value of \(F_M\) but doesn’t achieve the same enthusiastic acceleration as on the ice because of the friction which is responsible for a force that points in the opposite direction, \(F_{F}\). Now his acceleration is

\[ F_M-F_F=m_Sa_S \nonumber \]

So clearly the sled’s acceleration is less than in the cold months. The value of the frictional force, \(F_F\), depends on how hard the sled is pressed against the grass and scales just about evenly with the mass of the sled.

Mo’s friend Ossie prefers to not walk and so he rides on the sled and so the mass that Mo needs to work against is that of the sled plus Ossie, \(m_S+m_O\). Ossie presses the sled into the grass more so its frictional force, \(F_{FO}\), is also more and it just balances Mo’s steady, determined force, \(F_M\), so \(F_M=F_{FO}\), or:

\[\begin{split}\begin{align*} F_M-F_{FO} &=(m_S+m_O)a_S \\ F_M-F_{FO} &=0 \end{align*}\end{split}\]

So when the forces balance, there’s no acceleration. When there’s no acceleration, the speed doesn’t change. So can Mo still get to his warm hill? Why yes, if he got the sled up to some speed (say Ossie doesn’t get on until it’s moving) then it will continue at that speed, which is another way to say that it does not accelerate. Which is another way to say Newton’s 1st law is at work.

You already have an intuitive feel for this force-balancing act. Because, tug of war:

  Pens out!

tug of war

  Please answer Question 6 for points:

more tug of war