4.4. A Gentle Review 1: Skills You’ll Frequently Need

There are three levels of math refresher in this lesson:

1. This section: skills that you’ll use a lot during the semester. Please familiarize yourselves with these topics and read seriously until you see the stop sign: 🛑

2. Skills that you’ll use only a few times. Skim this. Know that it’s there, but don’t dig in now unless you want to.

3. Some boutique skills that might be necessary only once. Just know that they’re there.

You might find it useful to brush off some previous skills that we’ll need to make progress. I have in mind simple algebra, exponents, powers of 10, and some simple geometry formulas.

4.4.1. Some Algebra Practice

I’ll show you some examples of the level of algebra we’ll need, but let’s first pause and salute the most important thing about algebra:

The Fairness Doctrine of Algebra: If you do something to one side of an equation, you must do the same thing to the other side.

Words to live by. Armed with this, here we go. You’ll be surprised how simple this will be.

Wait. It’s been a long time since I took algebra. I don’t like where this is heading.

Glad you asked. Can you sing or play an instrument? You can read music and glean meaning and insight from playing music…but I’ll bet you’ve not composed music. I want to use mathematics in that spirit. I’ll ask you to play along — read algebra — but almost never will I assess your progress in QS&BB by asking you to compose — derive — mathematical arguments.

Here’s a representative list of the kinds of mathematical thinking I’ll ask you to be able to read:

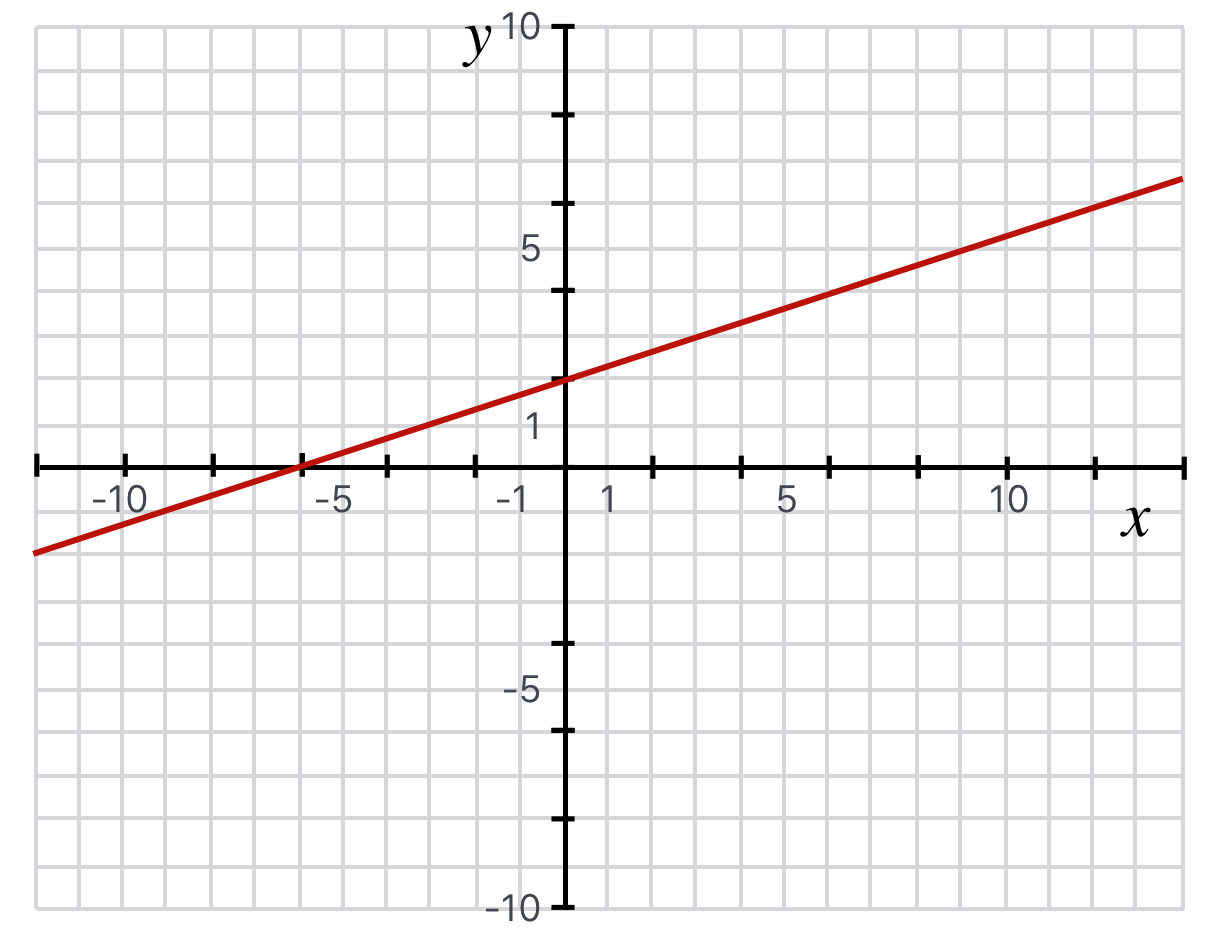
1. \(y=mx + b\) presents four parameters — symbols that stand for something. For this example, I’ll define \(b\) and \(m\) as constants. A numbers… like “3.” The \(y\) and \(x\) are variables and have a particular one-to-one relationship that comes from the context: the value of \(y\) depends on the value of \(x\). \(y\) is the dependent variable and \(x\) is the independent variable. We would say that “\(y\) is a function of \(x\).”

  Pens out!

A question! In symbols, can you solve this equation for \(x\) as a function of \(y\)?

Glad you asked. Yes.

Bad job! That’s not what I meant and you know it.

Glad you asked. Be specific. Here’s how I’d do that, and I’ll insert every step even though you might do some of them in your head:

\[\begin{split}\begin{align*} \text{work out the strategy to isolate $x$:} \;\;\; y &= mx+b \\ \text{get rid of $b$ on the right:} \;\;\; y - b &= mx +b - b \\ y-b &=mx \\ \text{get rid of $m$ on the right:} \;\;\; \frac{y-b}{m} &= \frac{mx}{m} \\ \frac{y-b}{m} &= x \\ \text{just rearrange it in order ot admire the result:} \;\;\; x &= \frac{y-b}{m} \end{align*}\end{split}\]

Good job! “Function” is a 100-dollar word but really just an algorithm…a machine: put in an \(x\) and you get out a \(y\). That’s all a function does.

Now, let’s solve that equation.

  Pens out!

A question! If \(b=3\) and \(m=0.5\), what is the value of \(y\) if \(x=8\)?

Glad you asked. I’d put in the values and do the calculation:

\[\begin{split}\begin{align*} y &= mx + b \;\;\; \text{ always set the stage by starting at the beginning} \\ y &= (0.5)(8)+3 = 4+3 = 7 \end{align*}\end{split}\]

Good job!

Now. Maybe you recognize this particular equation…remember from somewhere in your life the sentence: “y equals mx plus b”? The equation for a straight line.

All equations can be graphs—-that’s from the brilliance of primarily Rene Descartes as you’ve read above. But let’s plot it and see how to solve it graphically:

$y=0.5 x + 3$. The dot is the result of graphically \"solving\" the equation when $x=8$.

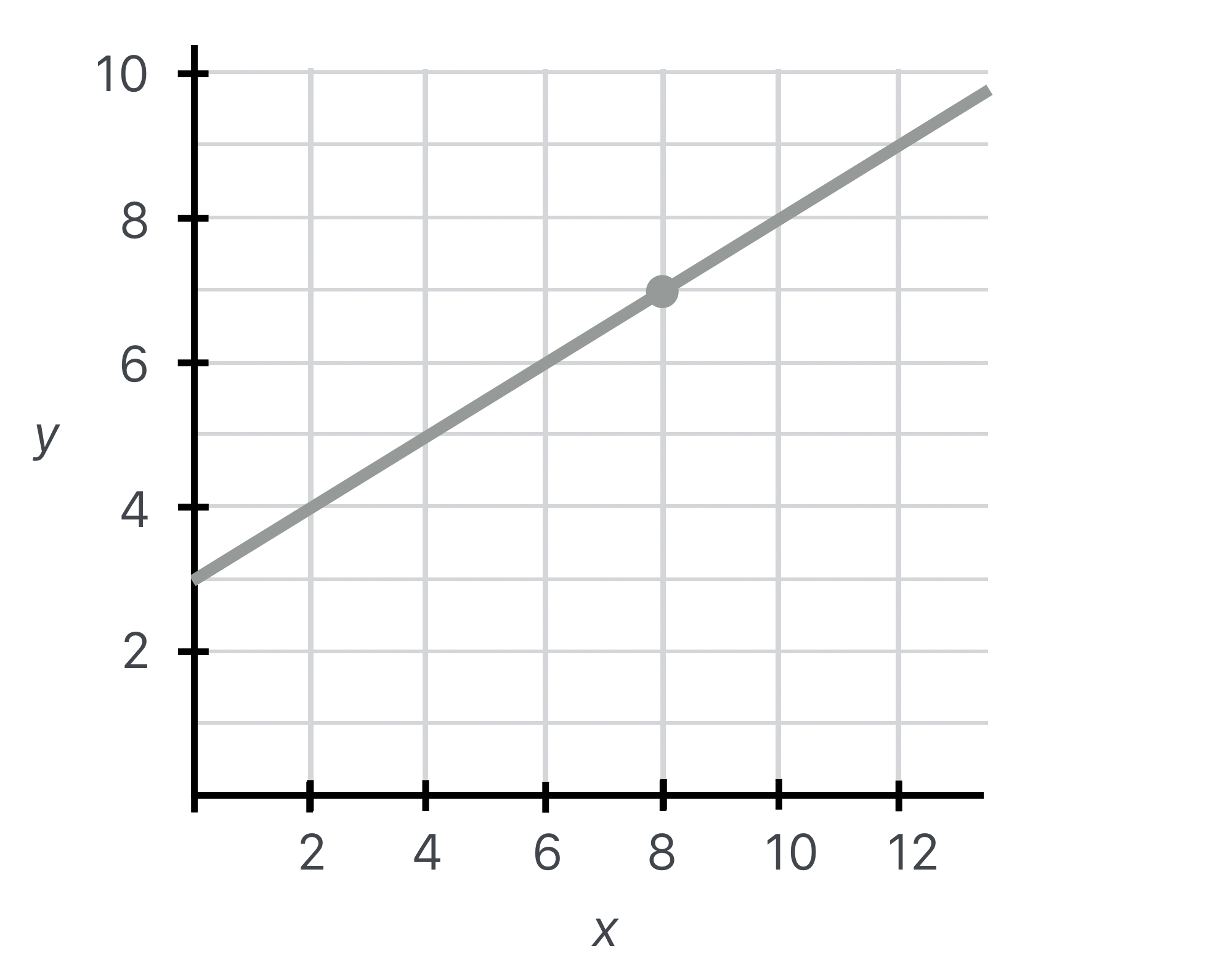
You can see that plugging in the numbers into the formula gives the same result as plotting the function and evaluating it at particular points.

My intention in QS&BB is to tell as much of the story of particles and cosmology as I can, but without undue mathematical complexities. I’ll want to refer to very complicated functions, but I’ll plot them. Just like this simple function. Then to “solve” those complicated equations…we’ll just read the graph. The dot above is a visual “solving” of the equation as you saw.

Reading a graph is the same thing as solving an algebraic formula. If you can do that, you can do a lot of complicated physics.

2. We will need the occasional square root and exponent. Let’s remind ourselves of a simple manipulation. One more example:

  Pens out!

A question! In the equation \(c = \frac{1}{\sqrt{a+b}},\) can you solve for \(b\)? Wait. I mean: Please solve for \(b\).

Glad you asked. ;) Sure. I’ll do it like before, annotating each step:

\[\begin{split}\begin{align} \text{start from a clean beginning:} \;\;\; c &= \frac{1}{\sqrt{a+b}} \\ \text{make the square root disappear:} \;\;\; c^2 &= \frac{1}{a+b} \\ \text{get $b$ upstairs:} \;\;\; c^2(a+b) &= \frac{1}{a+b}(a+b) \\ c^2(a+b) &= 1 \\ \text{work to isolate $b$:} \;\;\; \frac{c^2(a+b)}{c^2} &= \frac{1}{c^2} \\ a+b &= \frac{1}{c^2} \\ b &= \frac{1}{c^2} -a \end{align}\end{split}\]

Good job!

It will be no more difficult than this.

Our appetite for algebraic complexity will be very modest. We’ll not encounter formulas that are much more complicated than these. Please (please) convince yourself that you can do the solutions in the right hand column.

  Pens out!

\[\begin{split}\begin{align} y &= a\times x = ax \quad &\text{ solve for x to get}\quad x &=y/a \\ y &= x + z \quad &\text{ solve for x to get}\quad x&=y-z \\ y &= a\times x + b = ax + b \quad &\text{ solve for x to get}\quad x&= \frac{y-b}{a} \\ y & = \sqrt{ a+x} \quad &\text{ solve for x to get}\quad x &= y^2 -a \\ y & = \frac{b}{\sqrt{ a+x}} \quad &\text{ solve for x to get}\quad x &= (\frac{b}{y})^2 -a \end{align}\end{split}\]

(Were you writing? I’ll wait.)

Can you do each of these? Then you’re good: that’s about all that you’ll need to remember of algebra. Just remember the rule. Then…it’s merely a game—a puzzle to solve.

4.4.2. The Powers That Be: Exponents

Instead of “\(y^n\)” some of you might have learned to write: “\(y\)^\(n\).” I’ll stick with my way and I hope you do also.

Once in a while, we’ll need to multiply or divide terms that have exponents, including powers of 10. There are simple rules for this, but let’s figure them out by hand…so to speak. The first thing to remember about exponents is that in a term like \(y^n\), a positive integer \(n\) tells you how many times you must multiply \(y\) by itself. So: \(y^1 = y .\) Here, there’s just one \(y\).

  Pens out!

The second thing to remember is that \(y^0 = 1\). There aren’t any \(y's\) in the product and so all that could be there is 1. Armed with that, let’s kick it up a notch.

Suppose I have \(y\times y\). You’d be pretty comfortable calling that “y-squared” and from the above, the number of \(y's\) there are in that product is two. So \(y\times y = y^2.\) If I add another product, then I’d have \(y\times y \times y = y^3.\) Get it? Notice that what we’ve also got in this equation is: \(y\times y \times y = y^2 \times y^1= y^3\) and we’ve just developed our first rule on combining exponents:

\[y^n \times y^m = y^{n+m}.\]

  Pens out!

Question! What is \(x^2x^1x^4\) ? Glad you asked. \(x^2x^1x^4=x^{2+1+4}=x^{7}\) Good job!

One more time, but different. Another rule recalling that a negative power means “one over…”:

\(x^{-n} = \frac{1}{x^n}.\)

If the same rule for adding exponents works — and it does — then we can multiply factors with powers by keeping track of the positive and negative signs of the exponents.

So here’s an easy one: \(\frac{x\times x \times x}{x\times x} = x\) which you quickly get by crossing out two \(x\)’s in the numerator and the denominator leaving you with one left over.

Or, by using the powers and the rule:

\[\frac{x\times x \times x}{x\times x} = \frac{x^3}{x^2} = x^3 \times x^{-2} = x^{3-2} =x.\]

Now you try it.

  Please answer Question 1 for points:

practice with exponents

One more thing. The powers don’t have to be integers.

Perhaps you’ll remember that square roots can be written:

\[\begin{split}\sqrt{x} &= x^{0.5} = x^{1/2} \\ \mbox{so:} & \\ \sqrt{9} & = 3 \;\; = \; 9^{0.5} \\ \mbox{or:} & \\ \sqrt{\frac{1}{9}} & = \left(\frac{1}{9}\right)^{0.5} = \sqrt{frac{1}{9} = \frac{1}{9^{0.5}} = 9^{-0.5} \\ & = \frac{1}{3} \end{split}\]

4.4.3. Formulas from your past that might be explicitly useful

I know that you’ve seen most of this somewhere in your past! So return with us now to those thrilling days of yesteryear. Straight lines, circles, and the areas and circumference of circles and triangles are useful.

4.4.3.1. Equation of a straight line

A straight line with a slope of \(m\) and a \(y\) intercept of \(b\) is generally described by the equation,

\[y = mx+b\]

A straight line with a slope of $1/3$ and a $y$ intercept of $2$, so $y=\frac{1}{3}x+2$.