17.4. Speeds in Special Relativity#
What we’ve seen so far is that space and time intervals between two relatively moving inertial frames of reference are…unusual. Remember our Weary Traveler on the airport sidewalk, just standing there while the sidewalk moves? He’s not taking advantage of the opportunity to get to where he’s going faster than if he were walking. That’s not what the sidewalk is for!
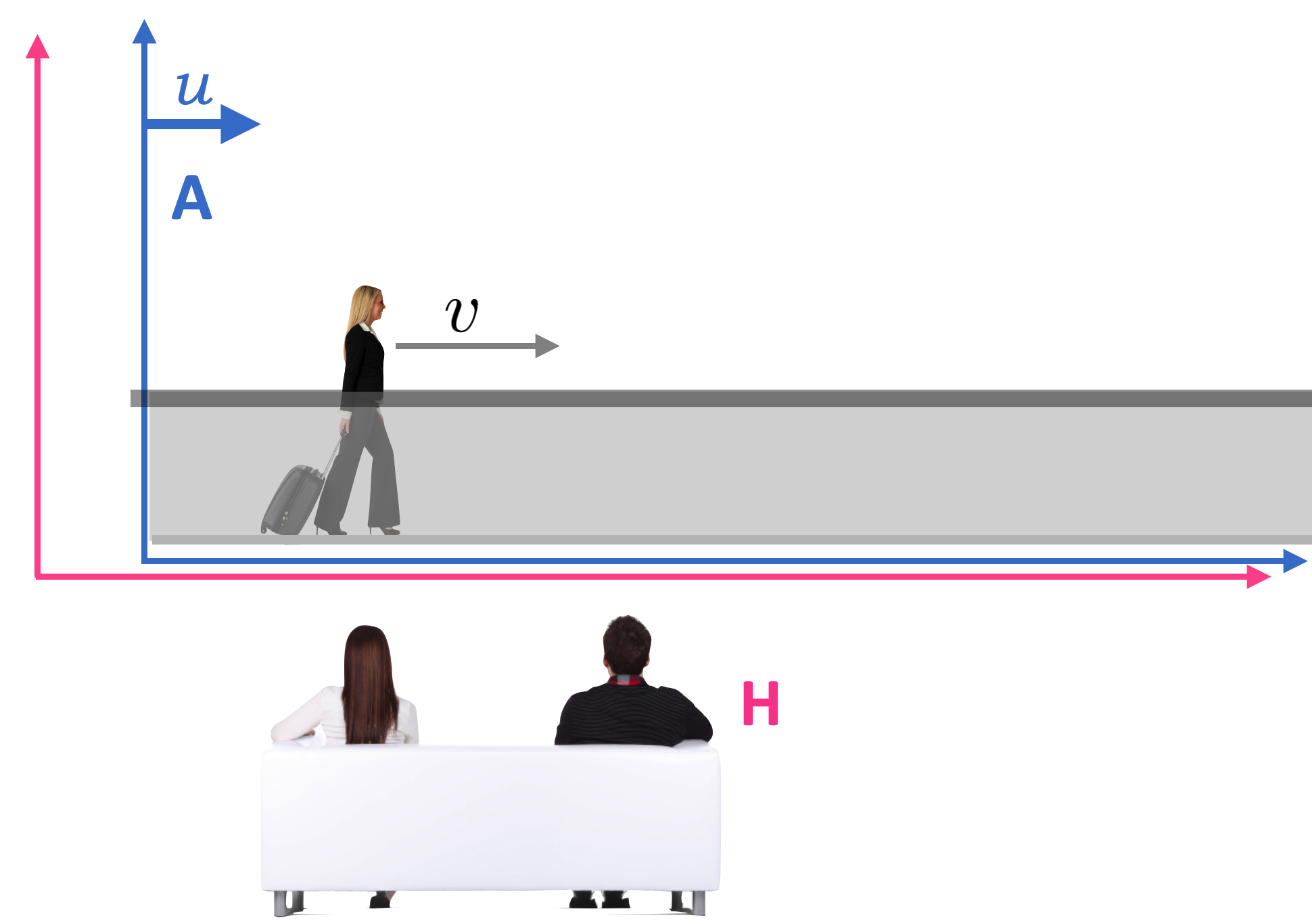
A more experienced traveler would hop on the moving sidewalk and then walk on the moving sidewalk. If one could walk at 2 m/s relative to the sidewalk, and if the sidewalk itself moves at 3 m/s, wouldn’t you speed through the airport at 5 m/s?
Pencils Out! 🖋 📓
Let’s keep our designation of the relative speed of a reference frame as \(u\) and use the symbol \(v\) to represent the speed of an object inside of the Away frame. Then that simple, common-sense calculation in the previous paragraph would be
But think about what the Home frame observer would see. If there’s movement in the Away frame, then speed there would be
But as viewed in the Home frame, both the numerator and the denominator are bound to be different than what Newtonian mechanics would suggest. In that “classical” world-view, the \(\Delta t\) term would be the same regardless of what reference frame we’re in and just dividing the transformed \(x_H = ut + x_A\) by that classical, invariant speed, \(\Delta t\) would give Equation XXX above.
But now we know that not only space transforms but also time transforms as determined in two different inertial frames, so our simple \(2+3=5\) calculation can’t be correct in Relativity.
The actual determination involves calculus and so I’ll just tell you the result. You’d expect to see \(c\) in there, right? And you’d not be disappointed.
It looks complicated, but let’s do what we always do in a relativistic equation: what does it look like if \(u\) is very, very small relative to \(c\)?
So we get back the Newtonian result as a slow-frame approximation of the relativistic form.
We can play another game here. What if the moving object in the Away frame is a beam of light? That is, if \(v_A=c\)?
Please study example 2 🖋 📓
So the Second Postulate falls out of this equation. If \(v_A=c\), then \(v_H = c\) also.
Let’s divide everything by \(c\). We’d get:
This is a relation that’s dimensionless and doesn’t depend on any particular speed, just how it relates to the speed of light. So let’s plot \(\dfrac{v_H}{c}\) versus \(\dfrac{v_A}{c}\) to see what happens:
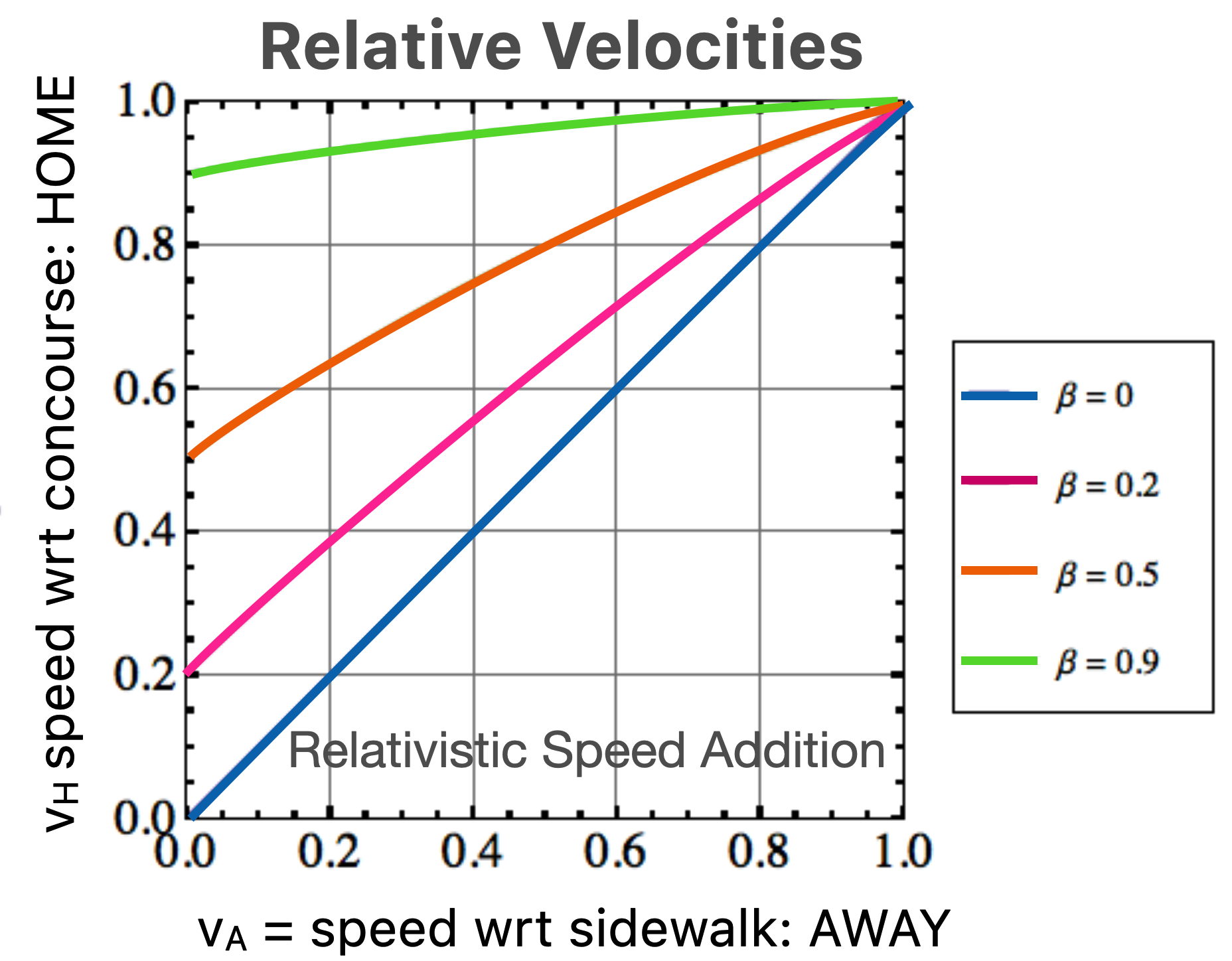
So remember, we’ve got three different velocities going on here. Let’s use this plot:
Note
Suppose we have a frame of reference that’s moving at half the speed of light relative to another frame, so \(\beta=0.5\). If an object is moving at \(0.4c\) in that Away frame, then how fast is it moving in the Home frame?
In the Newtonian picture, you’d have said \(0.9c\), right? Here’s what that would look like.
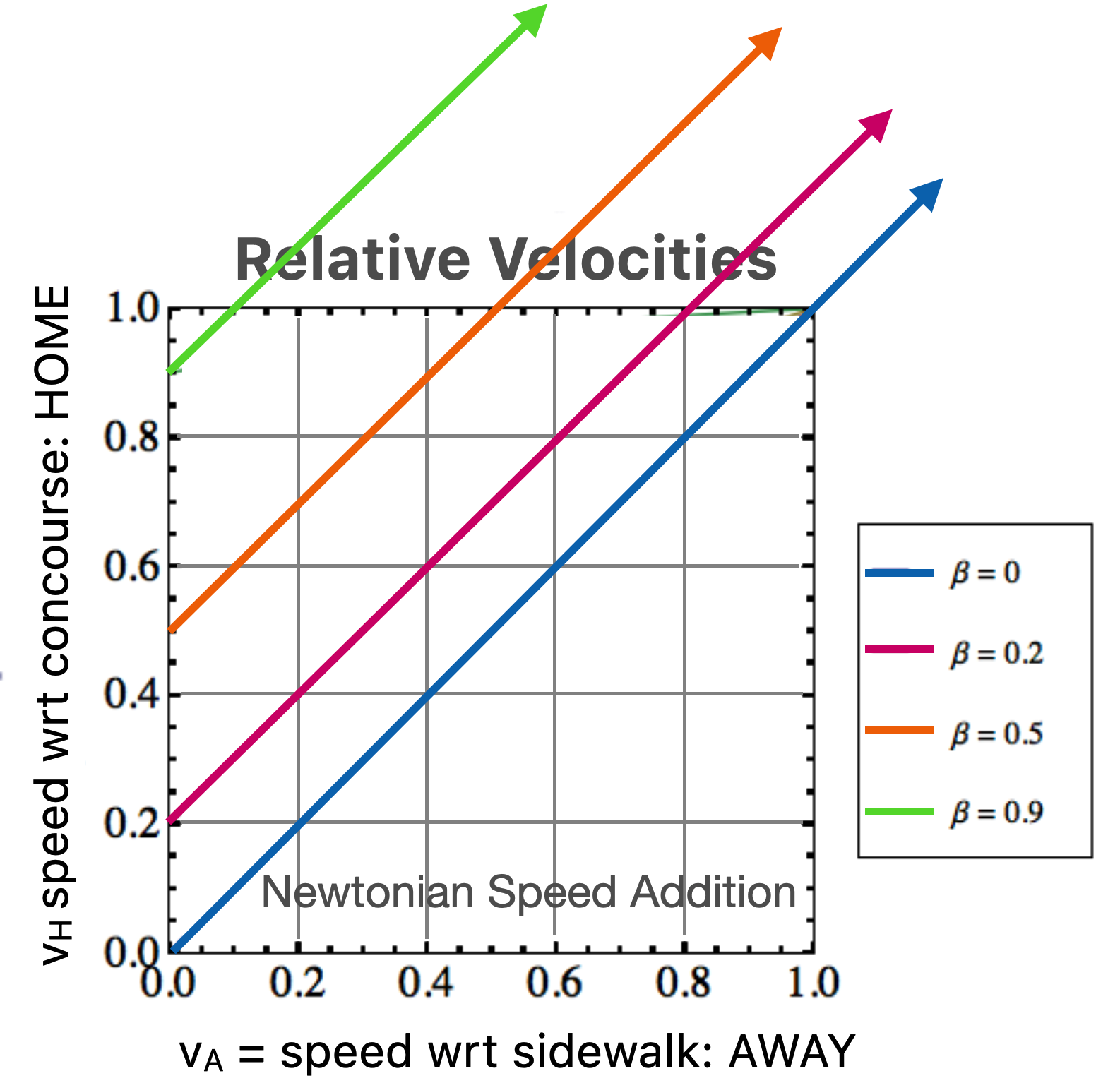
However, in relativity, it’s a different story and we can use the formula or look at the graph to get that result. From either we’d estimate that it would be moving at about \(0.7c\) or so.
Note
Here is an interactive plot that you can use to find the speed transformation for any value of \(beta\). Click “Run” and you can then mouse over the plot and read off the values of \(v_A\) and \(v_H\).
Remember to push Run:
Please study example 3 🖋 📓
Please answer question 2 📺
Notice also that the curves for the Relativity speed addition turn over as \(u\to c\), while the Newtonian speed addition results are unbounded. That’s a hint that the speed of light is a limiting velocity. More about this in a bit.
17.4.1. Interstellar Space Travel#
The closest solar system to ours is near the star Alpha Centauri a little more than 4 light years from Earth.
Note
Remember that a “light year” (aka ly) is the distance that light would travel in one year. It’s:
Note
That’s a hike.
In the sky, near the Southern Cross, is a tiny red dwarf star, Proxima Centauri, which is 4.23 light years from us. It has a planet that is about 1.2 times the mass of Earth, Proxima Centauri b, which is in the habitable zone of its star. That means that liquid water could exist on “Planet b.”
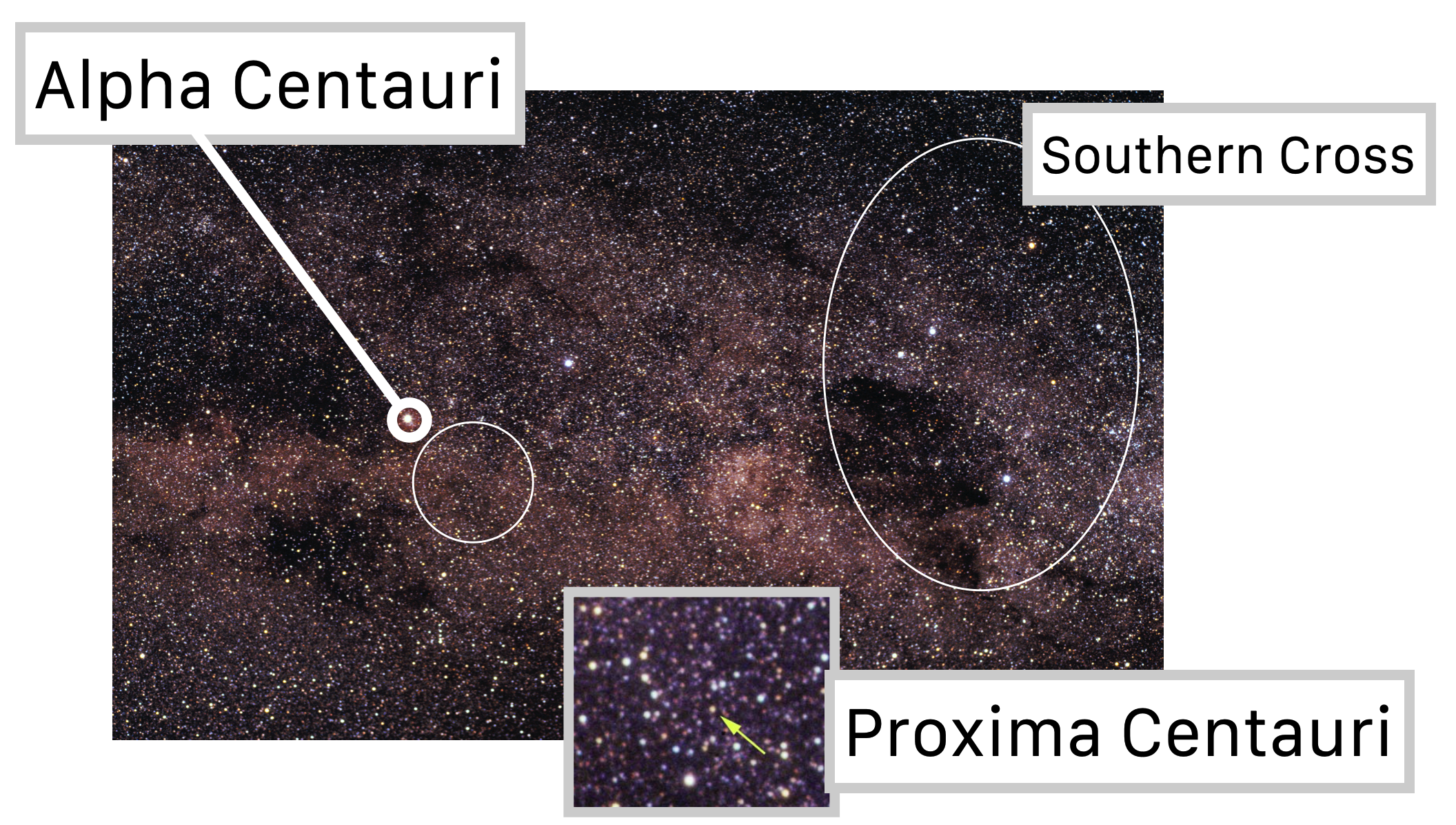
At this writing, in 2021, 4 years ago means that for any of the TV-watching residents on Planet b, Will has just disappeared from the quiet town of Hawkins in Stranger Things since it took four years for that first episode to travel from, Earth to Proxima.
How might humans get there? I’d refer to the great science fiction novel, Tau Zero, by Poul Anderson. It’s a great story and full of relativity. The “tau” refers to the proper time, which remember we represent as \(\tau\) rather than \(t\). Remember, that’s the special time that’s inside of a Home reference frame. It’s the time you see on your watch. In the story, space travelers have propulsion sufficient to power their craft at a constant acceleration of \(g\), so on board, it seems like Earth gravity. That’s an enormous acceleration and it’s not clear how that could ever be achieved given the fuel required. But let’s run with it. Or rather, fly with it for fun.
Remember that Newton would have said that the speed that a spacecraft would achieve at a constant acceleration of \(1g\) would be
Simple, right? The relativistic version of this is a little more complicated and I’ll not solve it for you algebraically, but I’ll “solve” it for you as a graph. The easiest way to show this is not a specific speed, but plotting \(\beta =v/c\) as a function of time, in this case, days of acceleration.
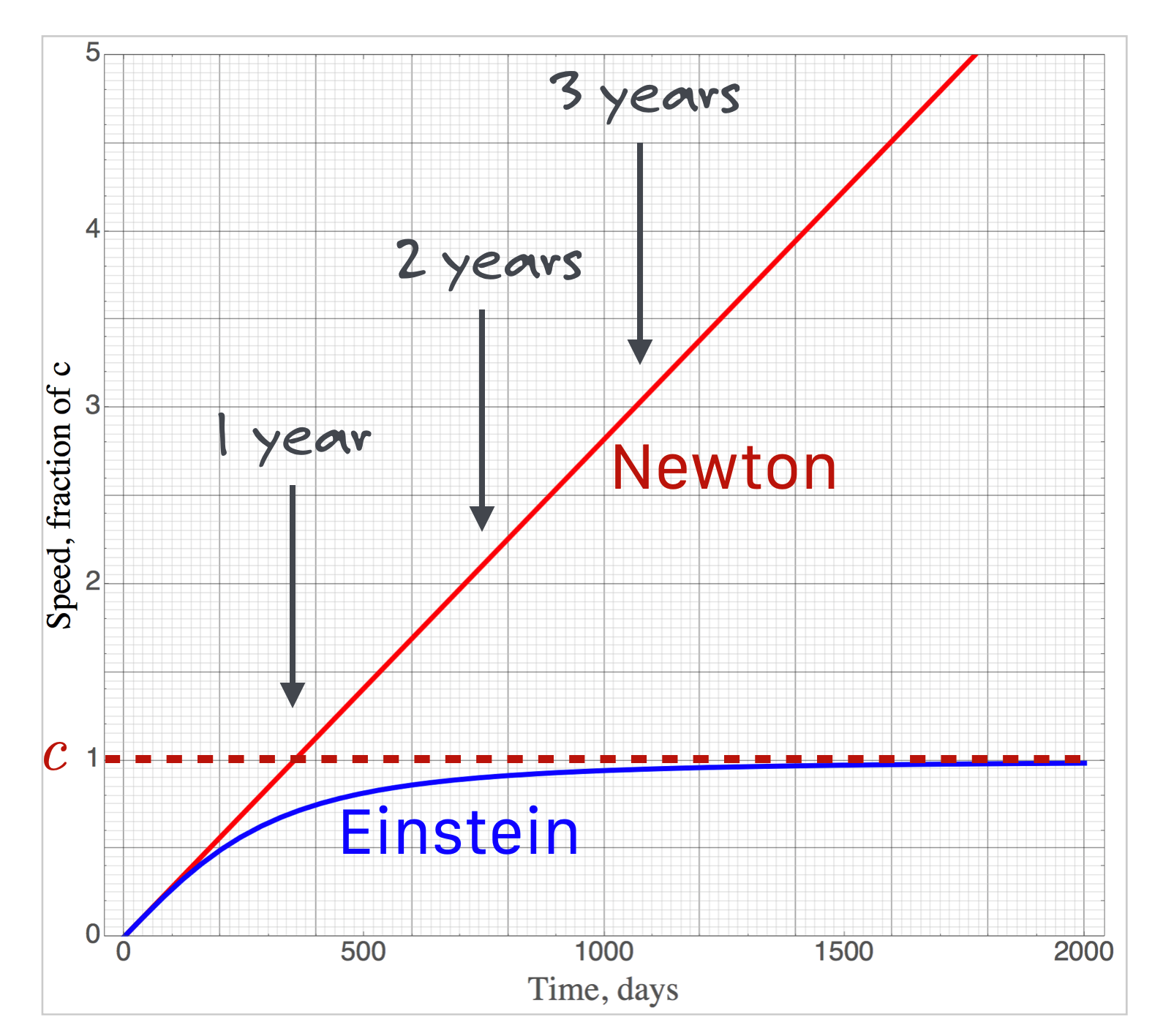
Newton’s acceleration just increases without bound, but look at what happens in a relativistic world: the speed is limited to always be less than the speed of light. In the first half a year or so, the Newtonian and relativistic speeds would be pretty much the same, but then they start to separate. After a year of this acceleration, the (real, relativity-observing) spacecraft would be traveling at about 75% of the speed of light, while the Newtonian speed would just be crossing the speed of light on to faster and faster, fictitious(!) velocities.
What does this mean for a trip to Proxima Centauri? Here again, the mathematics is formidable so I’ll just show you the results of my calculation. We need a strategy since we don’t want to be constantly speeding up…we have to slow down to arrive! So here’s the flight plan:
We’ll accelerate at \(g\) for two light years,
cruise at whatever speed that takes us to for 0.2 light years, and
then we’ll decelerate at \(-g\) for two light years.

The top speed as viewed from the Earth is \(0.9453c\) which is also the speed that the Earth is moving away from the spacecraft.
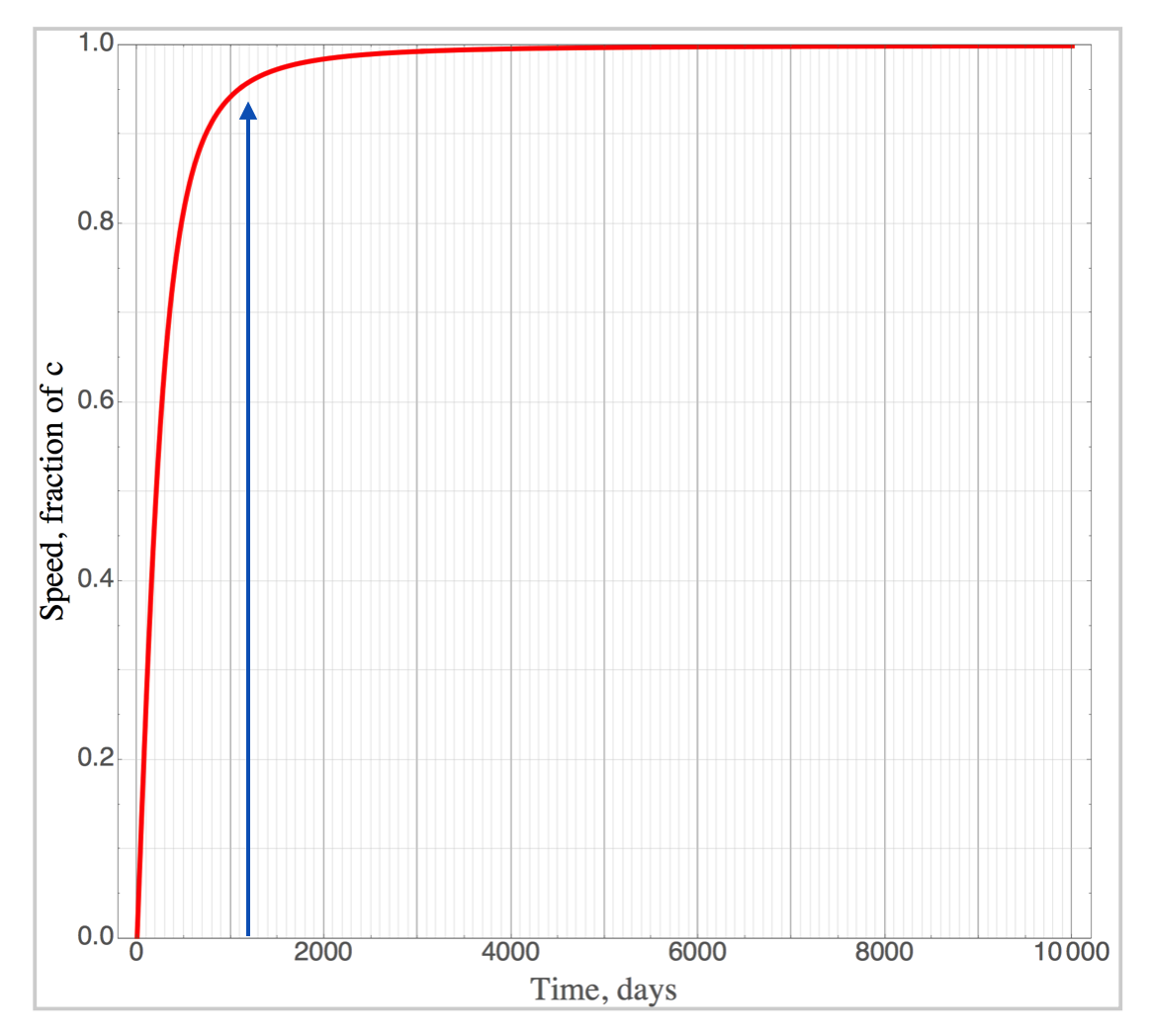
Some fun facts about this trip:
acceleration time, relative to Earth = 2.8 years
acceleration time, relative to ship = 1.7295 years
whole trip time, relative to Earth = 5.8695 years
whole trip time, relative to ship = 3.5428 years
The graph above is from the perspective of the spacecraft. This is a graphic (no pun intended) picture of Time Dilation for a “modest” trip within our neighborhood.
Let’s do it one more time. Think Star Trek. Trappist-1 is a dwarf star that’s 40 ly from Earth. Let’s go there with the same propulsion system and a similar flight plan:
We’ll accelerate at \(g\) for nine light years,
cruise at whatever speed that takes us to for 22 light years, and
then we’ll decelerate at \(-g\) for nine light years.
Here’s how that would go. Changing lives and families, both on-board and on Earth.
acceleration time, relative to Earth = 9.9 years
top speed, relative to Earth = 0.9953 c
acceleration time, relative to ship = 2.97 years
whole trip time, relative to Earth = 41.9 years
whole trip time, relative to ship = 8 years
Note
You might be wondering about this accelerating frame of reference and whether Special Relativity can handle that? That’s a tricky thing and involves the mathematical feature of a frame being “inertial” instantaneously. At each step along the way, the speed of the frame is increasing, but at each step, that frame can be considered inertial. In General Relativity, which we’ll deal with in a bit, all frames are relative, while in Special Relativity, ostensibly only inertial frames are relative. The big difference here is that our rocket travels at a constant acceleration, which is more restrictive than a General Relativity perspective where everything is relative. Sorry. This is one of those things that’s pretty deeply embedded in mathematics that we’re not going to dig into in QS&BB.
17.4.2. Inertia?#
Look back at the previous two figures. The relativistic increase of speed with time is not linear like it would be for Newtonian dynamics. Think about this. We’re applying a constant force but not getting back a constant speed. We go faster, but at a slower rate. It’s as if we’re moving through an increasingly resistive medium…like cement that gets more and more dense as we go.
Suppose we’re walking along and as we go someone is adding weight to our backpack. The more massive we get, the harder it is to maintain our speed. What’s happening is that just from a simple-minded \(F=ma\): our inertia appears to be increasing.
Those curves are a hint that something like the inertia of the spacecraft is increasing, the faster we go. What’s the measure of inertia? Mass.
Time for the T-shirt equation.