Relativity 3

Relativity 3#

Example 3: Full Pion Decay#

The Question: Back to the decay of the unstable particle called the “pion” (\(\pi\)). It decays in a chain into another unstable particle called the “muon” (\(\mu\)) and while we considered it before, we really didn’t follow the muon that it decays into: $\( \pi \to \mu + \nu \to e + \nu + \nu \nonumber \)$ All we did before was consider the “clock” of the time that it takes the pion to decay on average. Now we’re going to follow the muon itself before it in turn decays further.

We didn’t consider any motion for the muon but what really happens is that the pion decay provides kinetic energy to the muon and so while it’s born in the pion’s Away frame, it then moves in the pion’s Away frame.

So the question is if we watch this in our Home (lab) frame, how fast to we see that muon moving?

The scenario:

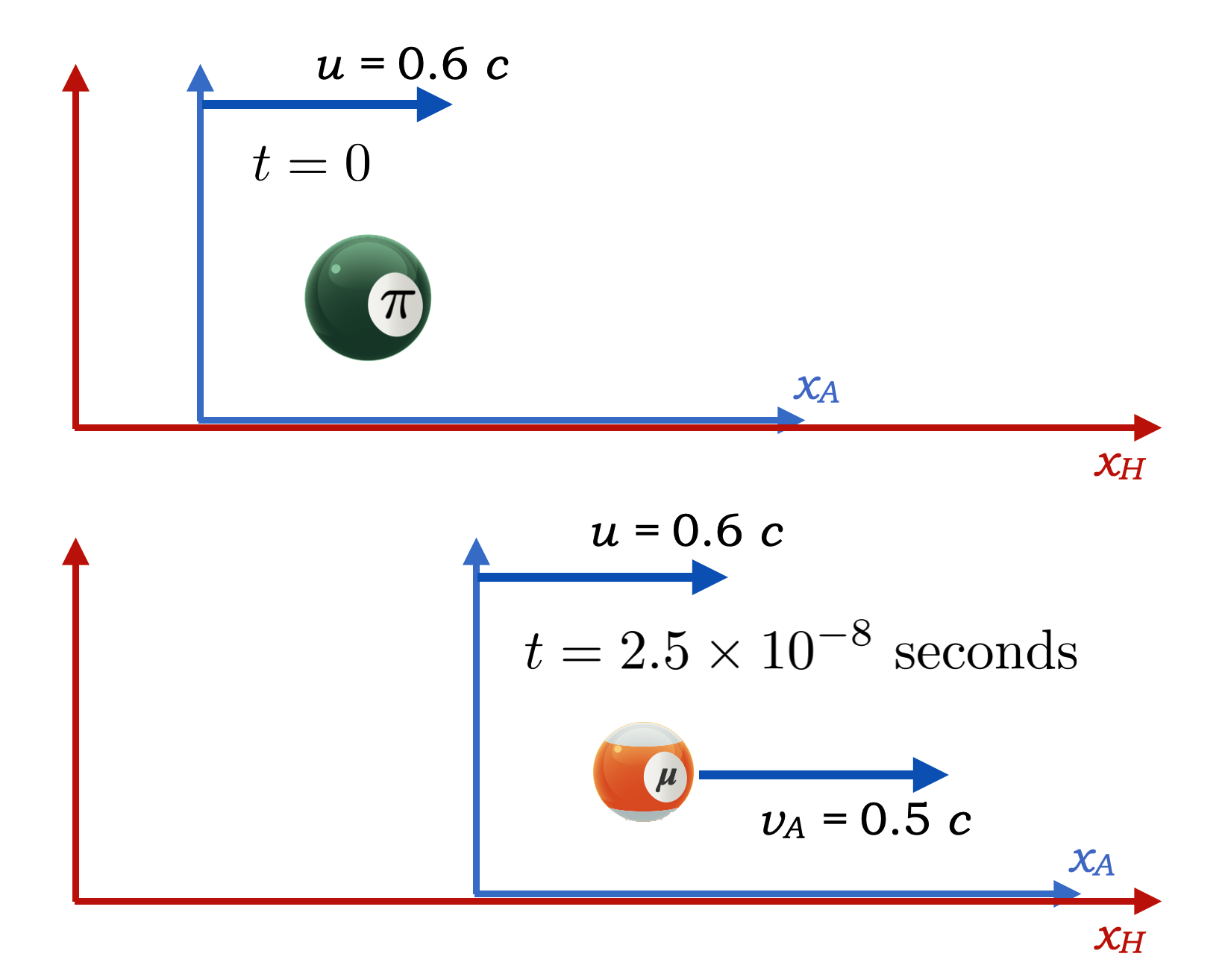
  • A pion is produced in an accelerator and moves away from its place of birth at a speed of half that of light. The pion is itself its own rest frame (the “proper frame”)

  • The lab in which it was produced is where we are observing. So the lab is Home and the pion’s frame is Away and is moving at \(u=0.6c\).

  • The pion decays into a muon after one of it’s lifetimes of \(2.5 \times 10^{-8}\) seconds. So we have a distinct interval: the pion is born and then the pion decays. It’s a little clock with one “tick” and never a “tock.”

  • The muon itself is born and moves away from the point in space where the pion decayed with its own kinetic energy, and hence, velocity. We’ll say that’s \(v_A = 0.5\times c\).

How fast does the muon appear to be going as observed in the lab, Home, frame?

galilean_train

The Answer:

We need to keep track of the \(v's\) and \(u's\).

  • \(u=0.6c\) for the pion’s frame…our Away frame

  • \(v_A = 0.5c\) as the muon’s speed inside of the Away frame

  • \(v_H\) would be the speed of the muon in the lab, or our Home frame: what we want to determine

Notice that if this were a Galilean analysis, then

\[ v_H = v_A + u = 0.5c + 0.6c = 1.1c \]

…which we know can’t be the case!

The model says that (where I’m naming the particles):

\[ v_H(\mu) = \frac{v_A(\mu) + u(\pi)}{1+\dfrac{v_A(\mu)u(\pi)}{c^2}} \nonumber \]

So we can solve this in two ways. We can use the interactive graphic in the lesson to read the answer right off. By characterizing the speeds as fractions of \(c\) we’re ready to do that straightway. We’re just saying, where the quantities are the x and y axes of the figure:

\[ \dfrac{v_H}{c} = \frac{\dfrac{v_A}{c} + \beta}{1+\beta \dfrac{v_A}{c}} \nonumber \]

Or, we can easily plug into the formula:

\[\begin{split} \begin{align*} v_H(\mu) &= \frac{v_A(\mu) + u(\pi)}{1+\dfrac{v_A(\mu)u(\pi)}{c^2}} \\ v_H(\mu) &= \frac{0.5c + 0.6c}{1+\dfrac{0.5c \times 0.6c}{c^2}} \\ v_H(\mu) &= \frac{1.1}{1+0.3} \\ v_H(\mu) &= 0.85c \end{align*} \end{split}\]
Contents