Relativity 2

Relativity 2#

Example 2: Length Contraction#

The Question: Length contraction is a more difficult thing to wrap your head around and practical example of it are harder to conjure up. You’ll read about one in the text.

Let’s run with a ruler (not scissors).

The scenario:

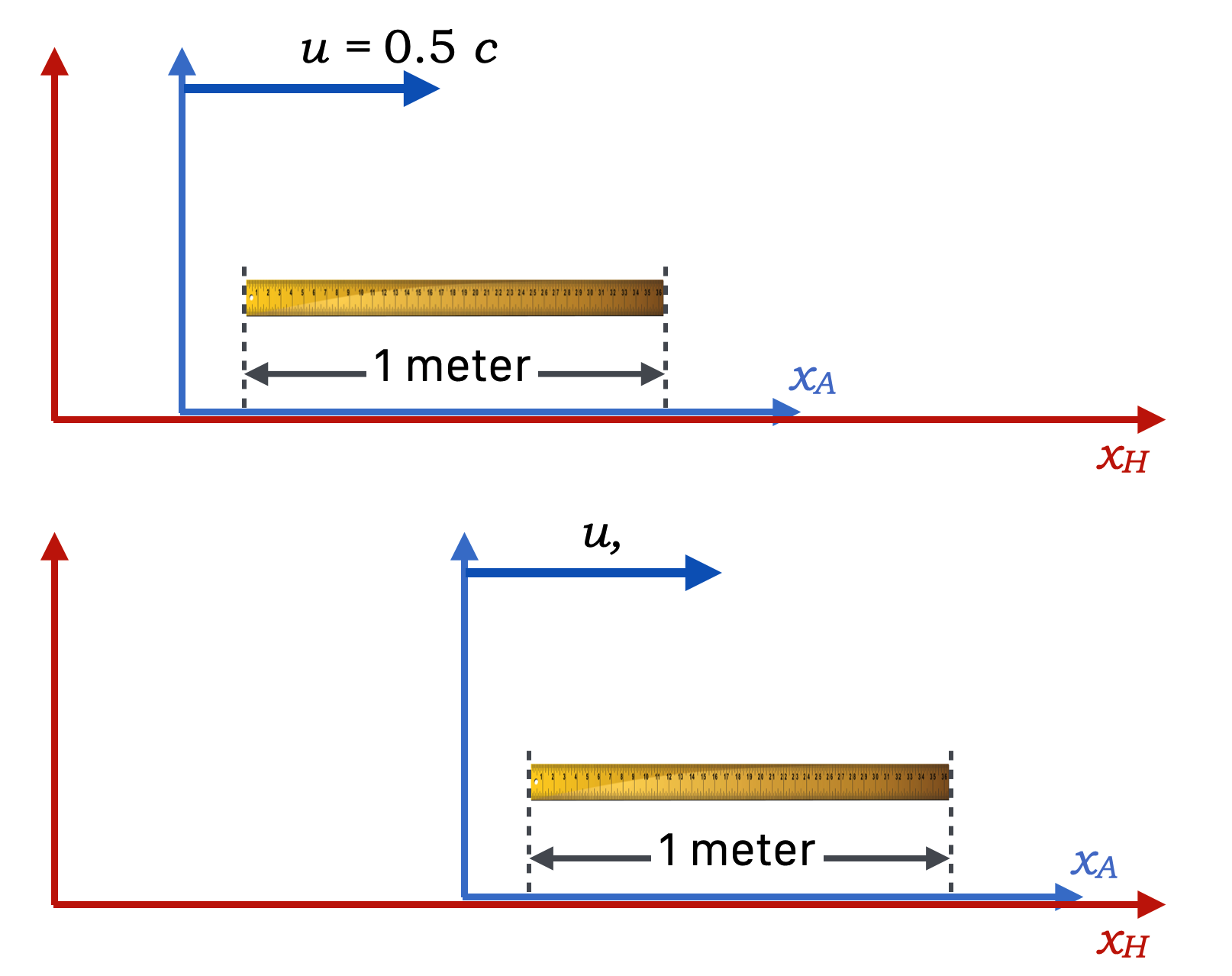
  • Meter stick is own rest frame (the “proper frame”) and of course has a length of one meter. So, \(L_A = 1\) meter.

  • We’re watching it move by us and so our frame is H and the ruler’s frame is Away and is moving at \(u=0.5c\).

How long does the meter stick appear to us in the Home, frame?

galilean_train

The Answer:

The relationship for length contraction is the inverse of that for time dilation. We learned that the \(\gamma\) for \(\beta=0.5\) is \(\gamma = 1.154\) and so we can directly calculate:

\[\begin{split} \begin{align*} L_H &= L_A/\gamma \\ &= \frac{1 \text{ meter}}{1.154} \\ L_H &= 0.87 \text{ meter} \end{align*} \end{split}\]

It appears to us to be shorter by a little more than 10%.

Contents