The Simplest Collision of All, Everyday and Quantum Mechanically

7.6. The Simplest Collision of All, Everyday and Quantum Mechanically#

Now let’s put it to work by solving the simplest collision of all.

Before tackling it, let’s also establish some terminology, some of which is repurposing everyday words into specialized physics terms:

  • I’ll use the words collision and scatter interchangeably.

  • We’ll often call the whole scattering process—objects approaching, colliding, and separating—an event.

  • The state of an object is its particular values of position and momentum. These six quantities are enough to completely characterize an object’s future motion.

  • Let’s treat the moment of collision as a special time in the event serving to separate the initial state [before, our (a)] from the final state [after, our (c)]. So an event consists of the initial state, the collision, and the final state.

  • For our purposes, we’ll reserve the phrase elastic collision to mean that the two objects that scatter at the beginning are the same two objects after they collide. They have different states, but they are still the same objects in an elastic collision.

  • We’ve already met a decay which is an atomic, nuclear, or particle physics idea.

  • And, a reminder about units: remember that the units of momentum are associated with the units of \(p=mv\) , so mass times velocity. So a kilogram-meter-per-second is a perfectly good unit for a momentum. In the English system, so would be slug-ft-per-second, which is a lot of fun to say, but it’s not usually used.

But these units are unfamiliar and could get in the way of grasping the important stuff, so let’s just invent our own unit-less arbitrary measure. If I say that a particular momentum is “5,” we’ll interpret that to be in arbitrary, fake “momentumunits.”

Two more terms which repurpose some regular words:

  • Beam. Any of our objects that are moving toward a collision, we’ll call a beam or beam particle.

  • Target. A beam is aimed at an object which we’ll call it a “target.” Just what is the target and what is the beam is a matter of your point of view, but it will be clear in our contexts. You’ll see.

The simplest collision of all is when the target is sitting still and the beam hits it—like our billiards or ice hockey example. This situation is called a Fixed Target Collision.

Let’s play pool.

7.6.1. The Stop-Shot, Elastic Scattering With a Wrinkle:#

\(\mathbf{A}+\mathbf{B}\to \mathbf{A}+\mathbf{B}\)

Here is the simplest collision of all. It’s a variant of Collision 1 when now the \(B\) ball is sitting still minding its own business and cruelly struck by \(A\). Here it is:

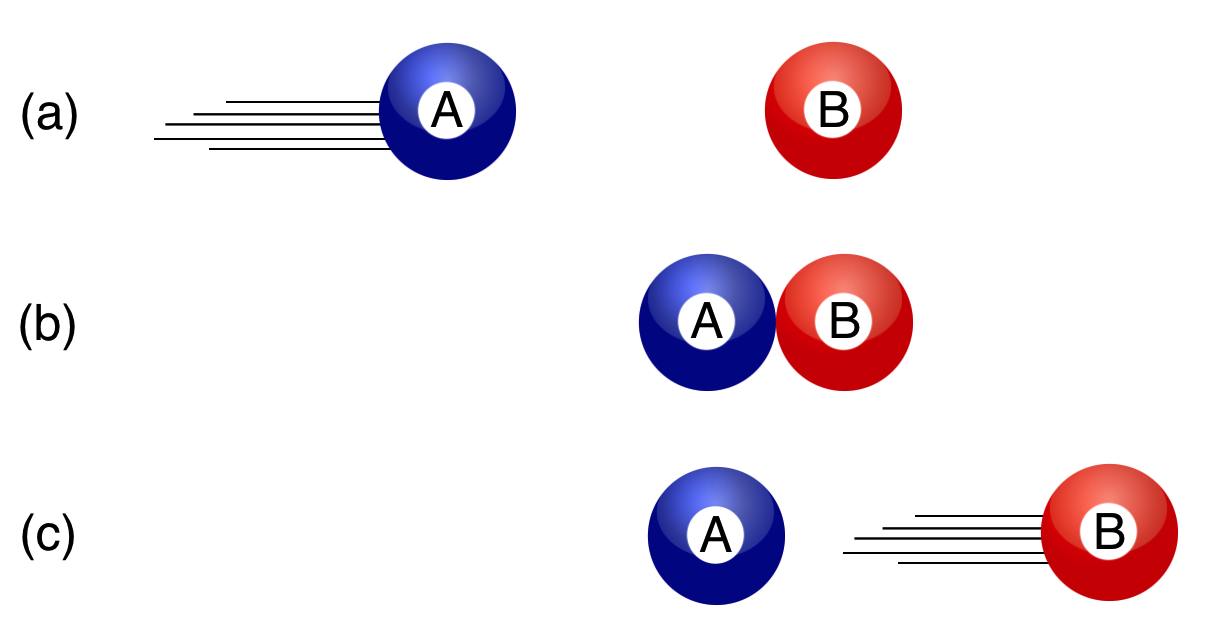
../_images/collide2b.png

Fig. 7.14 TIME GOES FROM TOP TO BOTTOM IN THREE STEPS: An example of Collision 1 in which ball \(B\) is initially sitting still: it’s “at rest.#

You’ve done it with billiard balls: the first one comes in, strikes the stationary one, and it scoots out and the first one stops in its tracks. Can’t get any simpler. It’s called a “stop shot” or “dead ball shot” in pool and so watch it in action in this video clip:

Watch a stop shot video.

Here, Momentum Conservation will be on trial.

This next example walks through a made-up stop shot collision.

Wait. Do I have to? Glad you asked. Well, no. Of course you don’t “have to” but if you just follow the path, you’ll end up knowing a lot more than you do now!. Please do it?

Two balls, each of mass 6 (in made-up units without dimensions attached). Ball \(B\) is sitting still, minding its own business, wehn it’s brutally struck by ball \(A\) which has momentum of 12. A number of questions are asked and answered about this simple collision, so read carefully:

  Please study Example 2:

The stop shot and momentum

If you followed this, then you now have a first-rate appreciation for momentum conservation.

7.6.2. Houston, we have a problem#

We used our experience to determine the final state. But that’s cheating. We should be able to fully predict the outcome. Let’s try that, but first buckle your seatbelt.

  Pens out!

Since our two balls are identical, their masses are the same and we’ll use the single \(m\) for that common mass:

(7.2)#\[ m(A) = m(B) \text{ which we'll call } = m. \nonumber \]

Momentum conservation says:

\[\begin{split} \begin{aligned} p_0(A) + p_0(B) &= p(A) + p(B) \\ mv_0(A) + mv_0(B) &= mv(A) + mv(B) \end{aligned} \end{split}\]

where I’ve put in for the common definition of mass and unique velocity for each ball.

Since \(m\) is the same everywhere, we can cancel them all on the left and right sides. And, for this particular example, \(B\) was sitting still at the beginning…so…what’s its velocity at the end?

Of course, we know that \(B\) is stationary, \(v_0(B)=0\). So, we get:

\[ \begin{align}\begin{aligned} \begin{aligned}\\\begin{split}v_0(A) &= v(A) + v(B). \\ v(B) &= v_0(A) - v(A) \nonumber\end{split}\\\end{aligned} \end{aligned}\end{align} \]

Eq. (7.2) is Descartes’ idea again: the total “motion” of the first object at the beginning is not lost but shared between the motions of all of the objects after the collision.

But we’re not happy. No, not happy at all.

Eq. (7.2) is a simple, but terrible result! The beam object should stop dead. We just saw it with our own eyes. If our model is complete, then it should predict that:

\[v(A)=0\]

and so

\[v(B) = v_0(A) \nonumber \]

but it’s not! It’s \(v(B) = v_0(A) - v(A)\) which includes the correct result, but isn’t uniquely that result.

Wait. You mean that Newton and Huygens were wrong?

Glad you asked. I tried to be careful above in with my, “If our model is complete.” We need more physics! A subject for the next lesson.

Contents