13.4. Electric Field for Other Configurations

The Electric Field for a concentrated charge at a point gives rise to the inverse-squared strength of the above discussion and the radially-outward distribution of the field lines. But what about other distributions of electric charge? Not everything is a point-charge…but all charge distributions can be constructed from point charges. Let’s see. If I bring the proton and the electron closer together we can see that the field lines start to overlap (of course they would overlap to infinity! But here it’s more obvious):

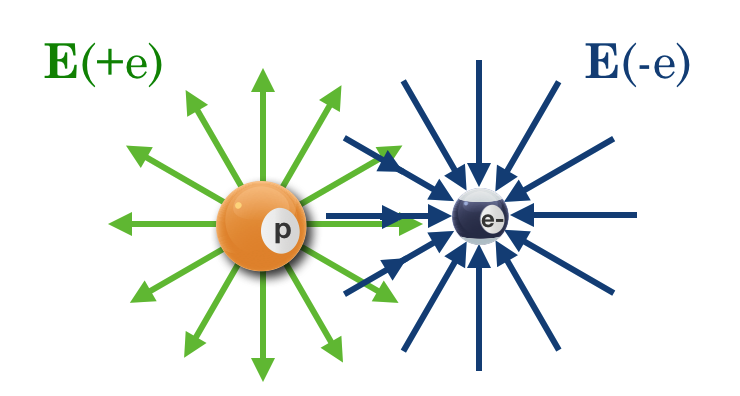
Fig. 13.6 Now there are two charges of opposite sign where obviously it’s apparent that there is a much different force distribution from a single charge and of course, a different field shape. It’s not too hard to think about how this is constructed: just overlay the field of a positive charge (here green) with that of a negative charge (purple) and add the vectors.

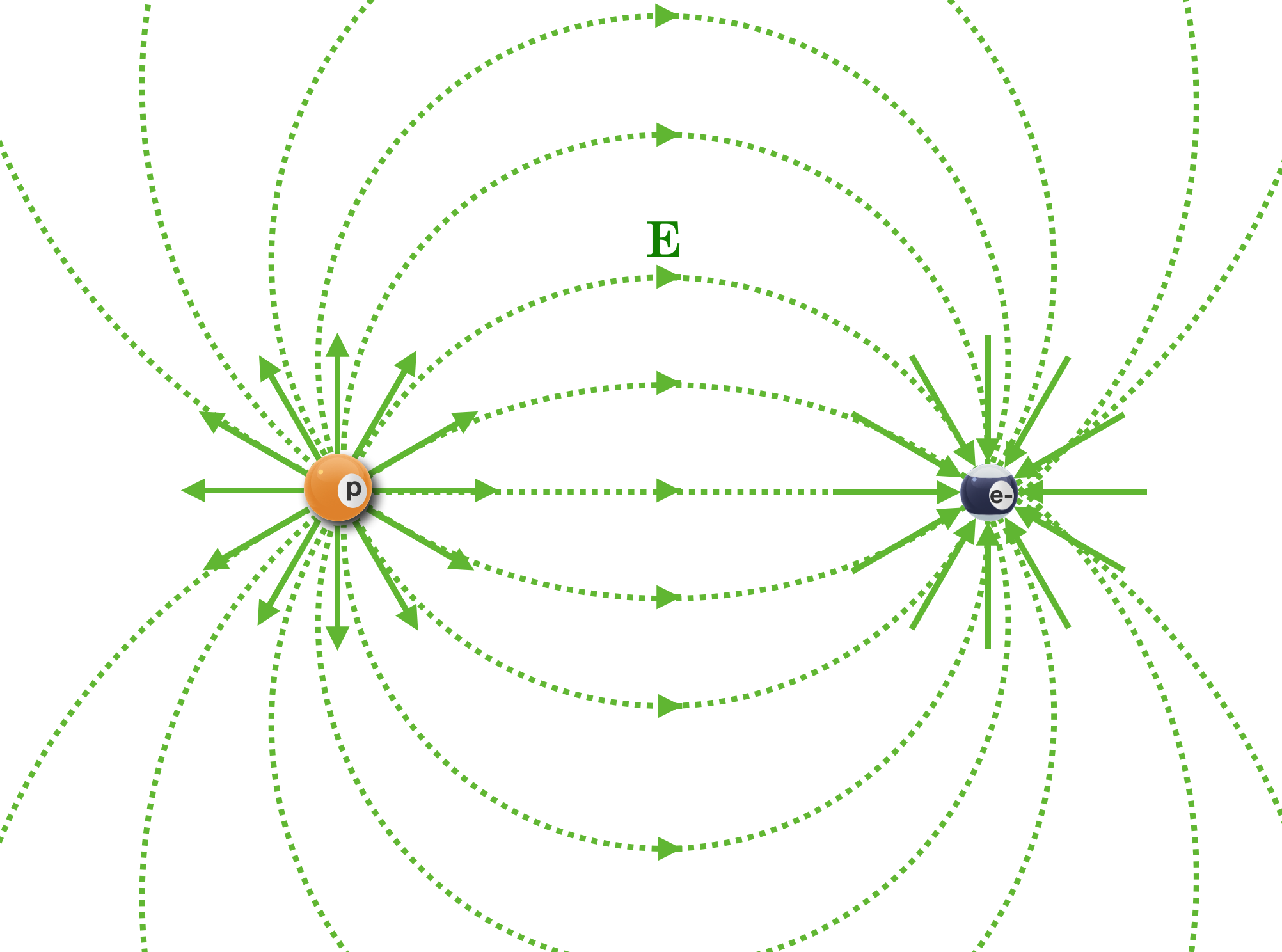
Fig. 13.7 Directly in the middle you can see that they would add constructively and point to the right. Just off the center, they would also add and the results (up or down) would tend to point toward the electron, but less so, since some of the vector addition would cancel in the up and down directions. The side photograph shows the result for two charges of opposite signs. You can see how the field lines connect as they twist the little pieces of dielectric to align. The sketch below shows this in an abstract way.

13.4.1. Line of Charge

  Pens out 🖊

Let’s look at charges of the same sign, lined up side by side. This figure shows two positive charged and in the middle a region where I’ve extended two of the field lines over one another as the dotted vectors.

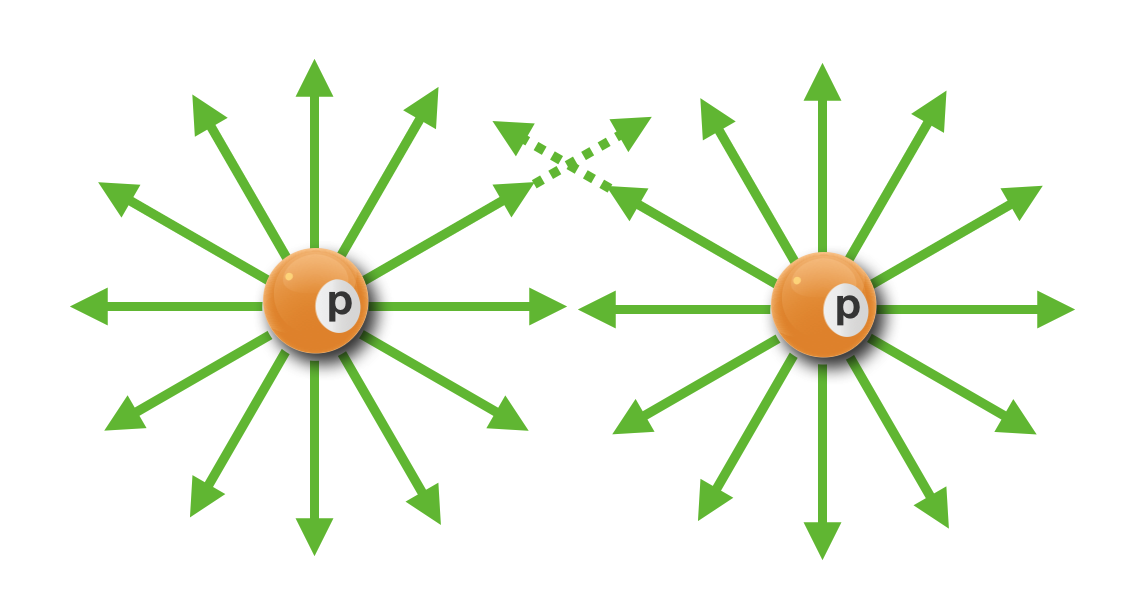
Can you see that in that the horizontal components of the dotted vectors will cancel, right minus left, whereas the two vertical components would add and point up? Every single field line pair of the two charges will do exactly that, leaving the net field: up or down (above or below the line connecting the charge-centers).

Fig. 13.8 We can also see that in the photograph. Notice that there’s essentially a void between them where the field lines essentially cancel near the center-line.

Now we have the building-blocks of a number of different electric field arrangements. Let’s toe the line.

Suppose we now align an infinite number of identical charges, side by side on a straight line extending to infinity in each direction. What would the electric field look like for that combination? I think you can “see” it in your mind’s eye. All of the adjacent field vectors would cancel any horizontal components, neighbor by neighbor. Meanwhile, all of the vertical components would add. The end result is an electric field configuration that would point radially outward from the line — which we can imagine now as a wire with excess charge. This figure shows the result in three different views.

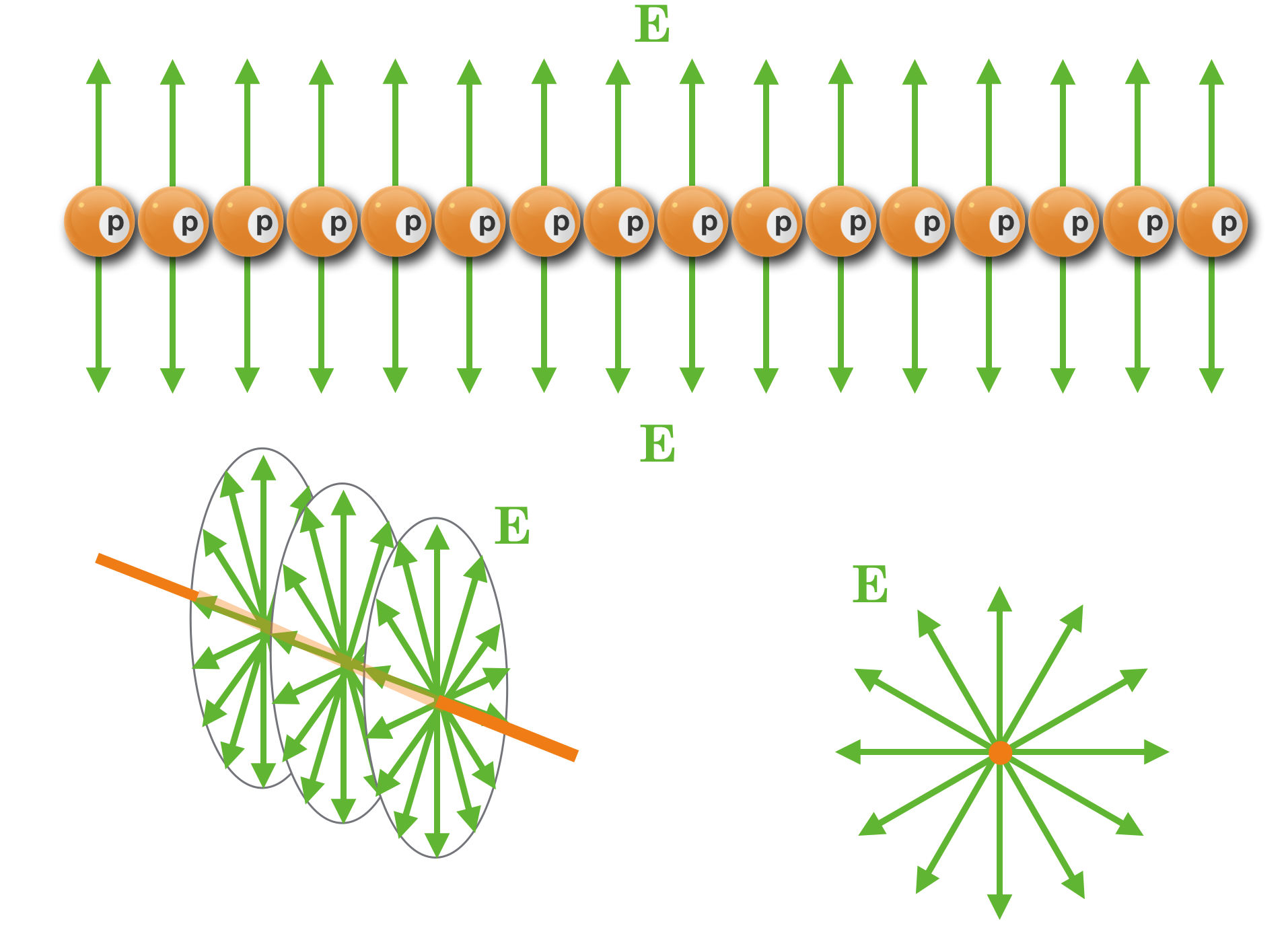
Fig. 13.9 It’s not very hard to extrapolate to a sheet of charges from this single line of charge. You just have to imagine laying an infinite number of lines of charge, side by side. The result: a three dimensional electric field, uniformly perpendicular to the “sheet” and pointing above it and below it. Here’s a segment of such a sheet:

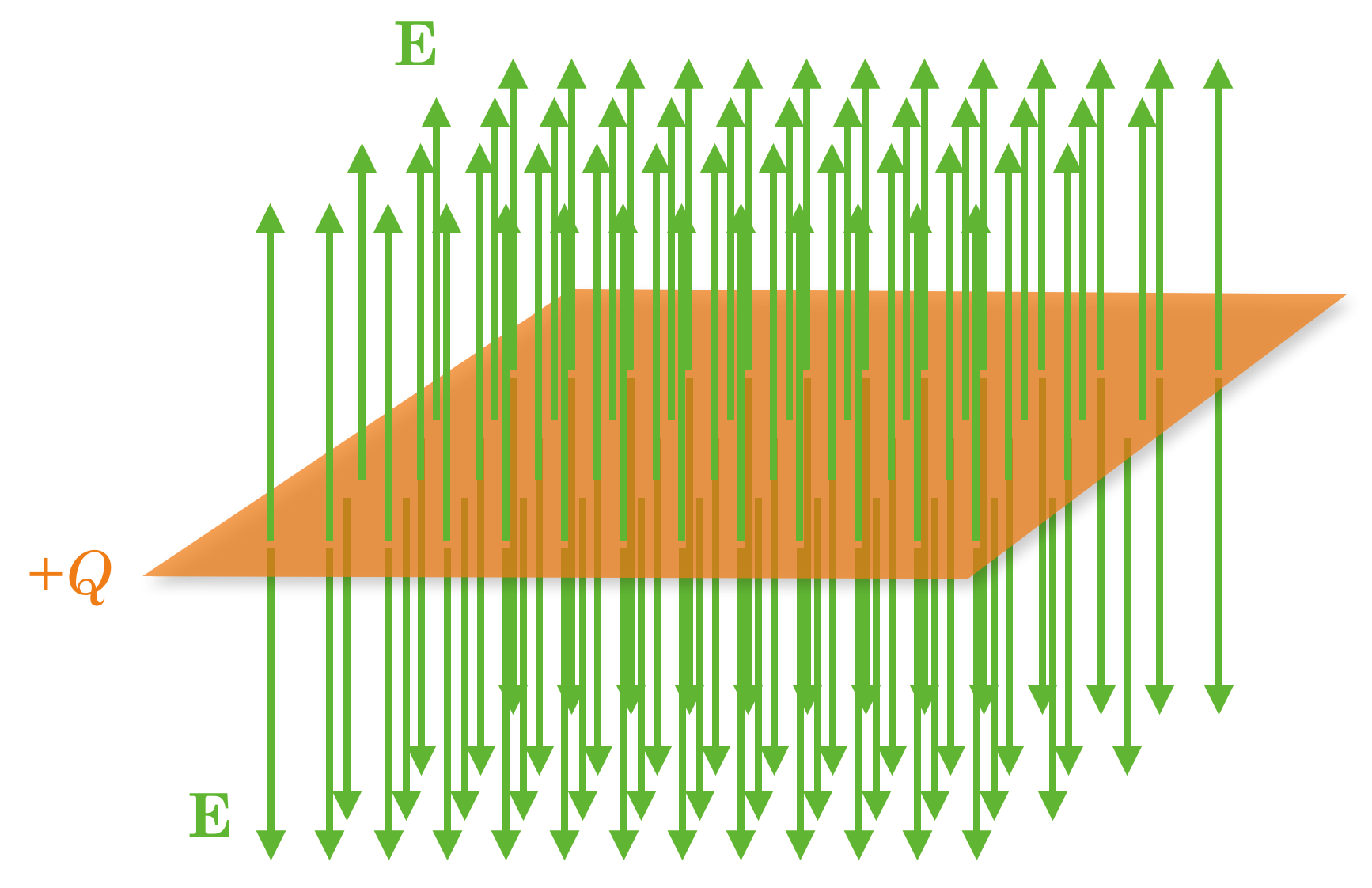
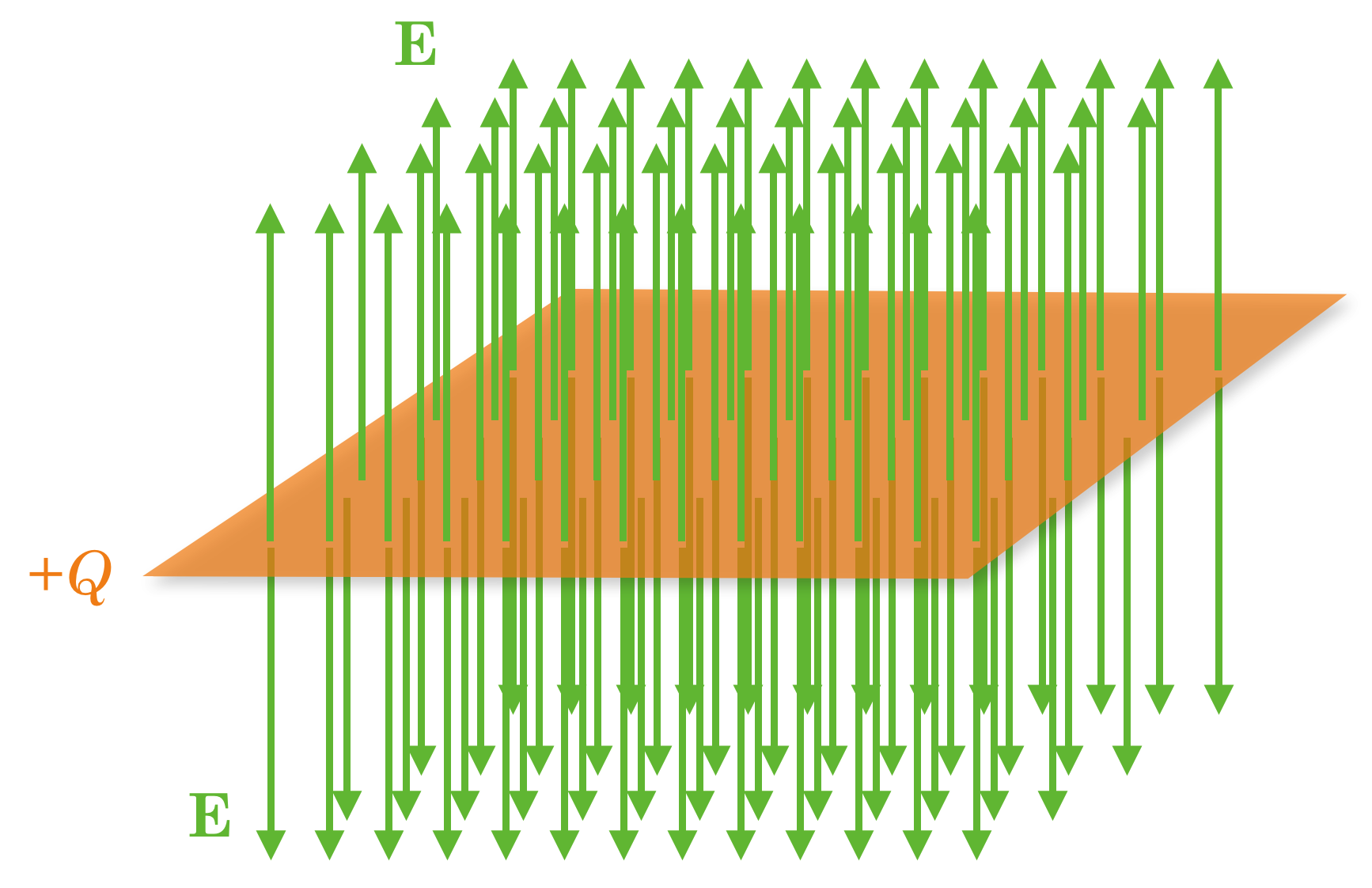
Fig. 13.10 Suppose we made our sheet not from positive charges, but from negative charges. Then the arrows would all point towards the sheet rather than away from it. Here’s how that would look:

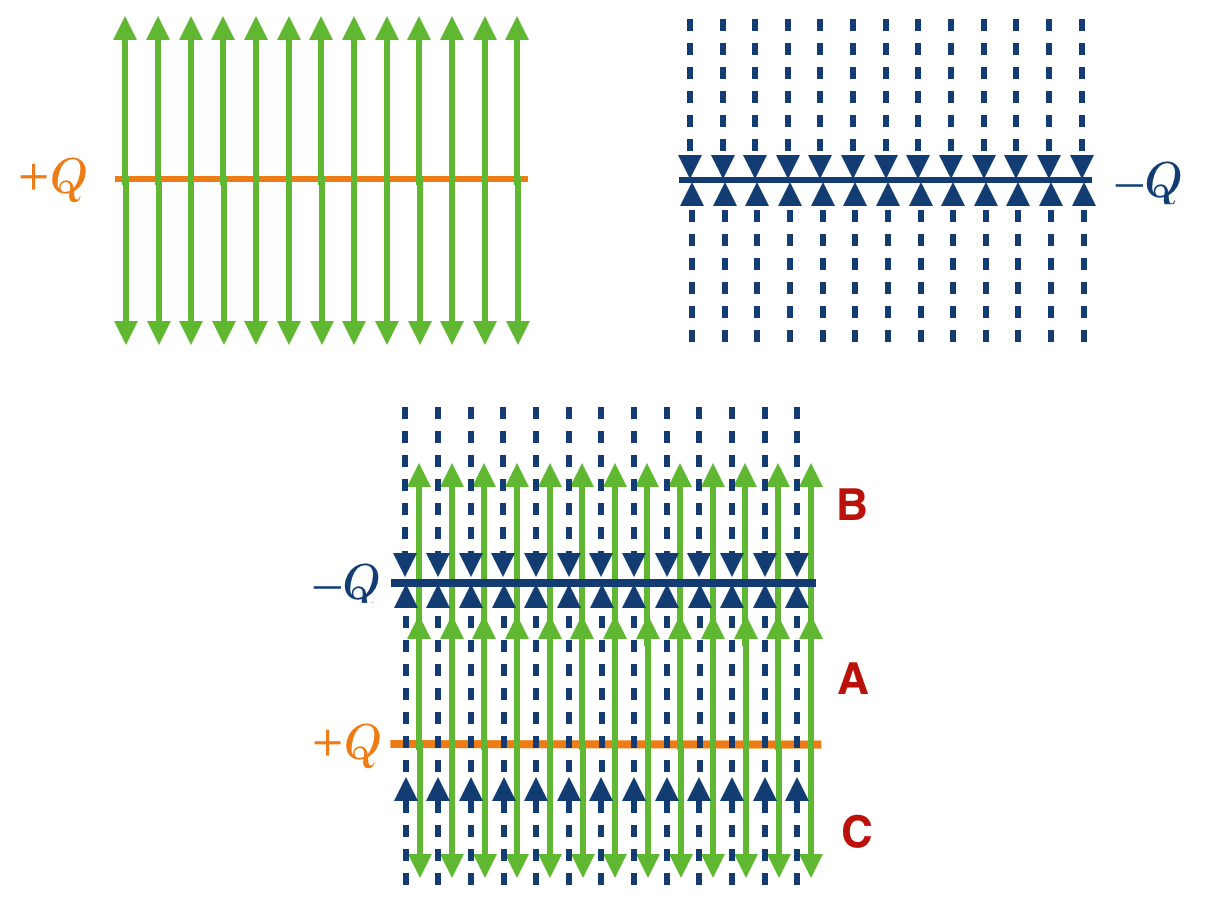
Fig. 13.11 Now let’s make a sandwich of two such sheets which have been prepared with the same magnitude of charge, but with one positive and one negative. The “meat” part of the sandwich we’ll take to be empty space. If the negative sheet is on top and the positive sheet on the bottom then the vectors from the bottom point up (the orange solid vectors) between the sheets while the vectors from the top (negative) plate point up toward from it. Now we can look in three regions:

A. and C. The regions outside of the middle have the orange solid \(\vec{E}\) vectors from the positive plate pointing in the opposite directions from the blue dashed \(\vec{E}\) vectors from the negative plate: they cancel.

B. The meat part of the sandwich between the plates shows that the \(\vec{E}\) fields are aligned in that region.

Don’t take my word for it. The next photograph shows the field lines between two parallel plates in the same dielectric material that we showed point electric charges and the dipole.

Fig. 13.12 What could cause this arrangement of charges, and hence this configuration of \(\vec{E}\) fields? This cartoon sets up that narrative. A simple battery does the trick:

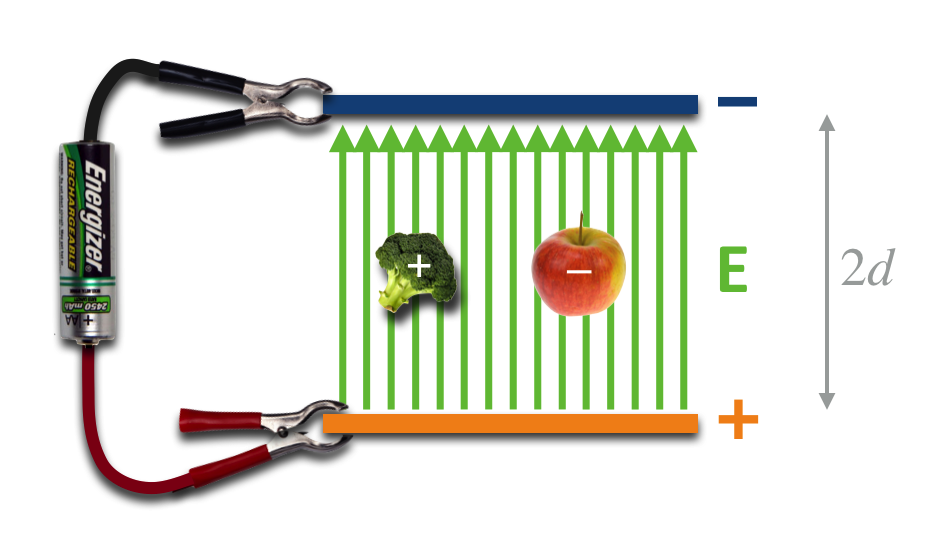
Fig. 13.13 This combination of metal, wires, and a battery creates a beautifully uniform and functional designer-electric field. It’s confined to the region only between the plates (if the are large in area as compared with the spacing between them) and the field created is uniform throughout that volume. In circuits such a device is called a “capacitor” but in our QS&BB life, it’s a particle accelerator.