15.7. More Trouble With Light#
Einstein often asked deceptively simple questions. Here’s one from when he was 16 years old. Remember that electromagnetic waves propagate because the electric and magnetic field vectors mutually nudge one another:
A changing electric field creates a changing magnetic field and
A changing magnetic field creates a changing electric field.
And so it goes: the result is an electromagnetic wave in which the two are coupled together and self-generate their propagation.
Teenage Einstein wondered what would happen if an observer were to speed up alongside of a light beam so that she was traveling at the same speed as the light? The “changing” pattern of the two field vectors would stop if you’re right alongside. And, if they aren’t changing in time, then there’s no mutual influence of one on the other and there’s no wave.
Not only that, time would appear to stop. For example if you were watching the hands on a clock as you sped away, the reflected light from the clock hands would struggle to keep up with you if you’re traveling at near-light speeds. When you reach \(c\), all you would see would be the clock hands frozen at the last moment before the reflected light could no longer reach you.
That was a problem for which he had no solution. And it nagged him into adulthood.
15.7.1. EM Weird #1#
Remember my fascination with the current loop and a magnet? This is why.
Note
Watch closely: this is a strange situation.
Let’s define our two different scenarios:
In the first part of the video, the coil is stationary with respect to the desk and the magnet is in motion. Call this scene: “Coil Stationary,” CS.
In the second part of the video, the magnet is stationary with respect to the desk and the coil moves. Call this scene: “Magnet Stationary,” MS.
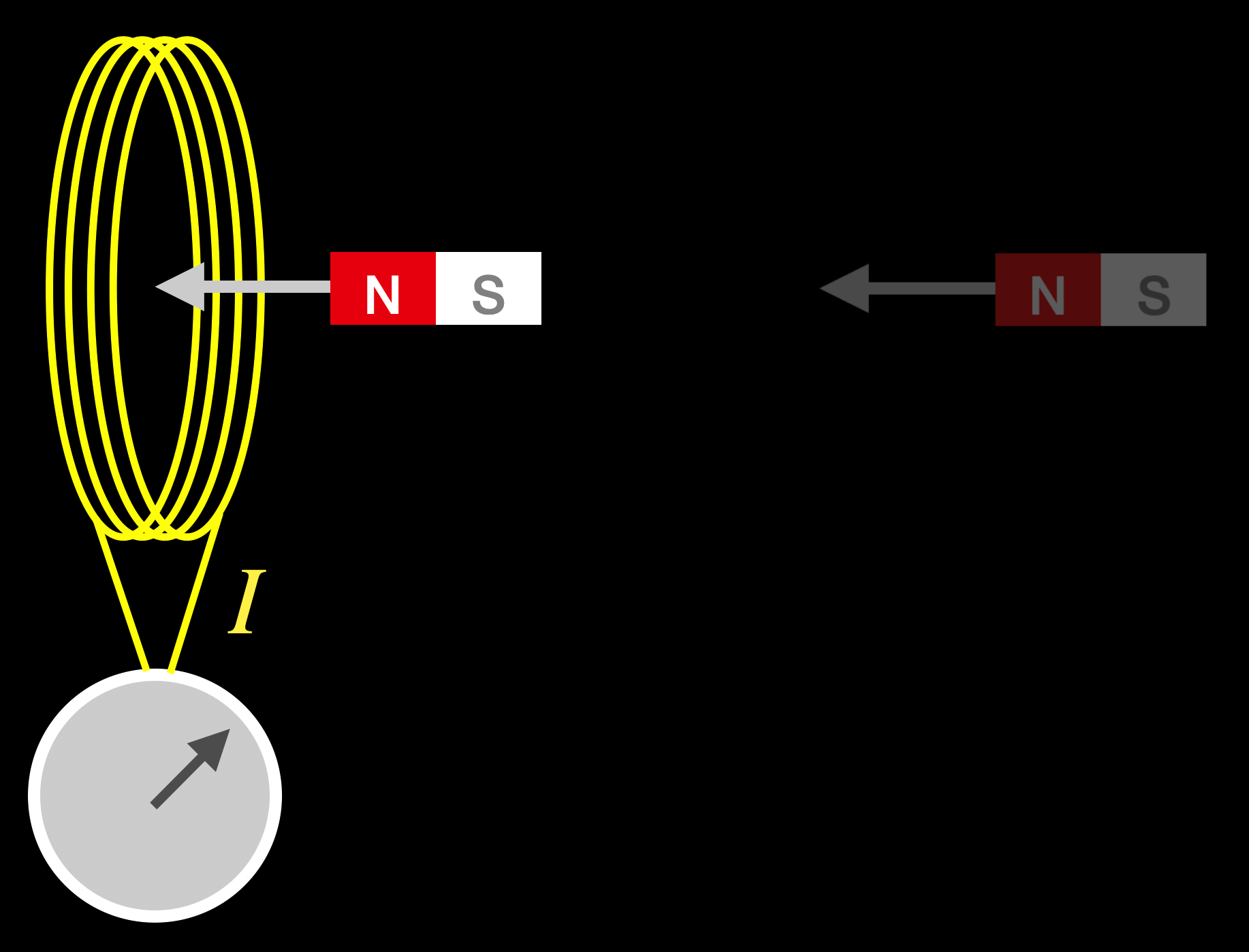
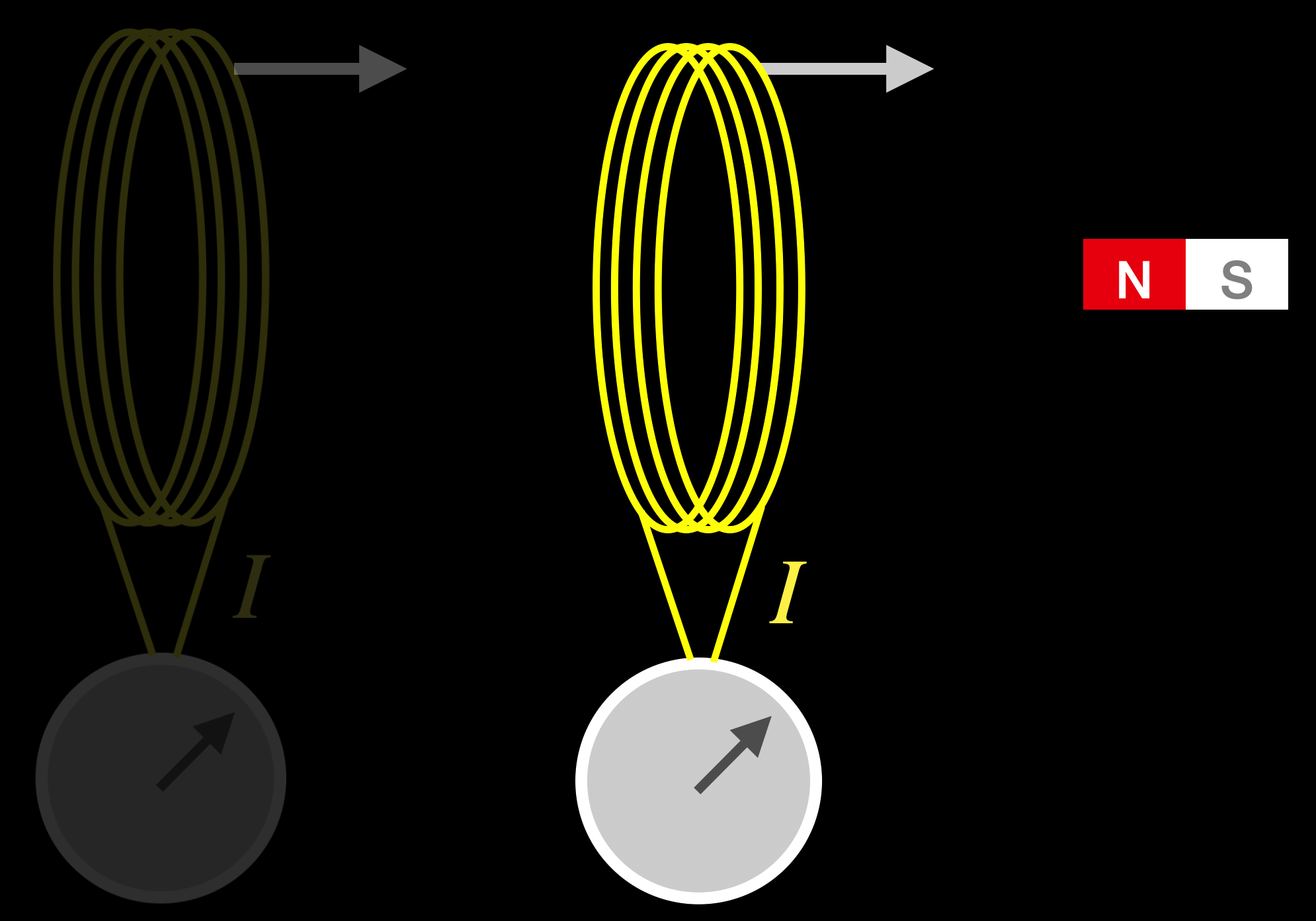
The result is identical: Both CS and MS cause a current and the galvanometer shows that.
What’s the problem?
Glad you asked: The problem is that the reason that a current flows in CS is due to an entirely different physical process than for MS.
We get the same result for two circumstances that only differ by the relative motion of the two pieces. But, the physics reasons are entirely different!
CS. Like Maxwell said and his equations would require, in CS the moving B field creates an E field in the vicinity of the wire in the coil. That E field in turn applies a force on the electrons in the wire and a current flows.
MS. Like Maxwell said, and his equations would require that in MS at my desk there is no E field produced because the B field does not change in time. But, the electrons in the wire are moving with the coil as it’s shoved toward the magnet and so they have a velocity relative to that B field. Lorentz’s force then causes the electrons to feel a force perpendicular to their velocity–and so they move! Inside of their wire in the coil, which is a current!

Here’s another one.
15.7.2. EM Weird #2#
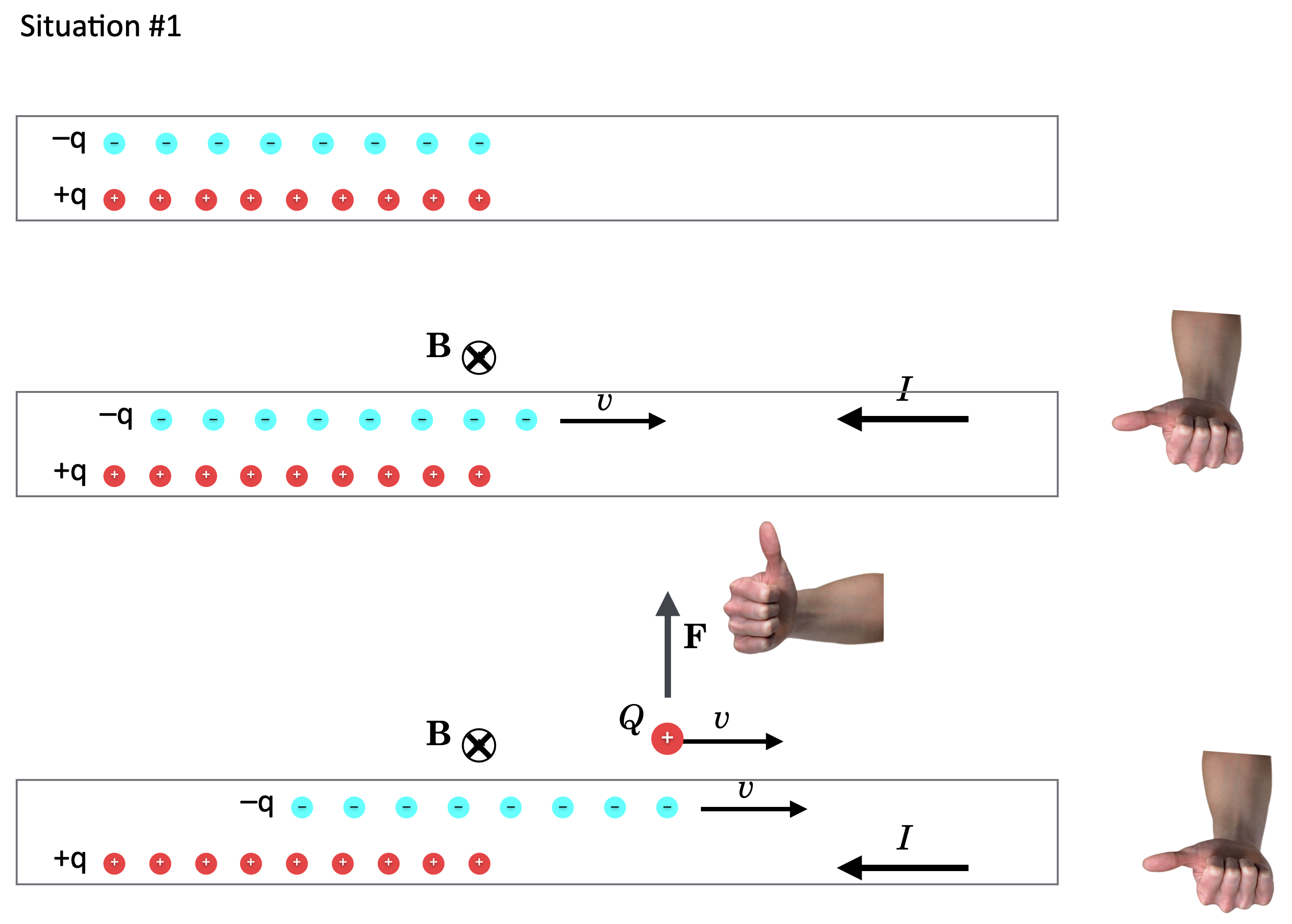
Scenario #1, which I’ll call “Q moving,” QM. Imagine that we have two lines of charge, one positive and one negative and each with the same number of \(+q\) and \(-q\) elements as shown in the top of the figure. Now we cause the negative line of charge to move to the right as in the middle figure so sitting outside of them, it would appear that there is a current \(I\) flowing towards the left (remember thanks to Ben, we mark current’s direction opposite to electron flow). That current would then create a magnetic field, B, in a circular shape around the line of \(-q\) charges. Using your right hand, you can see that it would come out of the screen at the bottom and to into the screen at the top, right? This is in the middle figure.
Now let’s place a new, isolated positive charge \(+Q\) above the line of \(-q\)’s as shown in the bottom of the figure and cause it to have the same velocity to the right and ride along with the line of \(-q\) charges. So \(+Q\) and the negative \(-q\)’s are relatively stationary. It sees no current due to the negative line of charge, since it appears to not be moving relative to it. But it does see that same current, \(I\) now due to the relatively moving positive line of charge that appears to \(Q\) to be flowing to the left. \(Q\) now feels that B field — in at the top and out at the bottom — and so by Lorentz’s force relationship, it feels a force pointing up and so it would curve up.
Scenario #2, which I’ll call “Q stationary,” QS. Now let’s mix it up by creating the same current in a different way. Let’s keep the \(+Q\) charge and the line of \(-q\) charges stationary (like in the top of this figure) and cause the \(+q\) line of charges to move to the left as in the middle of the figure. That also creates an identical current to the left, \(I\). So that current part of QS is the same as in QM. That moving positive line of charge’s current also creates a magnetic field with the same configuration as in QM. But! \(+Q\) is just sitting there — it has no velocity in this scenario — so it does not feel a force from B and doesn’t see a force and stays unmoved!
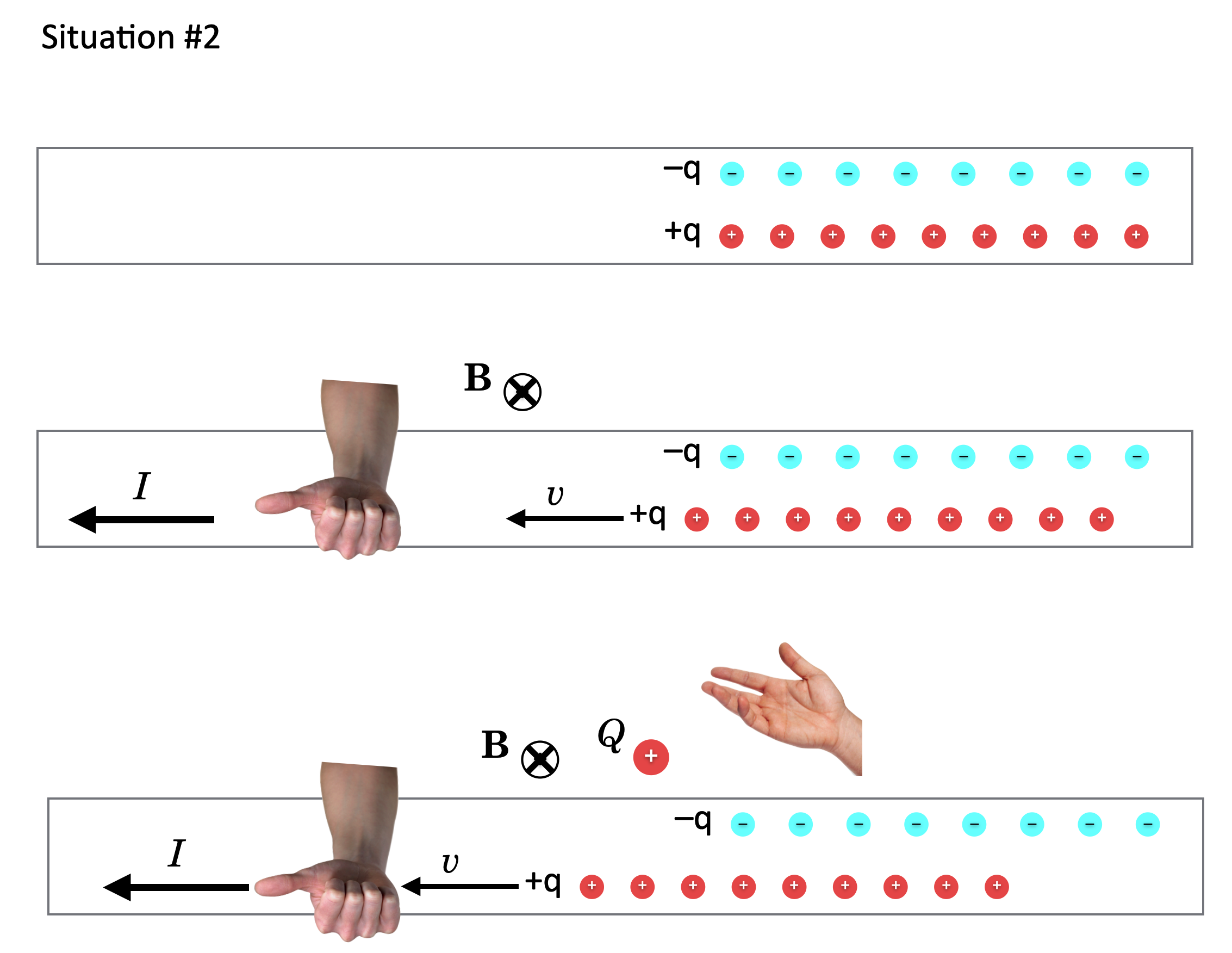
QM and QS appear to be identical situations overall: both have a current flowing to the left and identical magnetic fields. Both have a positive charge \(+Q\) which is in the same relationship to the \(-q\) line of charge: at rest with respect to it. In QM, they both move while in QS, neither moves.
But: the physical outcome is different! In QM, \(+Q\) feels a force and would move up and in QS, the \(+Q\) would not feel a force and just stay still.

In both of these examples Maxwell’s Equations seem to fail for scenarios that differ only in the relative speeds of the observer.
So something must be wrong with Maxwell’s equations? How about Newton’s laws of motion?
15.7.3. Newton Seems Fine#
Pencils Out! 🖋 📓
Suppose you’re in an airplane traveling at 500 km/h to the east and you’re bored so you start to roll apples along the aisle. It’s a long flight and you’ve got plenty of time to practice and you learn that you can start rolling your apple at 5 km/h and that after 2 seconds it will have slowed to 1 km/h. If your apple is like our QS&BB apples it has a mass of 0.1 kg, we can calculate the force that’s applied to the apple by the floor to slow it down:
(Of course the negative sign tells us that the force is pointing away from the direction of the velocities and so it’s decelerating.)
I’m on the ground and I’m also bored and I have a very fine telescope that allows me to watch airplanes as they fly overhead. It’s a comic-book telescope and so I can see through the hull and into the airplane and I can watch you roll your apple. What would I say is the force that the carpet is exerting on your apple to slow it down?
Just as you’d expect: Newton’s laws of motion work just fine between two systems that differ only by their relative speeds. Remember this moment.
Note
Two great theories – of electricity and magnetism and mechanics – behave very differently when applied to circumstances that differ only by the state of motion of the observer. Circa 1900, here’s the what people were convinced of:
Count on it: 1. Newton’s laws of motion are well behaved.
Count on it: 2. Maxwell’s equations of electromagnetism fail outside of the ether.
That’s a disaster and it bothered Albert Einstein during a particularly important year in his life which we’ll talk about a lot in the next lesson.
But let’s go to the airport and think about moving sidewalks.
15.7.4. Frames Of Reference#
I’ve not been able to make fun of Aristotle for a number of lessons and I miss that. So let’s let Galileo speak for himself and put another nail in the coffin that was once Aristotle’s physics.
15.7.5. Galilean Relativity#
Suppose we are on a ship with a tall mast and a sailor in the crow’s nest with, of course, an apple. Let’s consider two scenarios:
Scenario #1, which I’ll call “In port,” IP. In this situation, our sailor in the crow’s nest drops his apple.
Scenario #2, which I’ll call “Under sail,” US. In this situation the ship is moving west and our sailor again drops his apple.
Mr Aristotle would have said that in IP, the apple would fall to the base of the mast, directly from \(A\) to \(B\). Galileo would agree.
Pencils Out! 🖋 📓
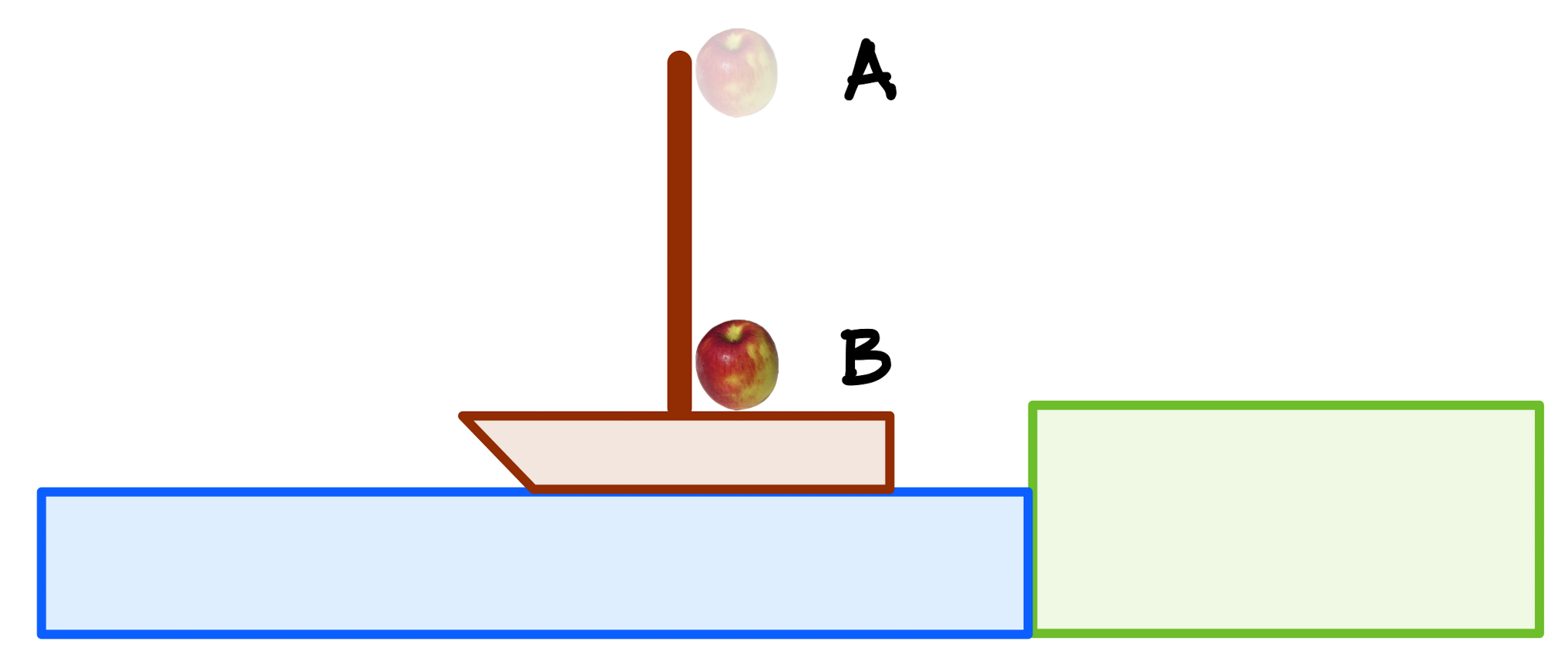
But Aristotle would say that in US, the apple would fall to the east of the ship, to \(C\) since the ship has sailed right out from under it. Here you see the ship moving to the left (west) and the apple making a strange journey from \(A\) to \(C\):
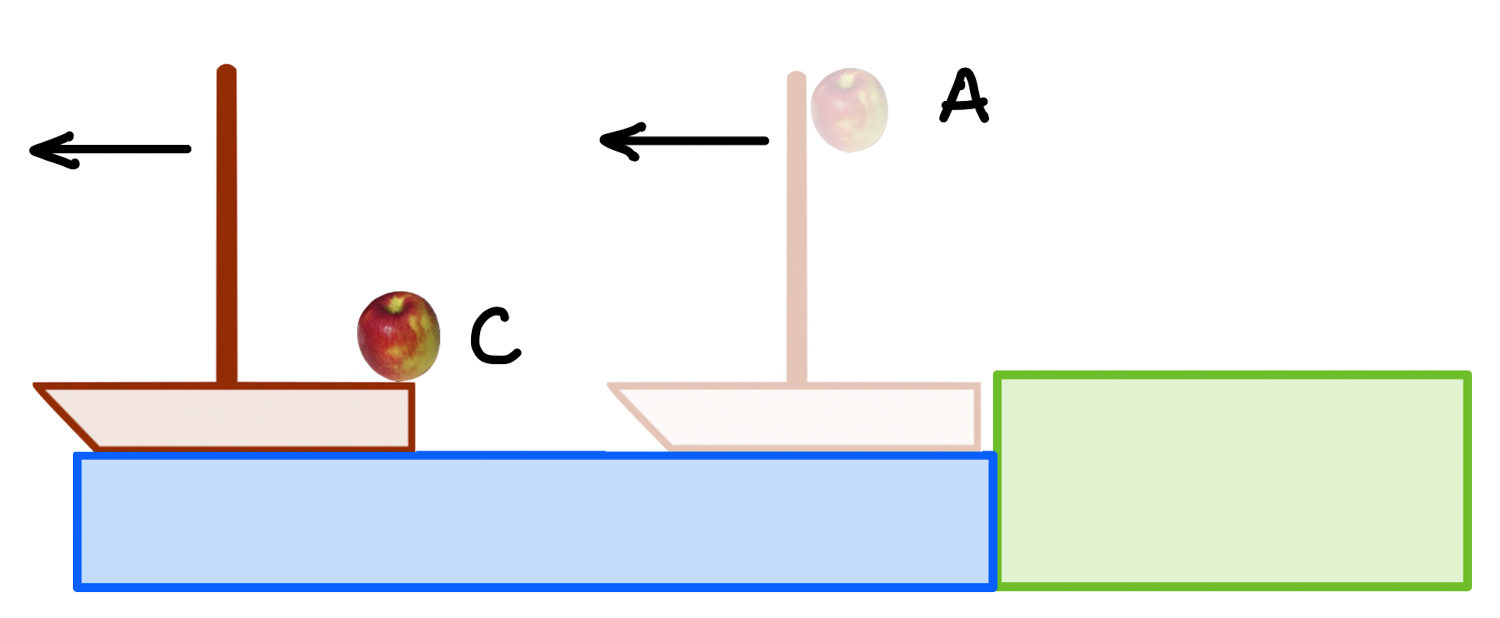
Does this make any sense to you? (Think about your apple-roll on the airplane.) Of course not and like so many other times, Locomotion for Aristotle fits his complicated philosophical system, but fails to match even the simplest glimpse of reality.
“Observation versus Authority: To modern educated people, it seems obvious that matters of fact are to be ascertained by observation, not by consulting ancient authorities…Aristotle maintained that women have fewer teeth than men; although he was twice married, it never occurred to him to verify this statement by examining his wives’ mouths.” Bertrand Russell, The Impact of Science on Society, p. 7. Simon & Schuster Inc, 1968
Now, while Aristotle might have been a pretty good observer, except perhaps in matters of dentistry, he surely never dropped something from within a moving airplane, or for that matter a ship. If you’ve ever flown on a plane or ridden in a car or a train, you’ve probably dropped something. It doesn’t land behind you.
But can you see that this example kind of rhymes with the examples from electromagnetism that we just went through? Something odd happens between two systems, one at rest and the other in motion.
Here’s another example, more reasonable. And a bit newer, only 400 years ago. From Galileo’s Dialogue:
“Shut yourself up with some friend in the main cabin below decks on some large ship, and have with you there some flies, butterflies, and other small flying animals. Have a large bowl of water with some fish in it; hang up a bottle that empties drop by drop into a wide vessel beneath it. With the ship standing still, observe carefully how the little animals fly with equal speed to all sides of the cabin. The fish swim indifferently in all directions; the drops fall into the vessel beneath; and, in throwing something to your friend, you need throw it no more strongly in one direction than another, the distances being equal; jumping with your feet together, you pass equal spaces in every direction…have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still.”
This is among the most important observations in physics. What he’s saying is that US should result in this apple’s trajectory:
Pencils Out! 🖋 📓
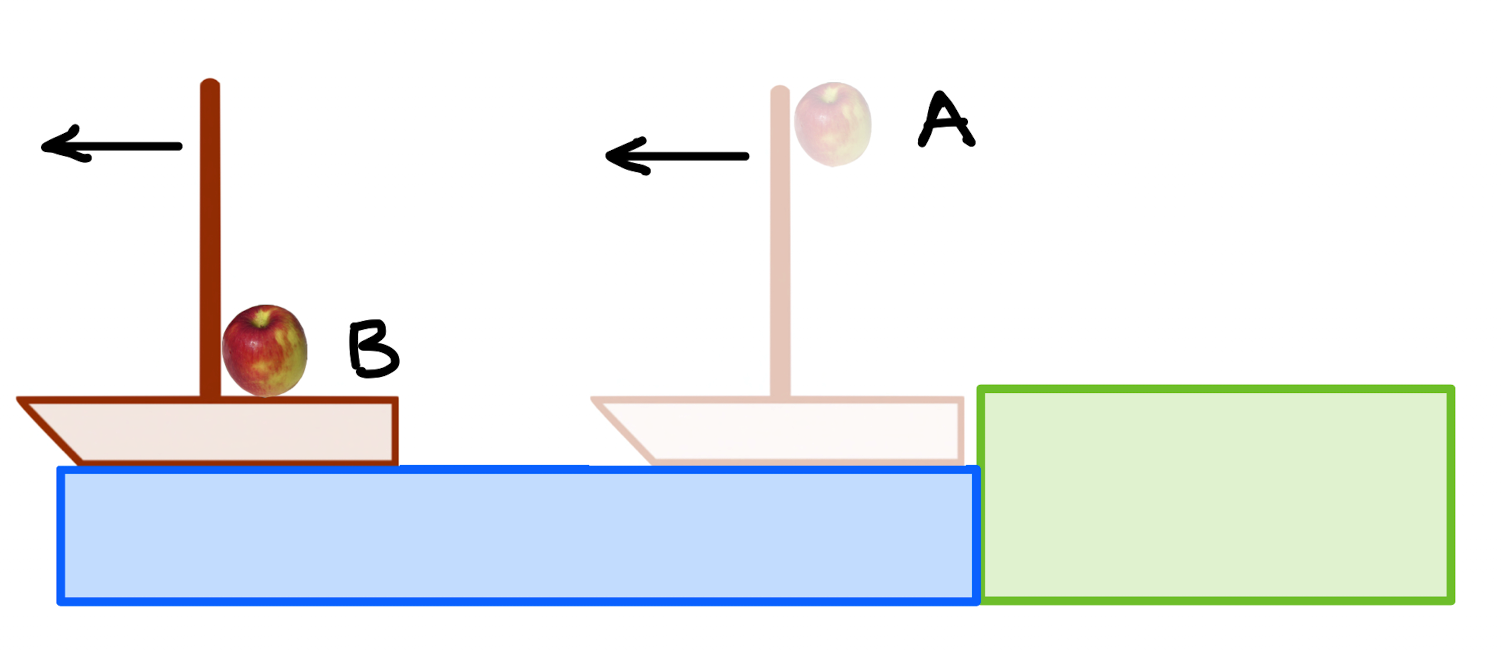
We call this idea Galilean Relativity and it says that:
Galilean Relativity
There is no mechanical experiment that one can perform that can measure whether one is moving at a constant velocity or standing still.
These two circumstances, moving at a constant speed and standing still, seem like very differently things. Stay tuned.