5.13. Projectiles

Throwing things was hard to understand.

Projectiles, Aristotle’s way

Where Aristotle got himself into big trouble was with projectiles, like a thrown spear. His philosophical system came before explanation so he had to do an embarrassing dance to explain that when a rock was thrown the continuous “push” that he insisted was needed came from the displaced air rushing around behind the rock and pushing it forwards. Seriously. Everyone knew that this was nonsense. How can you throw a pointed spear sharp end first and then blunt end first? His authority was absolute, and organization of the first medieval universities with Philosophers and Theologians at the top guaranteed that natural science was taught by them. Mathematicians and astronomers had supporting roles that were aimed at more mundane activities like casting horoscopes and designing military weaponry and fortifications.

Although we’ve been dealing with 1-dimensional motion, Galileo wasn’t done when he figured out that everything falls at the same, constant acceleration of gravity. He also tackled the other problem that Aristotle messed up: throwing something. With an understanding that objects would happily move at a constant speed without being pushed (his two inclined planes) and that objects fall towards Earth with a common acceleration, he had the genius idea to embed these two different motions together into the motion of a single, thrown object. Let’s follow his experiment by looking at his notes in the figure below.

This was first considered by him when he was on his way to Padua from Pisa. He stopped in Urbino along the way to visit his friend and supporter, Guidobaldo del Monte. Remember, it was he who recommended the 26 year old Galileo to his brother, the Cardinal which induced his Pisan position. Del Monte was a mathematician and natural scientist and together they played with rolling balls across an incline. Imagine taking a plank of plywood and propping it up a few inches on one side along the ground. Now take a ball and cover it with paint and roll it up the incline at an angle. It would leave a mark from the paint and trace out…a parabola as it goes up and comes back down. Just who’s idea that was…is one of those things left to the darkness of history. But parabolas were on Galileo’s mind when he took it further and more seriously later.

What you see are various measurements of rolling a ball off the surface of a table and marking where it lands according to how fast it was going. How did he repeat measurements so that each attempt would be the same speed upon lift-off? He rolled them from an inclined plane where he could dial-up the speed he wanted by how far up the plane he let go of the ball as shown in this figure, again from Galileo’s notes:

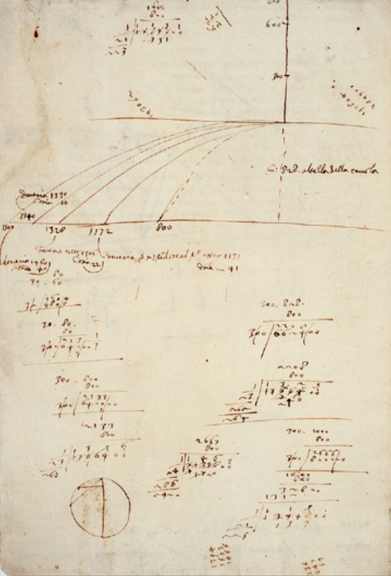
Fig. 5.30 Galileo’s notebook in which he studied the shape of the trajectory of a projectile starting with a horizontal velocity.

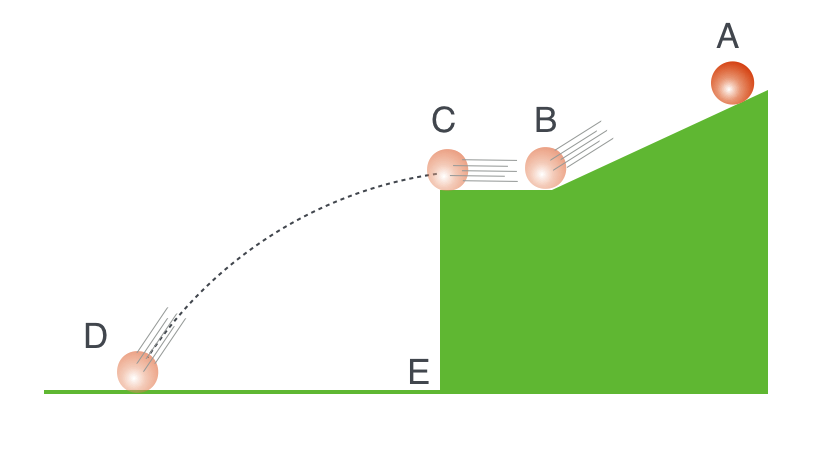
Fig. 5.31 A cartoon showing Galileo’s method. He released a ball at the same height on an inclined plane every time, thereby insuring that when it reached the bottom at B it would have the same velocity for every trial. The velocity at C is then controlled and the point of impact, D, was tallied for many trials.

Clever, no? So let’s think like he did. If the speed of the ball at B is \(v_x\), then what’s the speed of the ball just at the edge of the table, C? It would be the same, which we’ll call \(v_x\). Now when the ball flies off into space it acquires two separate motions that are combined: the ball continues to have the unchanged horizontal speed, \(v_x\). But as it falls, it starts to acquire a new vertical motion, because it’s now accelerated down at a rate of \(g\). The two motions are separate, but together! So throughout the trajectory, the ball’s horizontal speed remains \(v_x\). Nothing has happened to change that. The ball’s vertical speed increases as the ball “falls” along this curved path.

Now here’s the neat thing. Suppose at the same point where the ball leaves the table, another ball is allowed to just drop from that point, say at point C in the figure above so that it falls (only under the influence of gravity!) to point E. This one has only one kind of motion, vertical and accelerated. But it’s accelerated by the same amount as the first one and from the same vertical height, at the same time. So which one reaches the floor first? They both reach the floor at the same time.

This bundling up of two separate motions into one object was inspired reasoning. Nobody had ever conceived of that sort of thing. By analyzing the landing point and some sophisticated solid geometry, he was able to extrapolate to perfect conditions and assert that the trajectory that the ball – any projectile, a cannonball, a spear, an arrow – followed was that of a parabola.