16.3. What Was the Cause of That Storm? The Second Postulate’s Implications

The Second Postulate plays havoc with my common sense, and I’ll bet yours also.

Einstein, more than anyone before him, set up experiments…but not in a laboratory. In his brain. He called them Thought Experiments…Gedankenexperiments. They’re stories that stress the logic of a model if not the mathematics. While they might be hard to actually perform in reality, they stress-test a model for consistency and force conclusions that are sometimes (usually, from him) surprising. If you buy the model, then you’re obligated logically to buy the conclusions. So here’s our first one: baseball.

Let’s look at the crafty Chicago Cubs pitcher, Kyle Hendricks. (Called The Professor due to his mathematically intense Economics degree from Dartmouth College.) Hendricks is not going to terrify any hitters with the velocity of his pitches, but he’s not going to throw the ball into the strike zone either.

He’s known for his unusual training regime. For example training, on the train.

Note

Here we see him pitching to Willson Contreras. On flatcars behind Wrigley Field. The ball leaves his hand at 80 mph. The Professor has some questions:
What is the speed of the ball that Contreras experiences?

  Okay. Isn’t it just 80 mph?

  Glad you asked: Good. Of course.

Note

Now the pitcher’s car is moving towards the catcher at 50 mph and he throws his standard, consistent pitch at 80 mph relative to his car. What is the speed of the ball now that Contreras experiences?

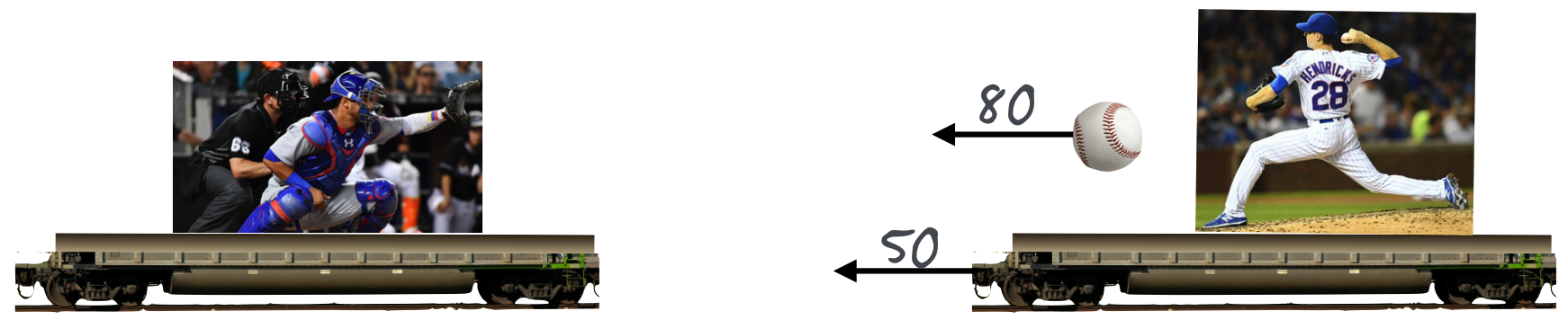
  Okay. Well, now the ball has both the speed of the pitchers throw plus the speed of the car that he’s riding on. The catcher is still staionary, so he sees \(80+50=130\) mph.

  Glad you asked: Yup. Makes sense, right?

Note

Now. The catcher’s car is moving toward the pitcher’s car which is still moving at 50 mph. What’s the speed of the ball that the catcher feels?

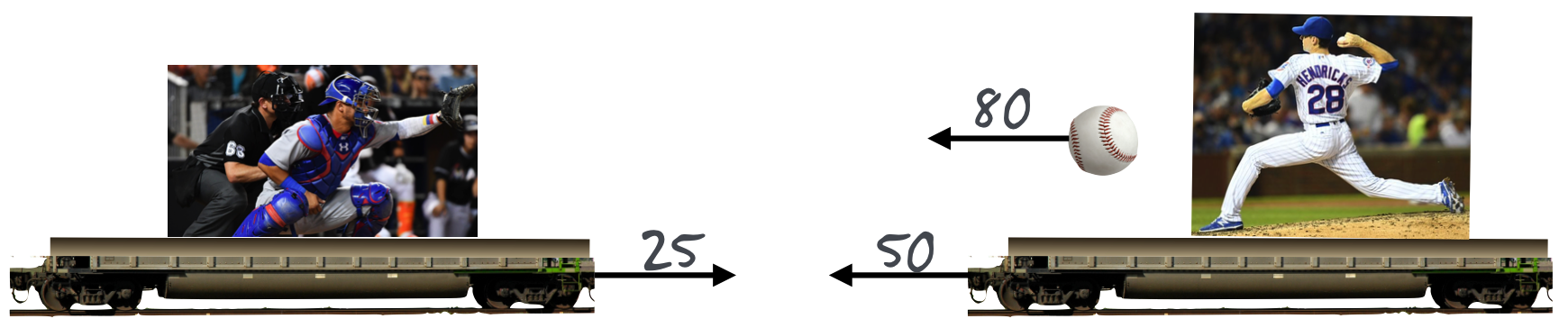
  Okay. Now this is silly. They’re going to collide. But before they do, the speed that the catcher would feel would be \(80+50+25=155\) mph.

  Glad you asked: Yup. Yes, that’s right. Apart from the silliness, it’s exactly what your common sense would suggest.

Note

Now, Hendricks is just messing around, but I’ll bet he took a course at Dartmouth (and I suspect I know the guy who taught him) that included Special Relativity. Instead of a baseball, he’s pitching light. What is the speed of the light beam that Contreras experiences if we’re back to both cars being stationary with respect to the ground and one another?

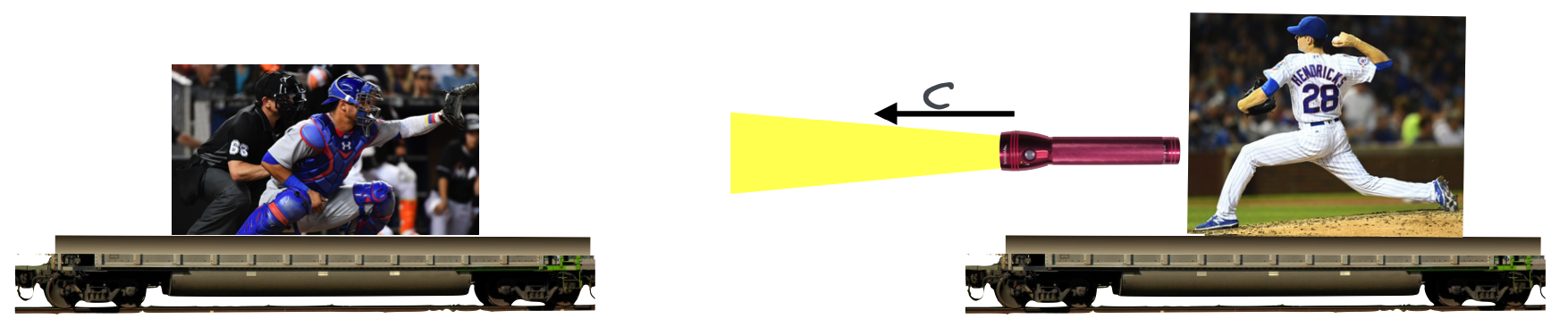
  Okay. It’s \(c\)

  Glad you asked: Just like before.

Note

Now the pitcher’s car is moving towards the catcher at 50 mph and he throws his standard, consistent pitch at 80 mph relative to his car. Now what’s the speed of the light beam that the catcher experiences with Hendrick’s car moving toward the catcher?

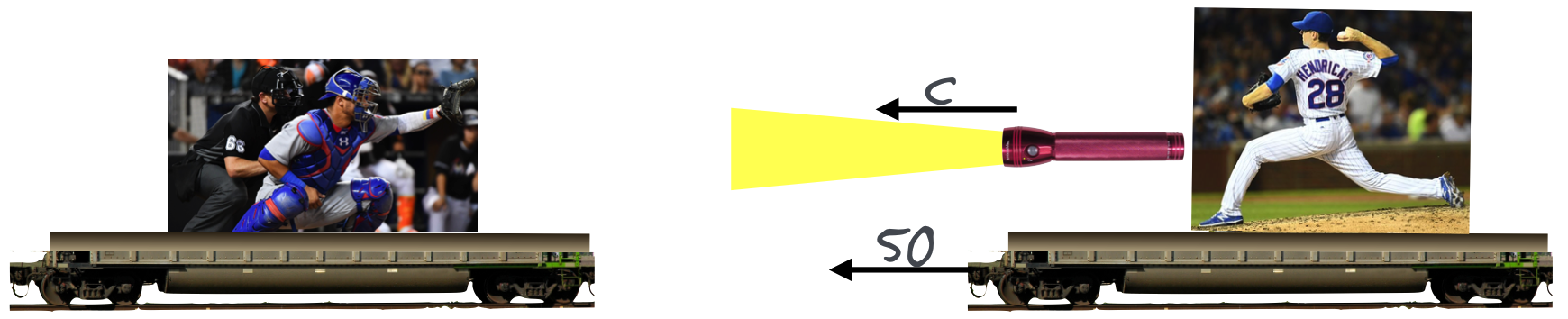
  Okay. I want to say that it’s \(c+50\) mph.

  Glad you asked: Good suggestion. But nope.

The Second Postulate says that regardless of observer’s state of motion, light will always travel at the same speed: \(c=3 \times 10^8\) m/s \(= 186,000\) mph. That same number that Michelson measured over and over.

Note

Now. The catcher’s car is moving toward the pitcher’s car which is still moving at 50 mph. Now. What would the speed of the light beam be that the catcher experienced?

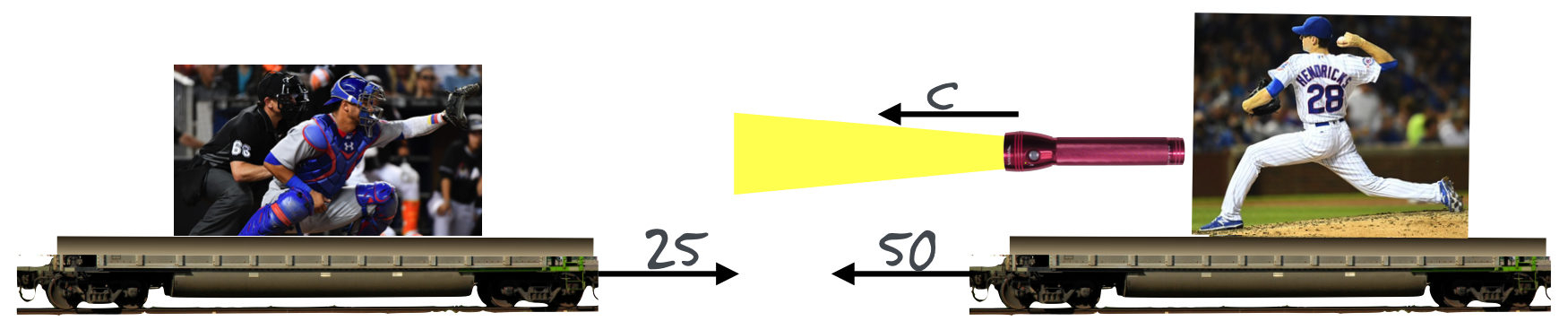
  Okay. I want to say \(c+50+25\) mph but I know you’ll go all “Second Postulate” on me. So I guess I have to say \(c\). Which I don’t like.

  Glad you asked: Neither do I. But you’re right. According to Einstein’s Second Postulate, the speed of the light beam is indeed \(c\).

There are consequences to that Second Postulate. And that “storm” in his mind had to do with the whole idea of how to determine whether events determined to be simultaneous in one inertial frame of reference can be simultaneous in all inertial frames of reference. Because that’s how you “tell the time” of an event.

  Please answer question 1 📺

Pitching light

Back to that remarkable paper:

“Our judgments in which time plays a part are always judgments of simultaneous events,…If, for instance, I say, ‘That train arrives here at 7 o’clock,’ I mean something like this: ‘The pointing of the small hand of my watch to 7 and the arrival of the train are simultaneous events.’”

Note

Simultaneity. That’s the storm.

16.3.1. Simultaneity

Let’s see what the Second Postulate says with the pitching exercise in mind. Another way of describing the odd result is that the light beam did not carry the motion of the source (the pitcher) with it when it made the trip between co-moving frames of reference. That speed was all to itself, independent of everything, and just plain….\(c\).

Keeping our transportation metaphor in mind, let’s do another Einstein-like thought experiment. Here’s the situation:

• We have a fellow lounging on the ground next to a railroad track. “Track man.”

• On a train car is “Train Lady” who has pre-assembled a set of physical circumstances:

  • She has rulers and clocks and a light source for measurement.

  • She lays out a line on her car from left to right and positions her self precisely at the center of the line.

  • At the left and the right edges she’s created light-detectors that can record the time of arrival of a light beam. She needed her light source to set this up so that they are synchronized, like described in Lesson @ref(relativity1).

  • She’s also got a light bulb with her at the center that when she pushes a button, will send out a spherical light front that will then eventually hit her light detectors.

• The thought experiment has two phases:

  • The train car is stationary with respect to the ground, so both Train Lady and Track Man are stationary relative to one another. When she pushes the button what do both of them see the light detectors register?

  • Now the train car moves from left to right at a constant speed. When Train Lady passes in front Track Man, a switch is thrown and the light beam is started from her bulb. This establishes the origin of time that both of them would agree to: \(t_{\text{Train Lady}}=t_{\text{Track Man}}=0\). What do both of them see the light detectors register?

  Let’s see what happens.

Note

Watch how the two observers see the expanding light from a single source. With the Second Postulate running the show.

Because of the Second Postulate:

• The light beam does not carry the motion of the train car with it: both observers see light traveling at \(c\).

• Train Lady says that the light beams hit her detectors at the same time: they are simultaneous in her frame.

• Track Man says that the light beam hits her left detector before her right detector: they are not simultaneous in his frame.

Isn’t this a little strange?

Einstein interpreted the consequence of this thought experiment–remember, having to accept the result if the model’s logic is sound–as requiring that the whole concept of Simultaneity does not exist.

There is no such concept as Simultaneity between co-moving, inertial reference frames.

That means that we’ve got a problem. Two of them, potentially:

1. Since there is no way to determine that an event is simultaneous in one frame and also in another:

   1. One can never synchronize clocks between co-moving, inertial frames of reference – remember his pedantic description of the watch statement above.

   2. So one can never determine the privileged position of any frame being absolutely at rest or a special frame of reference

2. The notion that a cause always precedes an effect seems threatened by this.

Remember the movie The Curious Case of Benjamin Button? Time seemed to go wrong for him. If there is a frame of reference in which A follows B but that sequence can be altered by moving relative to that frame…then could you find a frame in which B appears to a relatively moving observer to follow A?

What if A physically causes B! Now we have a problem for physics since effects really need to come after causes and this simultaneity exercise seems to threaten the very idea of causality.