10.4. What’s the Moon’s Centripetal Acceleration?#
This is an ingenious argument. Follow the example with your pencil out. It’s one of those moments in the history of physics where a monumental discovery is made that’s actually pretty straightforward to understand.
Here is the situation: the Moon orbiting the Earth at a distance of \(D_M\):
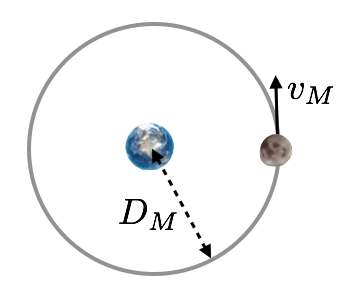
Pens out! 🖋
If it’s executing circular motion, then it has a centripetal acceleration. If it has a centripetal acceleration, then it experiences a centripetal force – his guess is that that centripetal force is due to the Earth pulling on it and if that’s the case, then that centripetal acceleration is the acceleration due to gravity – at the position of the Moon!
Is there any relation between our \(g\) on Earth and the Moon’s centripetal acceleration?
He needed to find the centripetal acceleration of the Moon using what he knows about the Moon’s motion. He knows that it takes about a month to go around the Earth and he knows Kepler’s Third law: \(T^2 \propto D_M^3\). Remember the centripetal acceleration from Lesson @ref(bigmo), here adopted to the figure of the Moon:
How does he actually know the Moon’s speed, \(v_M\)? Well, that’s the easy part. The speed is the distance traveled — the circumference of the Moon’s orbit — divided by the time that it takes to go around, that is its period (1 month), which we’ll call \(T\). So the speed is
which we can substitute into the centripetal acceleration relation, Equation 7.2 to get
Then he used Kepler’s rule from Equation 7.3 to relate the period and the radius:
where I’ve inserted a constant of proportionality, \(k_E\), which is different from Kepler’s value which was for the planets-Sun, not Moon-Earth. Newton picked out the physics idea and applied it in a way that Kepler never intended and inserts a new proportionality constant for the little Earth-Moon system.
Substituting \(T^2 = k_E D_M^3\) for the Moon’s orbit into the denominator of the centripetal acceleration equation gives us:
Stand back and admire this! It’s an historic moment. He’s shown that the centripetal acceleration of the Moon is proportional to the inverse square of the distance from the Earth to the Moon: \(\frac{1}{D_M^2}\).
That means that the force would vary as \(\frac{1}{D_M^2}\) or more generally, \(\frac{1}{R^2}\).
Kepler thought that there was a force from the sun on the planets (magnetic!) and that it diminished as the inverse of the distance from the sun. That whatever the force is might diminish as the inverse of the square of the distance is something that many suspected about the planets, but nobody figured it out before this moment, much less for the Earth-Moon system. Keep it in mind. Newton also showed that if such an orbit (Sun-planets, Earth-Moon, Saturn-Moon!) were a circle, an ellipse, a parabola, or a hyperbola that the force of attraction would have to be? That’s right, \(\frac{1}{R^2}\).
The “inverse-squared law” is a standard thing in physics and we’ll meet it more than once as we move toward the 20th century.
Please study Example 1:
10.4.1. How Newton Confirmed His Model of Gravity#
Here’s one more conceptual leap required. Remember we’re worried about why an apple falls to the Earth. The left of the figure below looks like two entirely different circumstances. One of the core (see what I did there? apple? “core”?) results of his calculus is that all of the gravitational effects of an extended massive sphere are identical to the situation if the mass of that object was concentrated in a point at the center of that original sphere. Let’s shrink the Earth and do one more thing: let’s move the Moon to the original distance from the center previously occupied by the Earth’s surface. The right figure does that with the dashed line denoting the original Earth circumference at a radius \(D_E\).
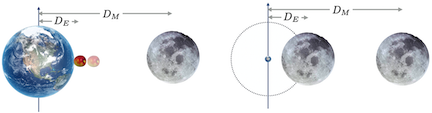
Fig. 10.5 On the left, an apple peacefully falls to the surface and the Moon calmly lives in its orbit. On the right, a fanciful circumstance in which the apple is replaced with a moon orbiting at the Earth’s radius.#
An apple falls, so Newton reasons there’s a force acting on it and he guesses that that force is directed to the center of the Earth. His guess is that the same force that governs the apple’s fall is the one that makes the Moon “fall” and here’s essentially his strategy to test that idea. The “Moon Argument” he called it in Principia. Here’s what he knew about the Moon:
The velocity of the Moon, you figured out in Example 1. It turned out to be \(3.36\times 10^3\) ft/s.
The distance from the Earth to the Moon had been known since the Greeks to be about \(60 \times D_E\) the radius of the Earth. That too had been known fairly well. The modern average number is \(D_E=20,902\) ft.
He’s already shown that the centripetal force of the Moon in its regular orbit: it’s Equation @ref(eq:centripetal) above. This example fleshes out the conclusions that follow.
Please study Example 2:
Pens out!
If we put in modern numbers, we get that the centripetal acceleration of the Moon in its orbit is:
Put on your seatbelt. He asked the absurd question; Suppose he moved the Moon to the radius of the Earth’s surface, what would its centripetal acceleration be? His earlier argument says that it should be larger by the ratio of the square of the distances:
Remember that the acceleration due to gravity—how apples fall—“little \(g\)” is…Trumpets: \(g=32 \text{ ft/s}^2\)! He’s done an amazing thing!
Newton measured the acceleration of gravity on the Earth…by using the Moon!
Think about that.
He’s also shattered whatever pitiful remains are left of Aristotle’s physics. Good riddance.
This is rather remarkable and a brand new idea:
The same physical theories govern motion on Earth and the cosmos.
Please answer Question 1 for points:
Please answer Question 2 for points:
Please answer Question 3 for points: