16.5. Double Down on the Second Postulate

There will be consequences! Here’s a thought-device. A and D are light detection instruments–notice that there are meter sticks enforcing that they are the same distance from the center, C and F are time measuring instruments, and B and E are the connections of the detectors to the time measuring devices. The are both connected by identical, same-length cables.

A clever machine that will precisely measure the time that it takes for light to go from detector A to detector D, which are precisely 1 meter distant from the center of the table. You can see that there are timers at C and F and that the cables from A and D are precisely the same length as they attach to the timers at B and E. Precisely determined cable lengths is really important in electronics and "ringing the cable" is the process of making sure.

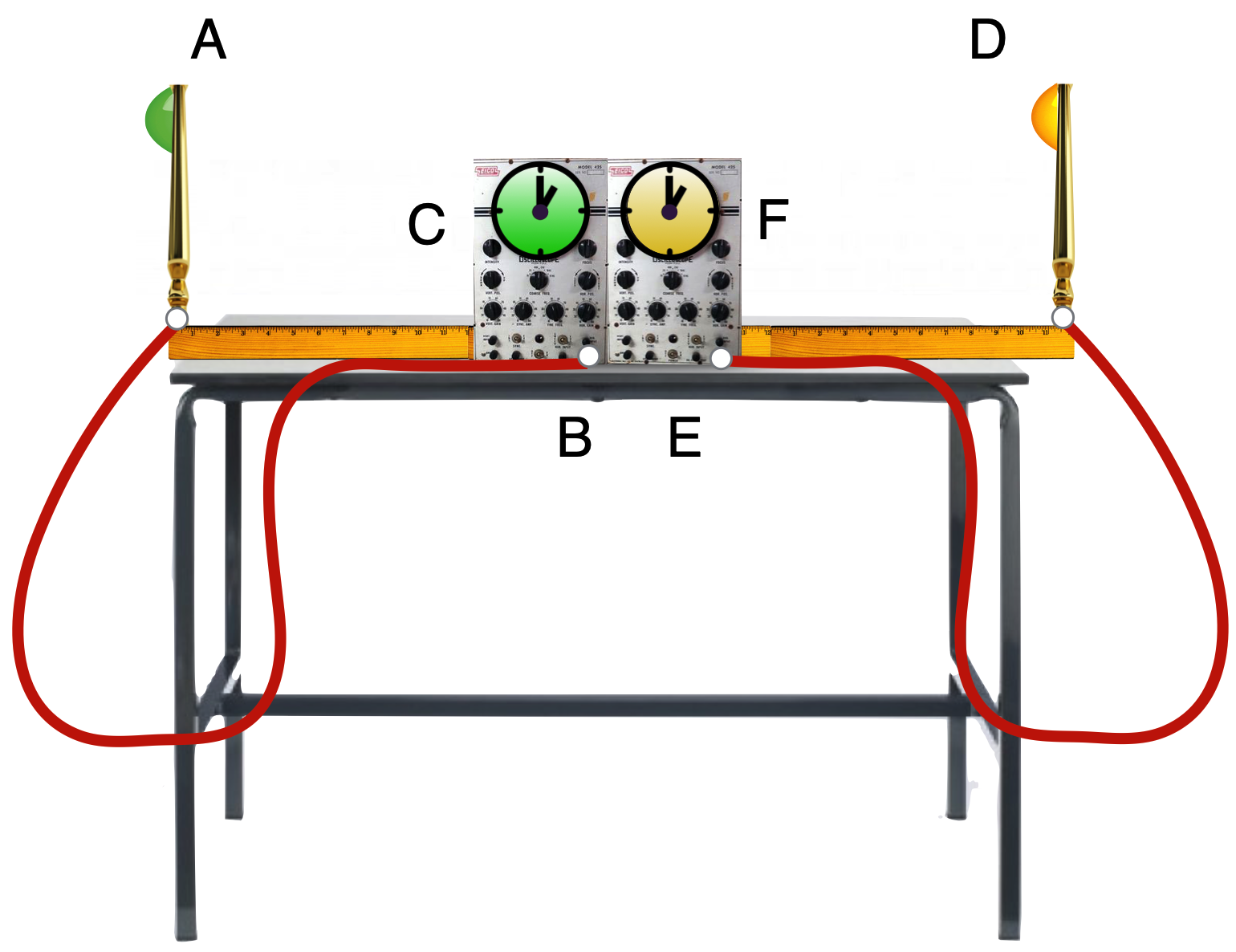
If a beam of light travels from A to D the time that A and D detect the beam can be determined by C and F and knowing the distance between A and D, the speed of light can be measured:

Here' we're taking one of our machines out for a spin with a flashlight aimed at both detectors. You can see that I've calibrated the timers so that C establishes the "$t=0$ time and F registers the time since zero.

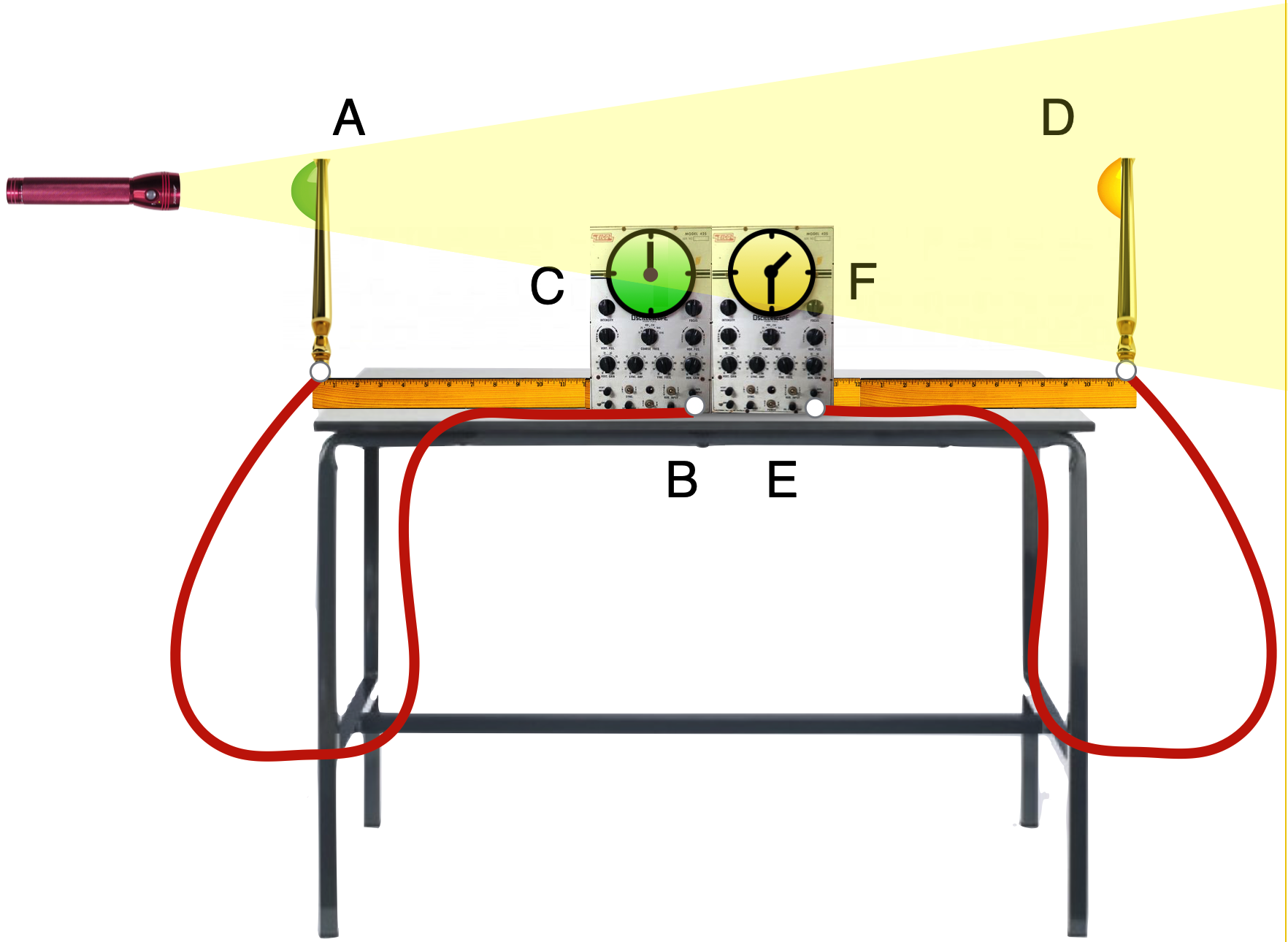
Notice that F has registered the finite time that the light took to go from A to D.

Now let’s build two setups, one for Couch People and one for Sidewalk Guy back at the airport.

Here's the setup. Sidewalk Guy has his machine and Couch People have theirs.

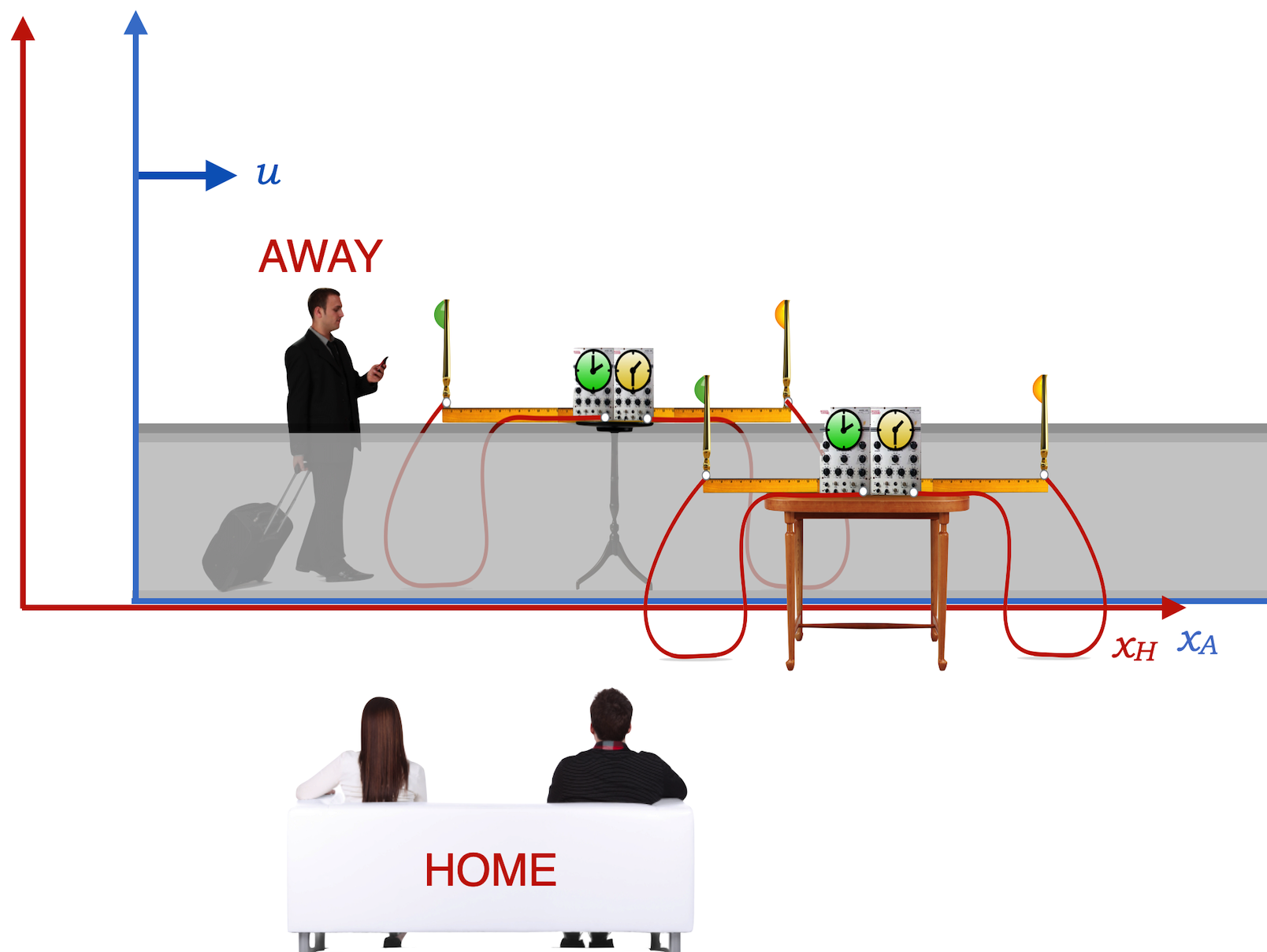
And we’ll fix a light source in the airport and shine it down the concourse so that it intercepts both instruments, the one moving with Sidewalk Guy and the one beside the sidewalk in the Home frame with Couch People.

A light source is shown from the left so that it interacts with both machines. What do you think they record as the speeds?

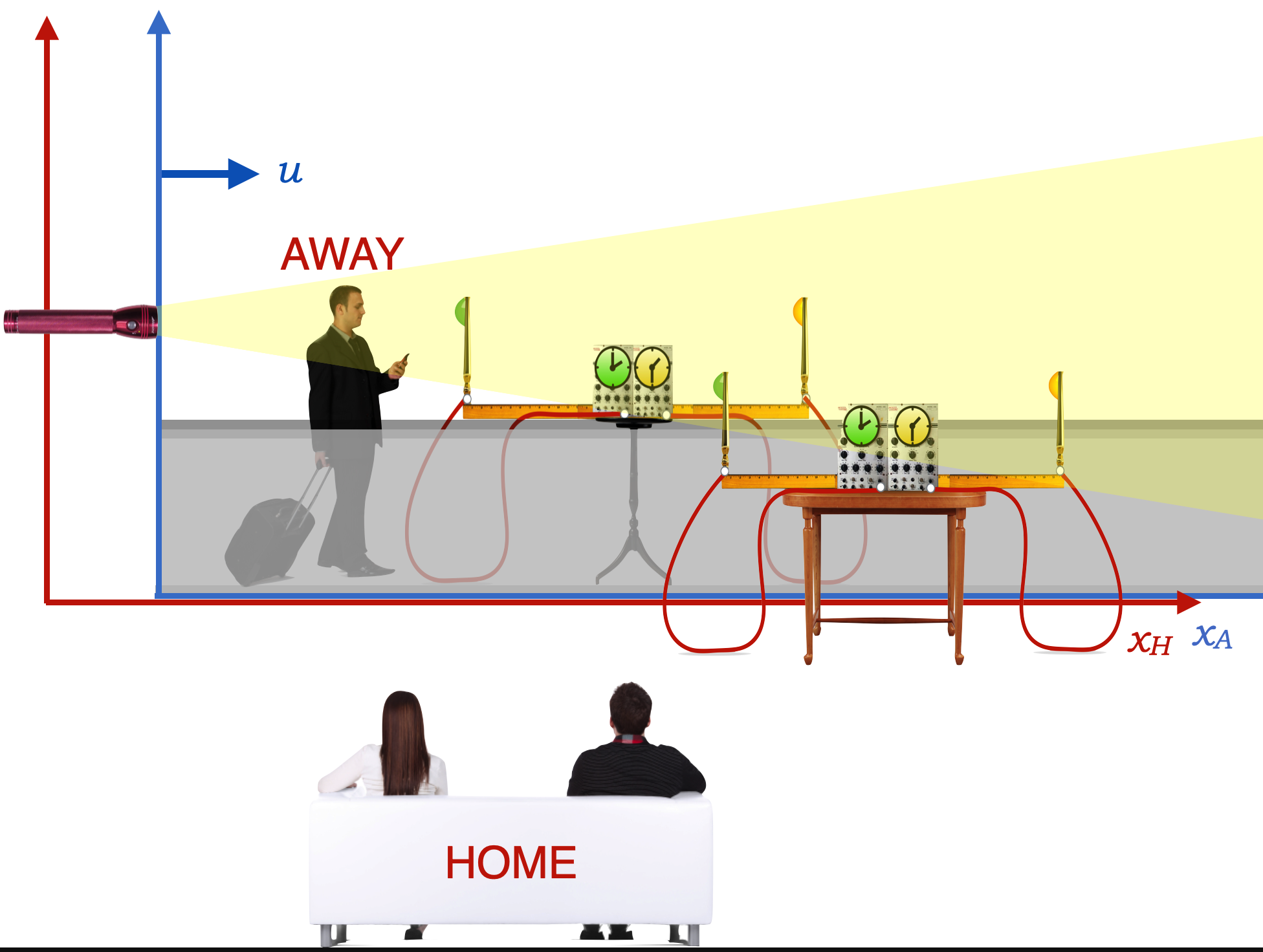
What do the two devices determine for the speed of light in those two apparently different frames of reference?

By now you know:

• Sidewalk Guy’s instrument would record: \(c\)

• Couch People’s instrument would also record: \(c\)

Strange, isn’t it. Obviously, I wouldn’t have led you this far if there wasn’t overwhelming support – dare I say, confirmation – that this bizarre situation isn’t exactly what nature does. Before I get to the evidence, let’s work out what some of the practical ramifications are by specifically following the Second Postulate – that absolutely invariant quantity of \(c\) – to it’s forced conclusions. In the rest of this lesson we’ll consider:

• The behavior of inertial co-moving clocks

• The behavior of inertial co-moving meter sticks

In the subsequent lessons we’ll add to this by considering:

• The behavior of speeds in an away frame as determined by co-moving, inertial observers

• The consequences for space travel

• The consequences for what energy is (the T-shirt equation)