The Cosmologies of Galileo and Newton

The Cosmologies of Galileo and Newton#

Example 3: An apple of my eye…litte \(g\) and big \(G\)#

The Question:

Place your apple on the ground—notice that it’s distance from the center of the Earth is \(R_E\). Let’s calculate the force on that little apple with mass \(m\) due to the big Earth, with mass \(M_E\). Here’s a picture:

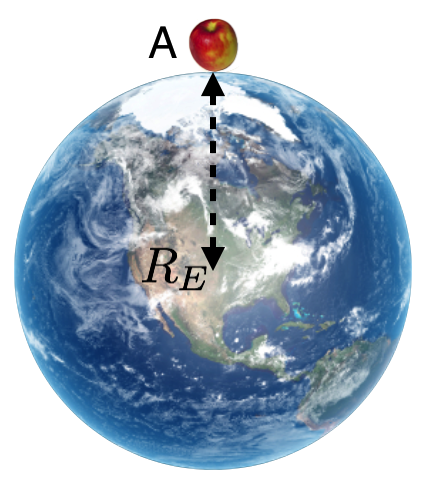
../../_images/appleearth1.png

The Answer:

Newton taught us that the force between them is from Newton’s Gravitational law

\[ F = G\cfrac{M_Em}{R_E^2}. \]

Now isolate the little m outside of the other terms:

\[ F = m\left(G\cfrac{M_E}{R_E^2}\right)=ma \nonumber \]

and can you see that we’ve discovered an acceleration buried in the middle term by recognizing \(F=ma\) in it:

\[ a = G\cfrac{M_E}{R_E^2}. \]

Since this situation is an apple on the surface of the Earth, what we’ve really found is a derivation for Galileo’s \(g\)! So we can just identify:

()#\[ g = G\cfrac{M_E}{R_E^2}. \]

All constants. Try it:

  • \(M_E=5.972 \times 10^{24} \) kg

  • \(R_E= 6378 \times 10^3 \) m

  • \(G=6.67 \times 10^{-11} \) m\(^3 \)kg\(^{-1} \)m\(^{-2}\)

\[ g = G\frac{M_E}{R_E^2}=\left( 6.67 \times 10^{-11} \right) \frac{5.972 \times 10^{24}}{ (6378 \times 10^3)^2} = 9.79 \text{ m/s}^2 \]

Bingo.

Contents