Relativity 2

Relativity 2#

Example 1: The Decay of an Elementary Particle#

The Question: There are only three kinds of elementary particles that appear to be absolutely stable. We’re made of electrons, protons, and neutrons, right? Neutrons by themselves don’t hang around very long – a 100 neutrons will become 50 neutrons in about 15 minutes! Think of it. One moment a neutron is minding its own business and quite randomly, it suddenly becomes a proton, and electron, and the strange elusive particle called a neutrino.

Although our theories do suggest that protons might decay, all attempts to confirm that have not seen it yet. The lifetime of a proton is more than \(10^{34}\) years, which is impressive since the age of the universe is about \(10^{10}\) years. Likewise, theories can accommodate an unstable electron, but searches for that possibility lead to a lifetime that’s more than \(10^{28}\) years. Lucky for us, as our bodily atoms decaying around us would be a disappointment.

One unstable particle that we’ll learn about is called the “pion” (”\(\pi\)”) and it decays into another unstable particle called a “muon” (”\(\mu\)”) which in turn, decays into an electron. The lifetime of a pion is about \(2.5 \times 10^{-8}\) seconds…25 nanoseconds. They are readily produced in cosmic rays and artificially in accelerators. So let’s do that.

The scenario:

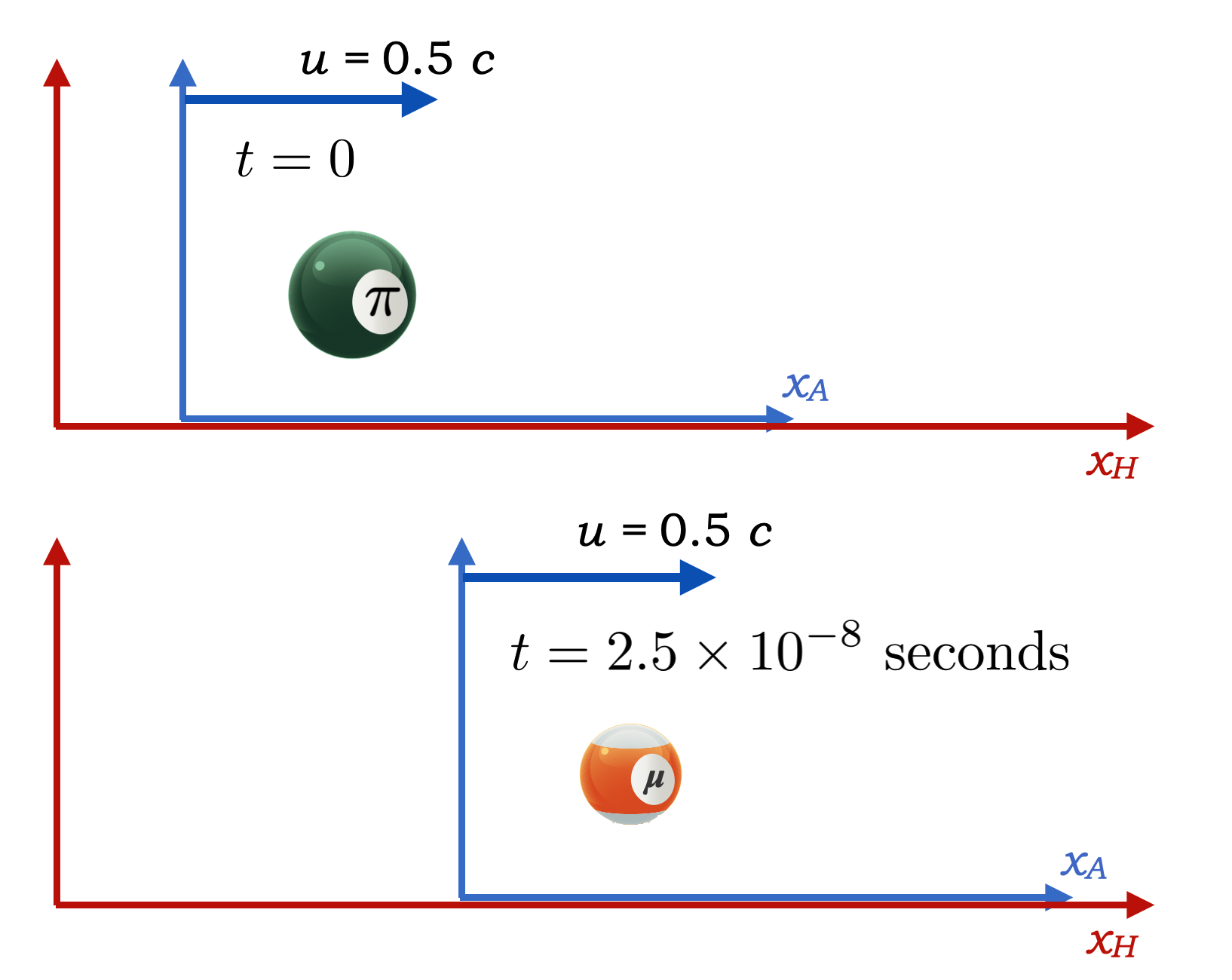
  • A pion is produced in an accelerator and moves away from its place of birth at a speed of half that of light. The pion is itself its own rest frame (the “proper frame”)

  • The lab in which it was produced is where we are observing. So the lab is Home and the pion’s frame is Away and is moving at \(u=0.5c\).

  • The pion decays into a muon after one of it’s lifetimes of \(2.5 \times 10^{-8}\) seconds. So we have a distinct interval: the pion is born and then the pion decays. It’s a little clock with one “tick” and never a “tock.”

How long does the pion appear to live as observed in the lab, Home, frame?

galilean_train

The Answer:

This is a very standard example of time dilation. In our language now:

  • \(t_A = 2.5 \times 10^{-8}\) seconds

  • \(u=0.5c\)

  • \(t_H\) is what we want to determine.

From the time dilation model we know that:

\(t_H = \gamma t_A\)

so we need to know what \(\gamma\) is which we can get from the graphs in the text.

\(\beta = 0.5\) gives \(\gamma = 1.154\)

so the time that the pion lives in the laboratory is

\[\begin{split} \begin{align*} t_H &= \gamma t_A \\ &= 1.154 \times 2.5 \times 10^{-8} \\ t_H &= 2.9 \times 10^{-8} \text{ seconds} \end{align*} \end{split}\]

The pion appears to live longer to us than it does to the pion itself.

Contents